Правило знаків: якщо ординати, що перемножуються, одного знака (лежать по одну сторону), одержуваний добуток позитивний, якщо знаки ординат різні - добуток негативний

Результат обчислень позитивний, якщо напрямок одиничного навантаження збігається з напрямком дійсного переміщення, і негативний, якщо напрямок одиничного навантаження не збігається з напрямком дійсного переміщення.

Порядок визначення переміщень за допомогою інтеграла Максвелла-Мора.

1. Прикладаємо зовнішнє навантаження, визначаємо опорні реакції, розбиваємо балку на ділянки, записуємо вирази (функції) згинаючого моменту 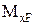для кожної ділянки.

2. У точці, переміщення якої визначаємо, прикладаємо:

a) одиничну силу при визначенні прогину (лінійного переміщення);

b) одиничний момент при визначенні кутового переміщення.

Визначаємо опорні реакції й у такому ж порядку, як і для зовнішнього навантаження, на кожній ділянці записуємо вирази (функції) згинаючого моменту .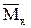

3. Підставляємо функції (вирази) 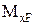і 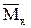в інтеграл Максвелла-Мора та робимо відповідні обчислення.

Приклад 2. Консольна балка постійного поперечного перерізу (ЕI_x=const) довжиною 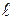навантажена на кінці зосередженою силою 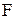(рис.8.4а). Визначити прогин 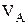та кут 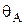повороту на кінці консолі.

Рис. 8.4.

1. Запишемо функцію 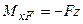(рис.8.4а).

2. У точці 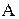прикладаємо одиничну силу (рис.8.4б) та записуємо функцію .

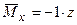3. Підставляюч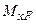и й 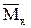в інтеграл, одержимо: 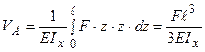(див. приклад 1 на рис. 8.2).

4. Для визначення кутового переміщення у точці 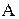прикладаємо одиничний момент (рис.8.4в) та записуємо функцію .

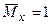5. Підставляюч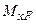и й 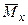в інтеграл, одержимо: .

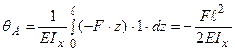Результат обчислення прогину 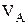позитивний, тому що прикладена одинична сила збігається з напрямком дійсного переміщення. Результат обчислення кута повороту 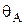негативний, тому що прикладений одиничний момент по напрямку не збігається з дійсним напрямком кута повороту перерізу в точці .

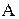Спосіб перемножування епюр. Правило Верещагіна.

1. Обчислення інтегралів Мора істотно спрощується, якщо одна з епюр (у дійсному чи одиночному стані) прямолінійна. Ця умова виконується для систем, що складаються з прямих стержнів, оскільки при цьому епюра внутрішніх сил від одиничного навантаження (зосередженої сили або пари сил) завжди обмежена прямими лініями.

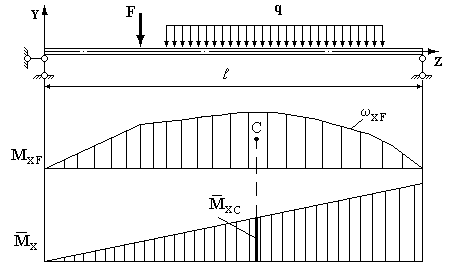
Рис. 8.5.

2. Обчислимо інтеграл Мора для випадку, коли епюра 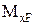від заданого навантаження має довільну форму, а від одиничного 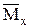-прямолінійну (рис. 8.5).

Використовуючи геометричну інтерпретацію визначення інтегралу як значення площі, інтеграл Мора для визначення переміщень у балках постійного перерізу можна обчислити за допомогою спеціальної операції над епюрами відповідних згинальних моментів.

В результаті одержимо наступне:

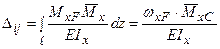, (8.6)

де 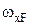- площа вантажної (від зовнішнього навантаження) епюри 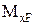; 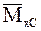- ордината, узята з одиничної епюри 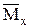під центром ваги 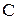вантажної епюри .

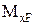Правило знаків. Якщо епюри, що перемножуються, лежать по один бік (обидві нагорі або внизу), добуток додатний; якщо епюри, що перемножуються, лежать по різні боки - добуток від¢ємний.

Якщо епюра від зовнішнього навантаження кусочно-лінійна на ділянках, а одинична епюра завжди кусочно-лінійна, результат перемножування не залежить від порядку використання співмножників, тобто:

, (8.7)

де 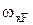- площа епюри від зовнішнього навантаження; 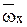- площа епюри від одиничного навантаження; 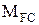- ордината під центром ваги одиничної 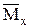епюри, узята з епюри 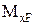від зовнішнього навантаження.

Якщо епюри 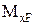і 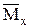складаються з декількох ділянок, то перемножування здійснюється по ділянках, а результат підсумовується, тобто:

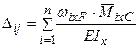. (8.8)

Відзначимо, що в розглянутих задачах епюри вантажних та одиничних згинальних моментів складаються з досить простих площ: прямокутник, трикутник, параболічний трикутник і т.д. У таблиці приведені площі w та координати центрів ваги z_c плоских фігур, що зустрічаються в епюрах.

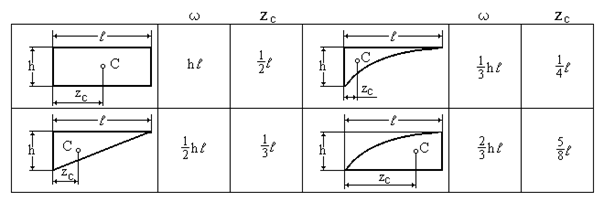
При рішенні конкретних задач доцільно використовувати правило трапеції для перемножування лінійних епюр і правило Симпсона-Карнаухова для перемножування будь-яких епюр (у більшості випадків нелінійних).

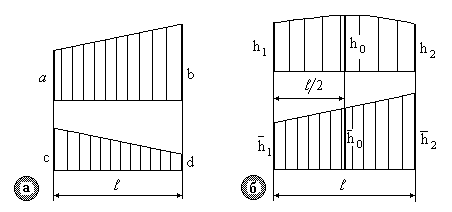
Рис.8.6.

Правило трапеції (тільки для лінійних епюр – рис.8.6а). У тому випадку, коли на ділянці епюра 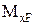від зовнішнього навантаження лінійна, перемножування епюр можна виконати за правилом трапеції. Результат перемножування лінійних епюр на ділянці довжиною 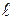дорівнює:

.

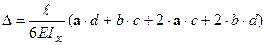Правило Симпсона - Карнаухова (для лінійних епюр і епюр, описуваних квадратною параболою-рис.8.6б). Результат добутку наступний:

.

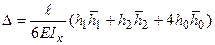Тут 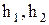- крайні ординати вантажної епюри (нелінійної) на ділянці; 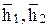- крайні ординати одиничної епюри (лінійної) на ділянц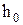і; і 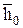- середні ординати епюр на ділянці. Правило знаків при перемножуванні ординат аналогічно правилу трапеції.

Приклад 3. Для консольної балки, навантаженої зовнішніми силами, як показано на рис.8.7, визначити прогин та кут повороту на кінці консолі в перерізі .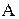

1.Визначаємо опорні реакції.

; .

; .

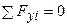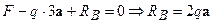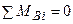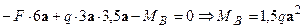Перевірка: .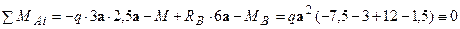

2.Записуємо вирази 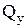і 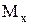, будуємо відповідні епюри.

: ; .

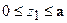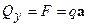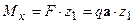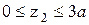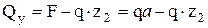: . Поперечна сила змінює знак при .

.

; .

: ; .

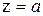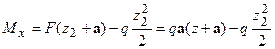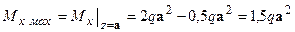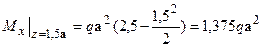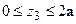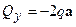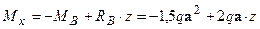3.У точці 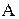прикладаємо одиничну силу, будуємо епюру 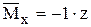, визначаючи ординати на границях кожної ділянки.

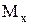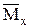4.Перемножуючи епюри і , визначаємо шуканий прогин:

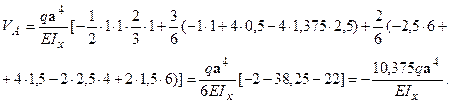
Тут на першій ділянці перемножування епюр виконано за правилом Верещагіна; на другій - Симпсона, на третій - трапеції. Знак мінус указує на те, що під дією зовнішнього навантаження переріз переміщується уверх.

5.У точці 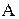прикладаємо одиничний момент, будуємо епюру 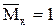. Перемножуючи її по ділянках з вантажною епюрою, визначаємо кут повороту перерізу .

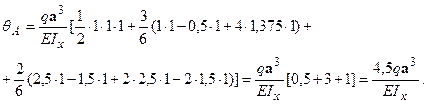
Тут на першій ділянці перемножування виконане за правилом Верещагіна, на другій - Симпсона, на третій - трапеції. Результат обчислень позитивний, отже, напрямок кута повороту перерізу збігається з напрямком одиничного моменту.

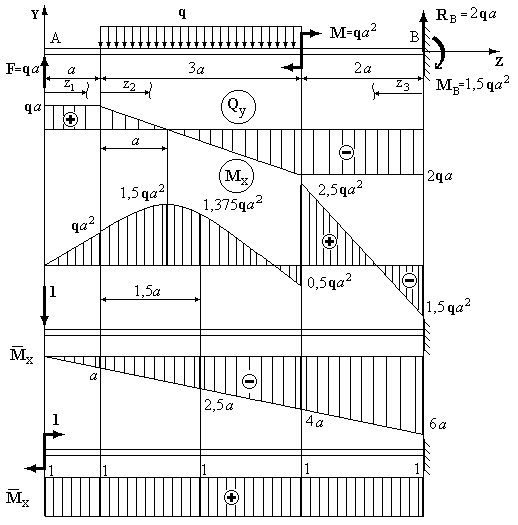
Рис.8.7.

КОНТРОЛЬНІ ПИТАННЯ

1. Що називається пружною лінією балки?

2. Що називається прогином балки і кутом повороту перетину?

3. Що називається жорсткістю при вигині?

4. Як записується диференціальне рівняння пружної лінії?

5. З яких умов визначається рівняння кутів повороту?

6. Як виходить з рівняння пружної лінії в диференціальній формі рівняння пружної лінії, що дає безпосередній зв'язок між прогином 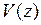і абсцисою ?

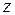7. Чому дорівнює прогин консольної балки під дією сили, що прикладена на вільному кінці?

8. Чому рівний прогин балки, яка вільно лежить на двох опорах і навантажена силою посередині прольоту?

9. Яка балка називається балкою рівного опору вигину?

10. Який порядок визначення лінійних і кутових переміщень за допомогою інтеграла Максвелла-Мора?

11. В чим полягає сенс визначення переміщень за допомогою ПРАВИЛА ВЕРЕЩАГІНА? Яке правило знаків?

12. Напишіть порядок перемножування епюр за допомогою ПРАВИЛА ТРАПЕЦІЇ. Яке правило знаків?

13. Для перемножування яких епюр застосовується ПРАВИЛО ТРАПЕЦІЇ?

14. Напишіть порядок перемножування епюр за допомогою правила СІМПСОНА-КАРНАУХОВА. Яке правило знаків?

15. В чим полягає сенс розрахунків на жорсткість при вигині?

Дата добавления: 2015-06-28