Проектирование монолитного перекрытия

Примеры проектирования железобетонных конструкций

  Рис. 1. Совместный план монолитного и сборного перекрытий.

Монолитное перекрытие компонуем с поперечными главными балками и продольными второстепенными. Второстепенные балки размещаем по осям колонн в половине пролёта главной балки, при этом пролёт плиты между осями рёбер равен:

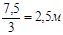
Предварительно задаёмся размерами сечений балок:

- главная балка:

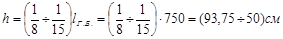
принимаем ;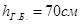

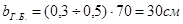
- второстепенная балка:

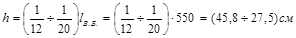
принимаем ;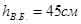

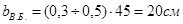
т.е. размеры сечений второстепенной и главной балок приняты равными

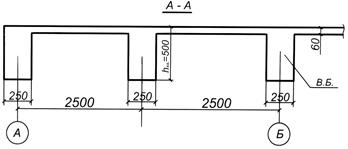
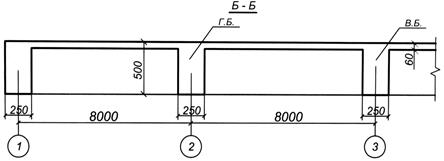Рис. 2. Сечение монолитного перекрытия.

6.3.1.1. Расчёт многопролётной плиты

Расчётный пролёт и нагрузки.

Расчётный пролёт плиты равен расстоянию в свету между гранями рёбер 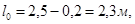в продольном направлении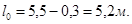

Отношение пролётов 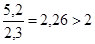- плиту рассчитываем, как работающую по короткому направлению. Толщину плиты принимаем 6 см.

Нагрузки на 1 м² перекрытия:

Таблица 5.

Нагрузка	Нормативная нагрузка Н/м^2	Коэффициент надёжности по нагрузке, gf	Расчётная нагрузка Н/м^2
1. Постоянная:
- от собственного веса плиты s = 60 мм; r = 2500 кг/м^3 (0,06´1,0´25000 = 1500 Н/м^2)		1,1
- от слоя цементного раствора s = 20 мм; r = 2200 кг/м^3 (0,02´1,0´22000 = 440 Н/м^2)		1,3
- от керамических плиток s = 13 мм; r = 1800 кг/м^3 (0,013´1,0´18000 = 230 Н/м^2)		1,1
Итого: g
2. Временная нагрузка, v:		1,2

Полная расчётная нагрузка

q = g + v = 2477 + 5160 = 7637 Н/м².

Для расчёта многопролётной плиты выделяем полосу шириной 1 м, при этом расчётная нагрузка на 1 м длины плиты равна 7637 Н/м².

С учётом коэффициента надёжности по назначению здания

g_n = 1, нагрузка на 1 м равна 7637×1 = 7637 Н/м.

Изгибающие моменты определяем как для многопролётной плиты с учётом перераспределения моментов:

- в средних пролётах и на средних опорах:

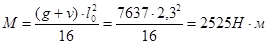
- в первом пролёте и на первой промежуточной опоре:

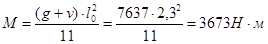
Средние пролёты плиты окаймлены по всему контуру монолитно связанными с ними балками и под влиянием возникающих распоров изгибающие моменты уменьшаются на 20%, если .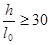

При 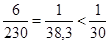– условие не соблюдается.

Характеристики прочности бетона и арматуры.

Бетон тяжёлый класса B25; призменная прочность R_b =14,5 МПа, прочность при осевом растяжении R_bt =1,05 МПа. Коэффициенты условий работы бетона g_b2 = 0,9

Арматура – проволока класса Вр500 диаметром 5 мм в сварной рулонной сетке, R_s = 415 МПа.

Подбор сечений продольной арматуры.

В средних пролётах и на средних опорах

h₀ = h – a = 6 – 2,25 = 3,75 см.

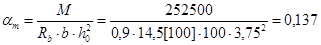
По таблице 3.1[1] находим значение z = 0,926

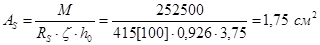
Принимаем 7Æ6 Вр500 c A_S = 1,98 см² и соответствующую рулонную сетку (с-1) 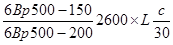(в пролёте 5,5 м укладывается три сетки).

В первом пролёте и на первой промежуточной опоре

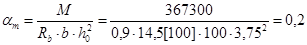
По таблице 3.1[1] находим значение z = 0,887

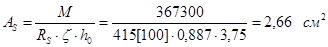
Принимаем две сетки с общим числом стержней 11Æ6 Вр500 c A_S = 3,113 см²

(с-1) 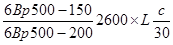и (с-2)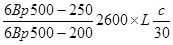

6.3.1.2. Расчёт второстепенной балки

Расчётный пролёт и нагрузки.

Расчётный пролёт равен расстоянию в свету между главными балками: l₀ = 5,5 – 0,3 = 5,2 м.

Расчётные нагрузки на один метр длинны:

- постоянная:

собственный вес плиты и полок: 2,477×2,5 = 6,2 кН/м. то же, балки сечением (0,2´0,45) м, r = 25000 Н/м³;

g_f = 1,1; 0,2×0,45×25000×1,1 = 3438 Н/м = 3,44 кН/м

с учётом g_n = 1: g = (6,2 + 3,44)×1 = 9,64 кН/м.

- временная:

с учётом g_n = 1: v = 5,16×2,5×1 = 12,9 кН/м.

- полная нагрузка:

q = g + v = 9,64 +12,9 = 22,54 кН/м.

Расчётные усилия.

Изгибающие моменты определяем как для многопролётной балки с учётом перераспределения усилий.

В первом пролёте:

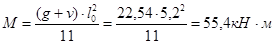
На первой промежуточной опоре:

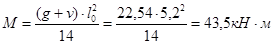
В средних пролётах и на средних опорах:

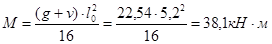
Отрицательные моменты в средних пролётах определяются по огибающей эпюре моментов; они зависят от отношения временной нагрузки к постоянной v/g. В расчётном сечении в месте обрыва надопорной арматуры отрицательный момент при 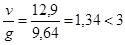можно принять равным 40% момента на первой промежуточной опоре, тогда:

- отрицательный момент в среднем пролёте:

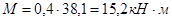
Поперечные силы:

- на крайней опоре

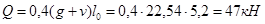
- на первой промежуточной опоре слева

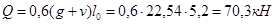
- на первой промежуточной опоре справа

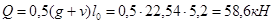
Характеристики прочности бетона и арматуры.

Бетон, как и для плиты, класса В25.

Арматура продольная класса A400 с R_s = 355 МПа; поперечная – класса A240 c R_sw = 170 МПа.

Определение высоты сечения балки.

Высоту сечения балки подбираем по опорному моменту при x = 0,35, т.к. на опоре момент определён с учётом образования пластического шарнира. При x = 0,35 a_m = 0,289. На опоре момент отрицательный – полка ребра в растянутой зоне, сечение работает как прямоугольное с шириной ребра b = 20 см.

Вычисляем

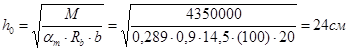
h = h₀ + a = 24 + 4 = 28 см

Принимаем h = 45 см, как принятое ранее.

h₀ = 45 – 4 = 41 см.

В пролётах сечение тавровое – полка в сжатой зоне. Расчётная ширина полки при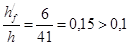

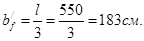
Расчёт прочности по сечениям, нормальным к продольной оси.

а) Сечение в первом пролёте M = 55,4 кН×м.

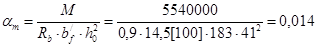
При x = 0,014; a_m = 0,014; -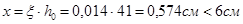

- нейтральная ось проходит в сжатой полке; x = 0,993

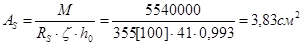
Принимаем 2Æ16 A400 c A_S = 4,02 см².

б) Сечение в среднем пролёте M = 38,1 кН×м.

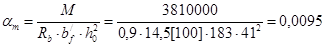
При a_m = 0,01; x = 0,995;

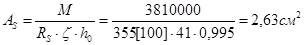
Принимаем 2Æ14 A400 c A_S = 3,08 см².

в) На отрицательный момент M = 15,2 кН×м, сечение работает как прямоугольное.

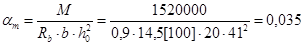
При a_m = 0,035; x = 0,983;

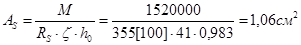
Принимаем 2Æ10 A400 c A_S = 1,57 см².

г) Сечение на первой промежуточной опоре M = 43,5 кН×м. Сечение работает как прямоугольное.

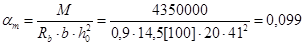
При a_m = 0,099; x = 0,947;

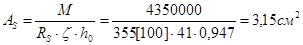
Принимаем 6Æ10 A400 c A_S = 4,71 см² – две гнутые сетки по 3Æ10 A400 в каждой (две сетки С-3).

д) Сечение на средних опорах M = 38,1 кН×м.

При a_m = 0,087; x = 0,954;

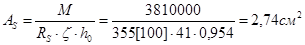
Принимаем 5Æ10 A400 с А_S = 3,93 см две гнутые сетки Æ10 A400 (С-3) и 2Æ10 A400 (С-4).

Расчёт прочности второстепенной балки по сечениям,

наклонным к продольной оси.

Q = 70,3 кН.

Диаметр поперечных стержней устанавливаем из условия сварки с продольными стержнями d = 22 мм и принимаем Æ6 А300, R_sw= 215 МПа. Число каркасов – два; A_sw = 2×0,283 = 0,566 см². Шаг поперечных стержней по конструктивным условиям на приопорных участках 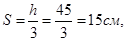принимаем S = 15 см; в пролётной части 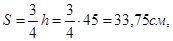принимаем 35 см < 50 см.

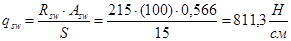
Влияние свесов полки:

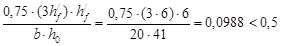
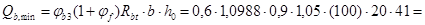
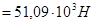
Условие:

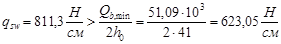– удовлетворяется

Требование:

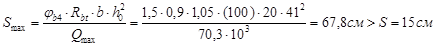– удовлетворяется.

=

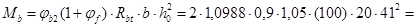
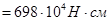
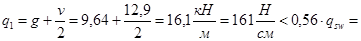
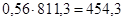
В связи с этим

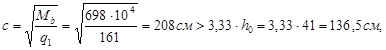
принимаем с = 136,5 см.

Тогда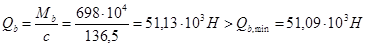

Поперечная сила в вершине наклонного сечения:

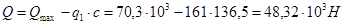
Длина проекции расчётного наклонного сечения

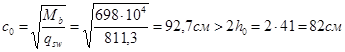
Принимаем с₀ = 82 см.

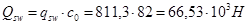
Условие прочности обеспечено:

Проверка по сжатой наклонной полосе:

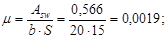
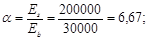
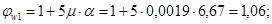
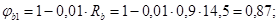
Условие

Q = 70,3×10³ < 0,3 × j_w1 × j_b1 × R_b ×b × h₀ =0,3×1,06×0,87×0,9×14,5×(100)×20×41= = 296×10³ Н – удовлетворяется

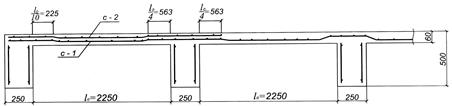  Рис. 3. Схема армирования плиты.

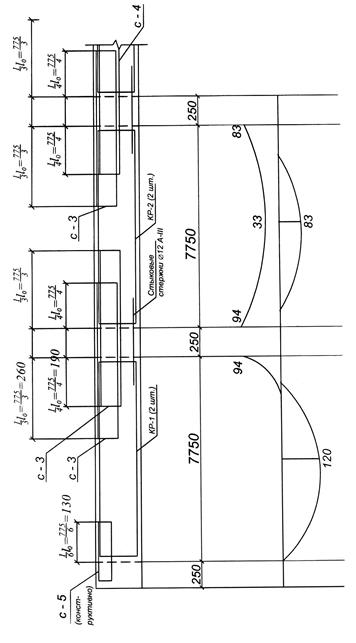Рис. 4. Схема армирования второстепенной балки. Эпюра М.

Дата добавления: 2015-06-29