Ускорение Кориолиса

ускорение Кориолиса равно удвоенному векторному произведению угловой скорости переносного движения на линейную скорость относительного движения.

На основании определения векторного произведения из формулы 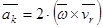можно получить модуль ускорения Кориолиса:

.

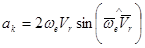Для определения направления ускорения Кориолиса нужно мысленно перенести параллельно самому себе вектор 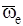в рассматриваемую точки и использовать правило векторного произведения:

· ,

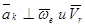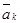· направлено в ту сторону, чтобы глядя с его конца, поворот от 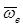к 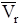был виден против хода часовой стрелки.

Можно искать ускорение Кориолиса и по правилу Жуковского:

Модуль ускорения Кориолиса равен удвоенному произведению угловой скорости переносного вращения на модуль проекции относительной скорости на плоскость, перпендикулярную оси переносного вращения; чтобы получить направление ускорения Кориолиса, необходимо вектор проекции относительной скорости повернуть на 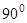вокруг оси, параллельной оси переносного вращения в направлении этого вращения.

Найдем условия отсутствия ускорения Кориолиса ():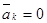

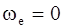· – угловая переносная скорость равна нулю в данный момент времени или переносное движение поступательное;

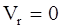· – относительная скорость равна нулю в данный момент времени (точки не перемещается относительно подвижной системы координат в данный момент времени – относительный покой);

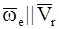· – относительное движение точки в данный момент времени происходит по направлению, параллельному оси вращения переносного движения.

Сложное движение тела (сложение движений твердого тела)

Определение: Движение тела, рассматриваемое одновременно относительно нескольких систем координат называется сложным движением.

Иначе говоря, сложным движением тела называется такое движение тела, которое может рассматриваться состоящим из нескольких движений.

При рассмотрении сложного движения тела, как и в случае сложного движения точки, оказывается удобным классифицировать движения тела на абсолютное, относительное и переносное, введя аналогичным способом неподвижную и подвижную системы координат.

Определение: Абсолютным движением тела называется движение тела относительно неподвижной системы координат.

Определение: Относительным движением тела называется движение тела относительно подвижной системы координат.

Определение: Переносным движением тела называется движение тела вместе с подвижной системой координат относительно неподвижной системы координат.

В этом разделе рассматриваются способы нахождения для данного момента времени распределения скоростей точки, принадлежащих тела, соответствующие сложному движению тела при различных частных случаях относительного и переносного движений тела.

Дата добавления: 2014-01-03