Метод золотого сечения

Метод касательных отличается от предыдущего метода в том, что на k-ой итерации вместо хорды проводится касательная к кривой при и ищется точка пересечения касательной с осью ОХ. При этом не обязательно задавать отрезок [a,b], а лишь достаточно найти некоторое начальное приближение корня. Уравнения касательной, проведенной к кривой в точке с координатами и имеет вид:.

Метод хорд

Так же как и в методе бисекции для функции F(x) уточняется интервал [a;b], на концах которого функция принимает разные знаки. Очередное приближение в отличие от метода бисекции берется в точке , где пересекает ось абсцисс прямая линия, проведенная через точки f(a) и f(b) (рис. 2)

Рисунок 2. Метод хорд.

В качестве нового интервала для продолжения итерационного процесса выбираем тот из двух ([a,x₁], [x₁,b]), на концах которого функция f(x) принимает значения с разными знаками.

Заканчиваем процесс, когда расстояние между очередными приближениями станет меньше заданной погрешности .

.

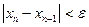Уравнение прямой линии, проходящей через точки и имеет вид: .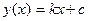

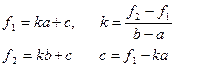
Точку пересечения прямой с осью ОХ получим, приравнивая y(x) нулю:

или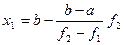

Метод Ньютона (метод касательных)

Отсюда найдем приближение корня с как абсциссу точки пересечения касательной с осью х:

.

Аналогично могут быть найдены и другие приближения:

Методы поиска экстремума функции

Идея метода состоит в использовании на каждой итерации для сокращения интервала неопределенности одной из внутренних точек предыдущей итерации. Должны быть выполнены условия:

- Пробные точки на каждой итерации находятся на одинаковых расстояниях от концов интервала неопределенности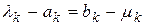

- Для новой итерации точки выбираются так, чтобы 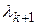совпало с либо 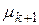совпало с .

- Сжатие интервала неопределенности осуществляется на каждой итерации с одним и тем же коэффициентом сжатия t, удовлетворяющее уравнению . Золотое сечение можно вычислить как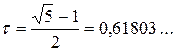

- При выполнении этих условий и вычисляют по формулам

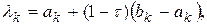(1)

здесь , определяется из условий выше.

АЛГОРИТМ

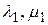Шаг 0. Задать e >0, , k =1. Вычислить по формулам (1),

,

Шаг 1. если 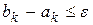, то и 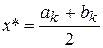конец.

Иначе: если 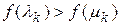, то перейти на шаг 2, если ,

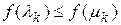то перейти на шаг 3.

Шаг 2. Положить , ,

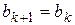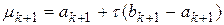, вычислить 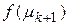, перейти на шаг 4.

Шаг 3 Положить , ,

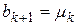, вычислить 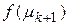, перейти на шаг 4.

Шаг 4. 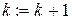переходим на шаг 1.

Если исходный интервал имеет единичную длину, длина интервала после N вычислений равна , иначе 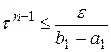. Для достижения точности потребуется итераций.

Дата добавления: 2017-01-14