Метод Симпсона

Методы трапеций

Методы прямоугольников

Метод Эйлера

Пусть дана задача Коши для уравнения первого порядка

где функция определена на некоторой области . Решение ищется на интервале . На этом интервале введем узлы

Приближенное решение в узлах 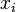, которое обозначим через 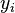определяется по формуле

Эти формулы обобщаются на случай систем обыкновенных дифференциальных уравнений.

Численное интегрирование

Равномерную сетку можно описать следующим набором формул:

где — шаг сетки.

Для равномерных сеток формулы прямоугольников можно записать в виде следующих формул Котеса:

1. Составная формула левых прямоугольников:

2. Составная формула правых прямоугольников:

3. Составная формула средних прямоугольников

Если отрезок 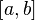разбивается узлами интегрирования и на каждом из элементарных отрезков применяется формула трапеций, то суммирование даст составную формулу трапеций

Для более точного вычисления интеграла, интервал разбивают на отрезков одинаковой длины и применяют формулу Симпсона на каждом из них. Значение исходного интеграла является суммой результатов интегрирования на всех отрезках.

где 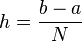— величина шага, а — узлы интегрирования, границы элементарных отрезков, на которых применяется формула Симпсона. Обычно для равномерной сетки данную формулу записывают в других обозначениях (отрезок разбит на 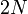узлов) в виде

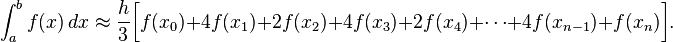
Также формулу можно записать используя только известные значения функции, то есть значения в узлах:

где означает что индекс меняется от единицы с шагом, равным двум. Следует обратить внимание на удвоение коэффициента перед суммой. Это связано с тем, что в данном случае роль промежуточных узлов играют исходные узлы интегрирования.

Общая погрешность 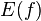при интегрировании по отрезку с шагом 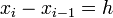(при этом, в частности, , ) определяется по формуле^[2]:

.

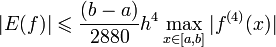При невозможности оценить погрешность с помощью максимума четвёртой производной (например, на заданном отрезке она не существует, либо стремится к бесконечности), можно использовать более грубую оценку:

.

Задания для контрольной работы

Во всех заданиях номер варианта соответствует последней цифре зачетной книжки

1. Найти решение нелинейного уравнения следующими методами: методом бисекции, методом хорд, методом Ньютона с точностью 0,01. При применении методов вычисления аналитически определить отрезок, на котором находится искомый корень.

№ варианта	Уравнения

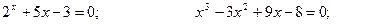
2. Определить экстремум функции при помощи методов золотого сечения и Ньютона

№ варианта	Уравнения

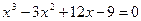
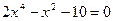
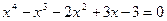
3.Найти решение системы линейных уравнений методом Гаусса-Зейделя

№	Система уравнений	№	Система уравнений

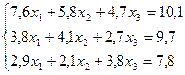
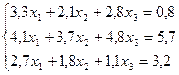
1. Решить дифференциальное уравнение методами Эйлера и Рунге-Кутта..

№	Уравнение	№	Уравнение

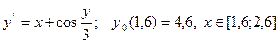
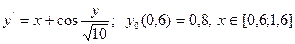
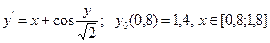
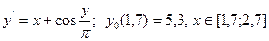
1. Вычислить определенный интеграл при помощи методов прямоугольников, трапеций и Симпсона согласно своего варианта, приняв n=10.

№	Интегралы	№	Интегралы

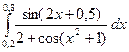
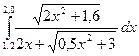
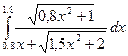
Дата добавления: 2017-01-14