Метод Гаусса-Зейделя

Метод Ньютона

Если строго унимодальная на отрезке функция f (x) дважды непрерывно дифференцируема на этом отрезке, то точку минимума этой функции можно найти путем решения уравнения 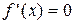методом Ньютона, иногда называемым методом касательных. Выбираем - начальное приближение. называемое обычно начальной точкой. Линеаризуем функцию в окрестности начальной точки, приближенно заменив дугу графика этой функции касательной в точке .

Рис. 6

Уравнений касательной имеет вид . Выберем в качестве следующего приближения к х * точку пересечения касательной с осью абсцисс (рис. 6). Получаем первый элемент итерационной последовательности На (k +1)-м шаге по найденной на предыдущем шаге точке можно найти точку

(5)

В общем случае сходимость метода Ньютона существенно зависит от выбора начальной точки Для надежной работы этого метода необходимо, чтобы вторая производная в некоторой окрестности искомой точки х * сохраняла знак, а начальная точка выбиралась из такой окрестности. В противном случае второе слагаемое в правой части (5) может стать неограниченным. Поскольку для дважды непрерывно дифференцируемой функции в точке минимума , то должно быть и . Поэтому говорят, что метод Ньютона обладает локальной сходимостью в том смысле, что надо выбрать хорошее начальное приближение, попадающее в такую окрестность точки х *, где . Однако проверка выполнения этого условия не всегда возможна. Достаточным условием монотонной сходи мости метода Ньютона будут постоянство в интервале между точками и х * знака производной f '"(x) и совпадение его со знаком . Оказывается, что в этом случае метод Ньютона обладает квадратичной скоростью сходимости в некоторой окрестности точки х *, причем

Решение систем линейных уравнений

Требуется найти решение системы m линейных уравнений, которая записывается в общем виде как

Расчетные формулы имеют вид:

т.е. для подсчета i –й компоненты (k +1)–го приближения к искомому вектору используется уже вычисленное на этом, т.е. (k +1)–м шаге, новые значения первых i –1 компонент.

Подробные формулы имеют вид:

Достаточное условие сходимости этого метода:

Начальное приближение:

Решение обыкновенных дифференциальных уравнений

Дата добавления: 2017-01-14