Поступальній та обертальний рухи твердого тіла. Додавання рухів твердого тіла

Тверде тіло як система матеріальних точок. Центр мас.

ПЛАН

1 Тверде тіло як система матеріальних точок. Центр мас.

2 Поступальній та обертальний рухи твердого тіла. Додавання рухів твердого тіла.

3 Вільні осі обертання. Гігроскопічний ефект і його застосування.

ЗМІСТ ТЕОРЕТИЧНОГО МАТЕРІАЛУ

Центром мас, або центром інерції системи матеріальних точок називається точка C, радіус-вектор 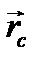якої дорівнює

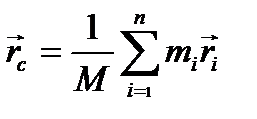, де - загальна маса всієї системи, – радіус-вектор i-ї матеріальної точки. Якщо радіус-вектори 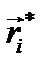проведені із центра мас C, то .

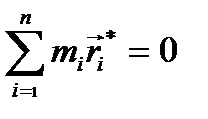Отже, центр мас - це геометрична точка, для якої сума добутків мас всіх матеріальних точок, що утворюють механічну систему, на їх радіус-вектори, які проведені з цієї точки, дорівнює нулю.

Швидкість центра мас

.

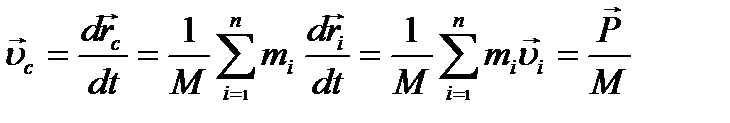Отже, , тобто імпульс системи дорівнює добутку величини маси системи на величину швидкості руху її центра мас. Продиференціювавши це рівняння за часом, отримуємо:

.

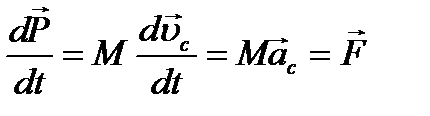Центр мас механічної системи рухається як матеріальна точка, в якій зосереджено всю масу системи і на яку діє сила, що дорівнює головному вектору прикладених до системи зовнішніх сил.

Абсолютно твердим тілом називається матеріальне тіло, геометрична форма якого і розміри не змінюються ні при яких механічних діях з боку інших тіл, а відстань між будь-якими двома його точками залишається постійною.

Кінематика твердого тіла,також як і динаміка твердого тіла,є одним з найбільш складних розділів курсу теоретичної механіки.

Задачі кінематики твердого тіла розпадаються на дві частини:

1. завдання руху і визначення кінематичних характеристик руху тіла в цілому;

2. визначення кінематичних характеристик (траєкторія, швидкість і прискорення) руху окремих точок тіла.

Існує п'ять видів руху твердого тіла:

1. поступальний рух;

2. обертання навколо нерухомої осі;

3. плаский рух;

4. обертання навколо нерухомої точки;

5. вільний рух.

Перші два називаються простими рухами твердого тіла:

Числом ступенів свободи твердого тіла називається число незалежних параметрів, які однозначно визначають положення тіла в просторі відносно даної системи відліку.

Рух твердого тіла багато в чому залежить від числа його ступенів свободи.

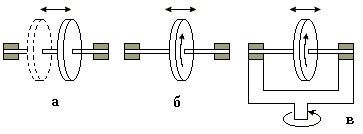
Рис. 1

Розглянемо приклад. Якщо диск, не обертаючись, може ковзати уздовж нерухомої в даній системі відліку осі (рис.1а),то в даній системі відліку він, очевидно, володіє лише одним ступенем свободи – положення диска однозначно визначається,скажімо, координатою x його центра, відлічуваною вздовж осі. Але якщо диск, крім того, може ще і обертатися (рис.1б), то він набуває ще одного ступеня свободи – до координати x додається кут повороту φ диска навколо осі. Якщо вісь з диском затиснута в рамці, яка може повертатися довкола вертикальної осі (рис.1 в), то число ступенів свободи дорівнює трьом – до x і φ додається кут повороту рамки φ.

Вільна матеріальна точка в просторі має три ступені свободи: наприклад декартові координати x, y і z. Координати точки можуть визначатись також в циліндричній (r, φ, z) і сферичній (r, φ, ῳ) системах відліку, але число параметрів, що однозначно визначають положення точки в просторі завжди три.

Матеріальна точка на площині має два ступені свободи. Якщо в площині вибрати систему координат x Оy, то координати x і y визначають положення точки на площині, а координата z тотожно дорівнює нулю.

Вільна матеріальна точка на поверхні будь-якого вигляду має два ступені свободи. Наприклад: положення точки на поверхні Землі визначається двома параметрами: широтою і довготою.

Рис. 2

Матеріальна точка на кривій будь-якого вигляду має один ступінь свободи. Параметром, що визначає положення точки на кривій, може бути, наприклад, відстань уздовж кривої від початку відліку.

Розглянемо дві матеріальні точки в просторі, сполучені жорстким стрижнем довжини l. Положення кожної точки визначається трьома параметрами, але на них накладена в'язь

Рівняння є рівнянням в'язі. З цього рівняння будь-яка одна координата може бути виражена через останні п'ять координат (п'ять незалежних параметрів). Тому ці дві точки мають () п'ять ступенів свободи.

Розглянемо три матеріальні точки в просторі, такі, що не лежать на одній прямій, сполучені трьома жорсткими стрижнями. Число ступенів свободи цих точок дорівнює () шести.

Вільне тверде тіло в загальному випадку має 6 ступенів свободи. Дійсно, положення тіла в просторі відносно якої-небудь системи відліку визначається завданням трьох його точок, таких, що не лежать на одній прямій, і відстані між точками в твердому тілі залишаються незмінними при будь-яких його рухах. Згідно з вище- сказаним, число ступенів свободи має дорівнює шести.

Дата добавления: 2017-01-14