Алгоритм жорданових перетворень

Лекція №3. Метод Жордана-Гаусса. Одержання невід’ємних розв’язків системи лінійних рівнянь і нерівностей.

Наведемо приклад.

Приклад 3.1. Нехай задана деяка система рівнянь:

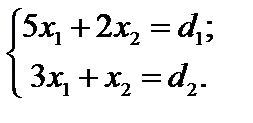
Розв’язавши її, маємо вирази:

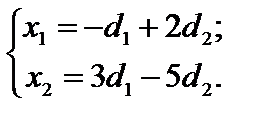
Зобразимо обидві системи у вигляді табл. 3.1 і 3.2:

Таблиця 3.1		Таблиця 3.2
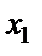
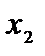
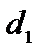
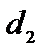
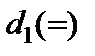
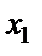				(=)	–1
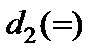
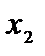				(=)		–5

У цих таблицях кожен рядок зображає рівняння (знаки „=” надалі опускаємо). Елементи рядка множаться на величини, що стоять зверху стовпчика, і ці добутки складаються.

Як видно з таблиць, розв’язування системи рівнянь зводиться до заміни величин, що стоять у рядках, на величини, що стоять зверху стовпчиків.

Досягти кожної такої заміни можна, застосовуючи так звані жорданові перетворення.

Розглянемо більш загальний випадок.

Приклад 3.2. Нехай задана система

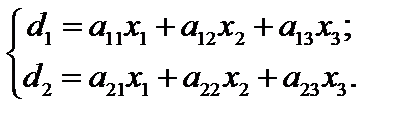
Зобразимо систему у вигляді табл. 3.3.

Таблиця 3.3

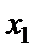
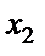
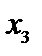
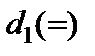
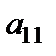
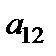
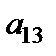
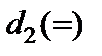
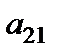
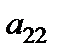
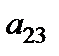
Визначимо з другого рівняння 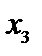і підставимо його значення у перше рівняння:

;

.

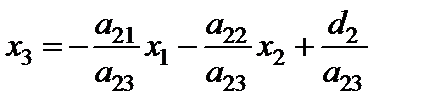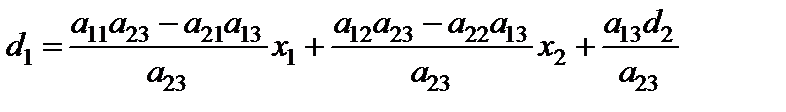Наведемо нові співвідношення у вигляді табл. 3.4.

Таблиця 3.4

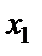
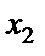
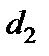
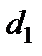
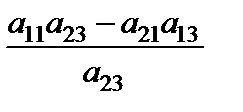
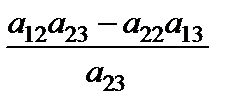
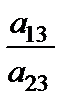
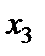
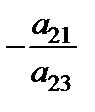
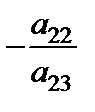
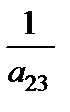
Здійснено так званий один крок жорданових перетворень, який полягає у заміні величини 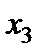на 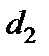і навпаки.

Опишемо алгоритм одного кроку жорданових перетворень, тобто у нашому прикладі переходу від табл. 3.3 до табл. 3.4.

1. Вибираємо пару величин – одну в рядку, другу в стовпчику, які будуть мінятися місцями. Відповідні рядок і стовпчик назвемо ведучими, а елемент на їх перетині – ведучим елементом. У табл. 3.3 це елемент 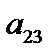. Позначимо ведучий елемент кружечком. Він не повинен дорівнювати 0.

2. Міняємо місцями вибрані величини.

3. На місце ведучого елемента ставимо одиницю.

4. Усім іншим елементам ведучого рядка змінюємо знаки.

5. Усі інші елементи ведучого стовпчика залишаємо без змін.

6. Усі інші елементи таблиці перетворюємо за правилом прямокутника, а саме:

- подумки утворюємо прямокутник, в якому шуканий і ведучий елементи стоять на кінцях діагоналі, яку назвемо головною;

- нове значення елементу дорівнює різниці добутків пар елементів, що стоять на головній та іншій діагоналях.

7. Усі без винятку елементи ділимо на ведучий елемент.

Деякі властивості жорданових перетворень:

- якщо ведучий елемент додатний, усі інші елементи ведучого рядка змінюють знаки;

- якщо ведучий елемент від’ємний, усі інші елементи ведучого стовпчика змінюють знаки.

3.2. Розв’язування систем лінійних рівнянь методом нуль-таблиць і жорданових перетворень

Приклад 3.3. Візьмемо систему рівнянь:

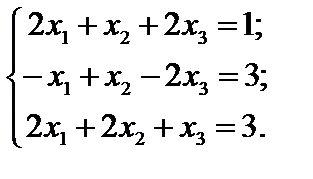
Перепишемо вільні члени у ліву частину; нулі для зручності запишемо зліва і зобразимо систему у вигляді табл. 3.5, яка називається нуль-таблицею:

Таблиця 3.5

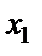
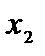
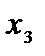
				–1
	–1		–2	–3
				–3

Послідовно застосовуючи жорданові перетворення, замінюємо нулі на величини 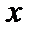. Ведучі елементи обводимо кружками.

Перехід від табл. 3.5 до наступної розберемо докладно. Нехай потрібно замінити нуль першого рядка на 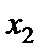. Ведучий елемент дорівнює одиниці. Будуємо табл. 3.6.

Таблиця 3.6

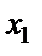
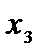
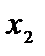
	–2		–2
	–3		–4	–2
	–2		–3	–1

Елементи першого рядка, крім ведучого, змінили знаки, у ведучому стовпчику – не змінилися. Решту елементів перераховуємо: на перетині другого рядка і стовпчика 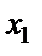нове значення елемента: 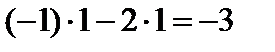; на перетині третього рядка і стовпчика 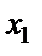: 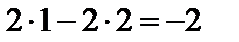тощо. Ділити на ведучий елемент не потрібно, оскільки він дорівнює одиниці.

При всіх перетвореннях рядки зберігають значення рівнянь.

Помічаємо, що стовпчик, в якому зверху стоїть нуль, не несе ніякої інформації. Тому його з таблиці викреслюємо. Подальші перетворення таблиць такі:

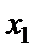
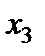
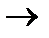
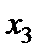
										(викреслюємо стовпчик з нулем і всі елементи ділимо на (-2))
	–2	–2			–2	–2	–4
	–3	–4	–2		–3	–1
	–2	–3	–1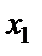

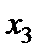
								(викрес- люємо стовпчик з нулем і ділимо на 1/2)
					3/2
	1/2	–1/2		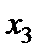	1/2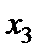
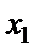
	-3/2	–1/2		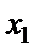-3/2	–1		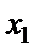-2

Пам’ятаючи, що кожен рядок таблиці є рівняння, маємо: .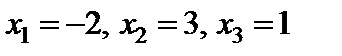

За допомогою цього методу можна також знаходити всі розв’язки недовизначеної системи 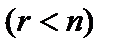, перевизначеної 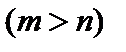, а також фіксувати відсутність розв’язків.

Дата добавления: 2015-07-13