Лекція 4. Сиплекс-метод розв’язування задачі лінійного програмування. Обгрунтування методу. Алгоритм одержання допустимого та оптимального планів

Розв’язування систем лінійних нерівностей

Приклад 3.7. Нехай задано систему нерівностей:

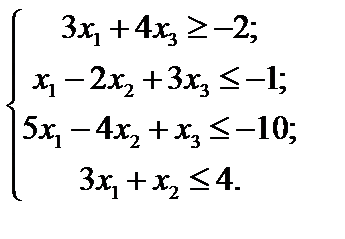
(3.1)

Введемо невід’ємні допоміжні змінні , 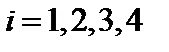для перетворення системи (4.1) у систему рівнянь:

(3.2)

Як відмічалося у п. 2.3, ці допоміжні змінні мають економічний зміст. Наприклад, якщо четверта нерівність системи (4.1) задає обмеження за ресурсом, то 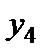є величина невикористаного ресурсу.

Визначимо величини 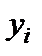з системи (4.2). Маємо:

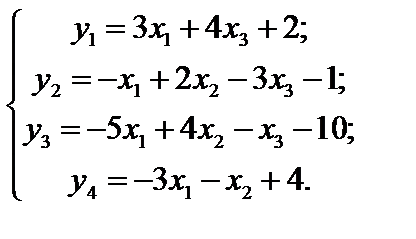
(3.3)

Систему (4.3) можна одержати простіше, а саме: перенесенням вільних членів у ліву частину, трансформацією нерівностей до знаку „ ” і прирівнянням лівої частини до .

Твердження. Розв’язати систему нерівностей (4.1) можна, знайшовши невід’ємні розв’язки системи рівнянь (4.3). Справді, вимога відповідає виконанню -ї нерівності з системи (4.1).

Симплекс-метод запроваджений американським математиком Дж. Данцігом (1947 р.). Розроблено велику кількість модифікацій цього методу. Розглянемо модифікацію з одним з найпростіших і ясних алгоритмів.

Розв`язання задачі розіб`ємо на етапи:

1. Запис ЗЛП з обмеженнями, в яких відношення суть «=» або «», і мінімізацією цільової функції. Тому, якщо у початковій постановці максимізується функція , у новій постановці мінімізується функція 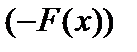. Задача, складена у такій формі, називається стандартною.

2. Складання симплекс-таблиці.

3. Знаходження допустимого розв`язку і базисного допустимого розв`язку. Допустимимрозв`язком є розв`язок, що задовольняє систему (2.4) і умови (2.6). Базисним розв`язком називається допустимий розв`язок з вільними змінними, що дорівнюють нулю.

4. Знаходження оптимального розв`язку. Оптимальним є базисний розв`язок, що мінімізує цільову функцію (2.5).

Розглянемо застосування симплекс-методу на прикладі 2.2 з підмодуля 2.

Аналітичний розв’язок будемо співставляти з графічним.

4.1. Складання симплекс-таблиці

Повернемося до прикладу 2.2 з підмодуля 2.

Запишемо систему обмежень (2.12) у стандартному вигляді, як показано в п. 5.1. Маємо систему (2.13).

Цільову функцію 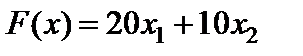треба максимізувати, а за стандартом функція мінімізується. Тому умову 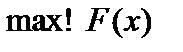заміняємо умовою .

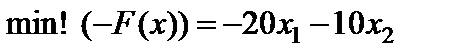Складаємо так звану симплекс-таблицю 5.1, де кожній нерівності системи (2.13) відповідає рядок таблиці; (як і раніше, знаки ”=” після 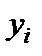опускаємо). Для цільової функції відводиться нижній рядок.

На цій основі складемо симплекс-таблицю (табл. 4.1).

Таблиця 4.1

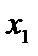
			-5
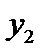
		-1
	-1	-3
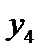
			-2
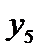
	-1
-F	-20	-10

У табл. 4.1 кожному рядку відповідає одне обмеження системи. Після першого стовпчика неявно розуміється знак рівності, а коефіцієнти в рядку множаться на величини, що стоять над стовпчиком. Коефіцієнти рядка називаються оцінками. Змінні , що стоять у лівому стовпчику, утворюють початковий базис, а змінні і 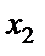, що стоять над стовпчиками, є вільними. Згідно з постановкою загальної ЗЛП усі змінні повинні бути невід`ємними: .

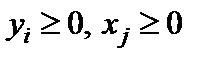Вільні змінні, як було пояснено вище, повинні дорівнювати нулю, щоб ми весь час знаходилися в якійсь вершині допустимої області. Якщо 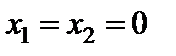, то значення базисних змінних 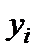дорівнюють вільним членам таблиці. На рис. 2.2 з лекції 2 стан табл. 4.1 відповідає точці 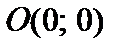. Ми ще не знаходимося у допустимій області, про що свідчить наявність від`ємних значень 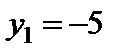і .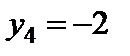

Щоб знайти допустимий, а потім оптимальний розв`язок, треба змінити склад базисних і вільних змінних та їх значення. Це досягається застосуванням жорданових перетворень.

Дата добавления: 2015-07-13