Знаходження допустимого розв’язку

Допустимим і одночасно базисним планом буде такий, де вільні члени невід’ємні, а вільні змінні дорівнюють нулю. Для досягнення допустимого плану робимо послідовні перетворення, керуючись правилом 1 (підмодуль 4).

Примітки. 1. Елементи рядка 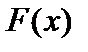обчислюються за загальними правилами жорданових перетворень.

2. Початкове значення функції 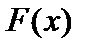чи записується в останній клітині рядка (у нашому випадку, коли 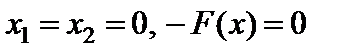). Надалі у цій клітині автоматично з’являються наступні значення цільової функції.

3. Із рядка ведучі елементи не вибираються.

Робимо послідовні перетворення табл. 4.1. Із відношень від’ємних вільних членів до додатних елементів у їх рядках: 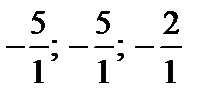вибираємо згідно з правилом 1 найменше; ведучий елемент обводимо кружком.

Після перетворення табл. 4.1 буде мати вигляд табл. 4.2

Таблиця 4.2

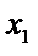
		-1
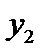
		-2
	-1	-2
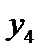
			-2
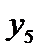
	-1		-2
-F	-20		-100

З табл. 4.2 видно, що ми знаходимося у точці: 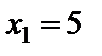, , тобто в точці К. Автоматично прораховується значення цільової функції: , тобто . Оскільки ще залишилися від’ємні вільні члени, ми ще не знаходимося в допустимій області, як це видно з рис. 2.2 лекції 2.

У табл. 4.2 є вибір між відношеннями 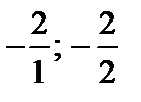; вибираємо за правилом 1 перше з них і формуємо нову табл. 4.3.

Таблиця 4.3

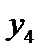
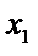
		-1
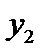
		-2
	-1	-2
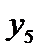
	-1
-F	-20		-80

Отже, знаходимося у точці 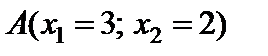. Це точка, яка вже належить допустимій області, про що свідчать невід`ємні значення вільних членів.

Точки області можна визначити й інакше, беручи перетин ліній, що відповідають , тобто ліній 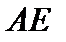і .

Примітка. Як випливає з властивостей жорданових перетворень, змінити знак вільного члена можна тільки з допомогою додатного ведучого елементу.

Якщо у рядку з від’ємним вільним членом немає додатних елементів, змінити знак вільного члена неможливо. Це свідчить про відсутність допустимого розв’язку (система обмежень суперечлива).

Дата добавления: 2015-07-13