Знаходження невід’ємних розв’язків системи рівнянь

Як вже зазначалося, ЗЛП потребує невід’ємних розв’язків (див. умову (2.6)). Якщо у системі обмежень 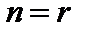, розв’язок єдиний і серед є від’ємні, фіксуємо неможливість знайти невід’ємні розв’язки. Якщо ж крім базисних змінних є вільні, серед множини розв’язків можуть знайтися невід’ємні.

Приклад 2.6. Розглянемо систему:

Складемо табл. 4.1. Ранг матриці системи не більше трьох, тому принаймні дві змінні виявляться вільними.

Таблиця 4.1

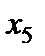
		–1				–2
		–1			–1	–1
	–1					–3

Зробимо три кроки жорданових перетворень.

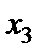
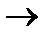
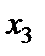
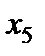
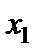
–1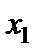

–1

–2

–1

–3

–5

–8

Таблиця 4.2

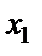
			–1
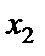
			–3
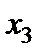
	–6	–1

Пояснимо останню таблицю. Як зазначалося у п. 2.5, вільні змінні повинні дорівнювати нулю, щоб ми знаходилися весь час у вершинах многогранника. Отже, базисні змінні вважаємо рівними вільним членам. У табл. 4.2 маємо такий розв’язок: ; .

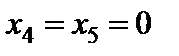Невід’ємні розв’язки – це такі розв’язки, коли невід’ємними є вільні члени, бо вільні змінні дорівнюють нулю. Згідно з властивостями жорданових перетворень (п. 3.1) змінити знак у рядку (в т.ч. знак вільного члена) можна за допомогою додатного ведучого елементу. У табл. 4.2 є чотири таких елементи: у першому рядку „1” і „1”, у другому „2” і „1”. Якому віддати перевагу, щоб, змінивши знак у одному рядку, не одержати від’ємне значення вільного члена у другому рядку? Для систематичного прямування до невід’ємного розв’язку слід застосовувати правило 1.

Правило 1. Для пошуку невід’ємних розв’язків системи треба знайти відношення від’ємних вільних членів до додатних елементів у їх рядках, і з цих відношень взяти найменше. Елемент, який дає таке відношення, беремо за ведучий.

Здійснимо це на табл. 4.2.

З відношень: найменшим є останнє. Тому робимо перетворення і складаємо таблицю 4.3.

Таблиця 4.3

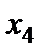
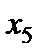
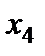
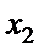
			–1		–1
			–3		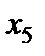–2
	–6	–1			–4	–1

Табл. 4.3 дає один з варіантів невід’ємних розв’язків: .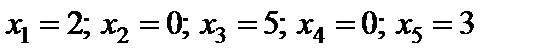

Примітки: 1. Для одержання невід’ємних розв’язків може бути потрібно виконати 2, 3... кроки перетворень з додержанням правила 1.

2. Якщо у рядку з від’ємним вільним членом немає додатних елементів, змінити знак вільного члена неможливо. Це є ознакою відсутності невід’ємних розв’язків.

Обґрунтування правила 1. Нехай у 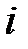-му рядку є від’ємний вільний член 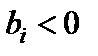і додатний елемент .

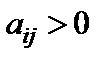У рядку 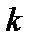є від’ємний вільний член 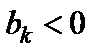і додатний елемент (див. фрагмент таблиці, який наведений нижче).

.

Нехай справджується нерівність , з якої слідує: .

Тоді, згідно з правилом 1, треба взяти ведучим елемент 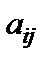. Знак вільного члена у рядку зміниться на додатний.

Знайдемо нове значення вільного члена :

.

Враховуючи попередню нерівність, бачимо, що , тобто змінився знак вільного члена і в рядку .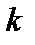

Примітка. Економічне обґрунтування правила 1 полягає в тому, що спочатку усувається найбільший дефіцит ресурсу.

Дата добавления: 2015-07-13