Знаходження оптимального розв’язку

Розглянемо табл. 4.3 детальніше. Останній рядок таблиці дає розв’язок:

.

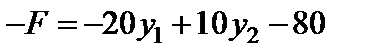Змінн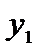і і є вільними і дорівнюють нулю, тому . Припустимо, що в базис ввели змінну . Вона стане додатною. Тоді величина збільшиться, тобто цільова функція погіршиться (нагадаємо, що за прийнятим нами стандартом функція мінімізується).

У разі, якщо всі оцінки додатні, зміна складу і значень базисних і вільних змінних призвела б тільки до погіршення цільової функції.

Отже, ознакою оптимальності плану є невід’ємність оцінок.

Прямуючи до оптимального плану, потрібно зробити оцінки додатними.

Із властивостей жорданових перетворень (п. 3.1) ясно, що змінити знак у стовпчику можна з допомогою від’ємного ведучого елемента. Але при цьому треба не вийти за межі допустимої області. Це досягається застосуванням правила 2.

Правило 2. Для прямування до оптимального плану беремо всі відношення додатних вільних членів до від’ємних елементів у їх рядках, які належать стовпчикам з від’ємними оцінками, і з цих відношень беремо найбільше. Елемент, що дає таке відношення, беремо за ведучий.

Обґрунтування правила 2. Нехай у стовпчику з від’ємною оцінкою є два від’ємних елементи: 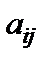і , вільні члени у цих рядках і 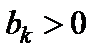відповідно.

Якщо має місце співвідношення 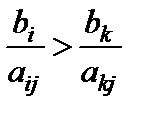, то, помноживши обидві частини нерівності на додатне число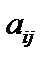 , одержимо: 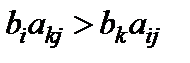. Тоді за правилом 2 ведучим елементом вибираємо (див. фрагмент матриці).

Знак залишиться після перетворення додатним. Нове ж значення дорівнює:

;

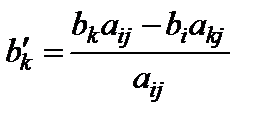чисельник і знаменник одержаного виразу від’ємні, тому , і ми не виходимо за межі допустимої області.

Повертаємося до табл. 4.3.

Згідно з правилом 2 у табл. 4.3 беремо відношення 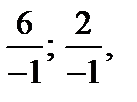більше з них , тому ведучим елементом беремо “-1” в рядку . Зробимо перетворення з урахуванням ділення всіх елементів “-1”, тобто зміни знаків всіх елементів:

Таблиця 4.4

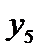
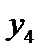
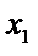
	-1
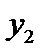
	-1
		-4
	-1
-F		-30	-120

Знаходимося у точці , яка ще не є оптимальною, оскільки існує від’ємна оцінка „–30”. Знову застосуємо правило 2. Ведучий елемент “–4”. Зробимо перетворення і одержимо табл. 4.5.

Таблиця 4.5

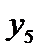
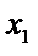
	-3/4	-1/4
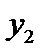
	-1
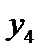
	1/4	-1/4
	1/4	-1/4
	-1/2	-1/2
-F	25/2	15/2	-150

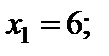
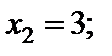
Ми знаходимося в точці . Оскільки всі оцінки додатні, план оптимальний. У цьому плані . Значення , тому оптимальне значення цільової функції .

Примітки. 1. Якщо в процесі пошуку допустимого плану виявиться, що у рядку, де вільний член від`ємний, немає додатних елементів, то задача не має допустимого плану. Економічне значення цього факту: система обмежень суперечлива, наприклад, для виконання заданого обсягу робіт не вистачає ресурсів.

2. Якщо в процесі пошуку оптимального плану у стовпчику з від`ємною оцінкою не знайдеться від`ємних елементів, то задача не має оптимального плану, тобто цільова функція не обмежена.

3. Якщо деякі обмеження є рівностями, то у відповідному рядку стовпчика базисних змінних стоїть нуль. Його треба замінити будь-якою вільною змінною.

Розглянемо приклад 5.1, де складена початкова симплекс-табл. 4.6. Поміняємо місцями нуль у другому рядку і змінну 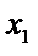. Маємо таблицю 4.7

У табл. 4.7 стовпчик з верхнім нулем не несе ніякої інформації, і його з табл. 4.7 викреслюємо та отримуємо табл. 4.8:

Таблиця 4.6

	-2
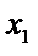
		-2
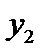
	-1		-6
-F	-15	-10

Таблиця 4.7

	-2	-3
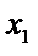
			-5
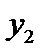
	-1		-1
-F	-15	-40

Таблиця 4.8

	-3
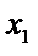
		-5
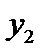
		-1
-F	-40

Подальші дії з табл. 5.8. виконуємо за описаними вище правилами.

Дата добавления: 2015-07-13