Обратная матрица

Формула вычисления элементов обратной матрицы: .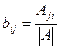

Алгоритм нахождения .

1. Проверить невырожденность с помощью определителя.

2. Составить матрицу из дополняющих миноров M_ij.

3. Изменить знаки в шахматном порядке, то есть домножить на (-1)^i+j, где i,j - номера строки и столбца.

4. Транспонировать полученную матрицу.

5. Поделить на определитель исходной матрицы.

Задача 3. Найти обратную матрицу .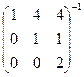

Решение. Сначала ищем определитель. Так как матрица треугольная, то достаточно перемножить числа по диагонали. .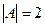

Строим матрицу, состоящую из дополняющих миноров.

Зачёркиваем ту строку и тот столбец, где находится элемент, и остаётся минор 2 порядка из 4 элементов.

На схеме показано, что именно надо зачеркнуть:

= = .

Теперь надо сменить знаки в шахматном порядке, т.е. переходим от миноров к алгебраическим дополнениям. Обведено красным, где надо менять знак. Ясно, что 0 остаётся 0, там знак менять нет смысла.

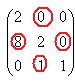
Получили: = .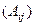

Транспонируем эту матрицу, то есть бывшие строки запишем по столбцам.

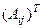= . И осталось разделить на .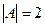

Ответ. .

Задача 4. Найти ранг матрицы .

Решение. Поменяем 1-ю и 2-ю строки, так чтобы в верхнем левом углу было число 1. Это удобнее для преобразований к треугольной форме методом Гаусса. Ранг при этом не меняется. После этого, вычтем 1-ю строку с коэффициентом 1 либо 4 из последующих, так, чтобы обнулить всё ниде углового элемента.

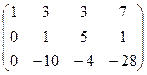
Ещё мы поменяли 2 и 3 строку, чтобы продолжить метод Гаусса без излишних дробных коэффициентов.

Теперь 2-ю строку, домноженную на 10, прибавим к 3-й.

.

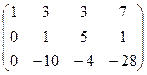
Итак, исходная матрица сводится к такой, в которой уже есть треугольная сруктура в первых трёх столбцах.

Очевидно, что обведённый минор равен 46, не равен 0. Он 3-го порядка, поэтому ранг равен 3.

Ответ: .

Дата добавления: 2017-01-14