
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Контрольная работа № 2
|
|
|
|
Решение.
Контрольная работа № 1.
Семестр
1. Подведение под знак дифференциала, преобразования.
2. Интегрирование по частям.
3. Интегрирование рациональных дробей.
4. Интегрирование иррациональностей и тригонометрических функций.
Варианты для самостоятельного решения:
Вариант 1. Найти неопределённые интегралы:
1.  2.
2.  3.
3.  4.
4. 
Вариант 2. Найти неопределённые интегралы:
1.  2).
2). 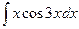 3.
3.  4.
4. 
Аналогичные задачи из практических занятий:
Задача 1.1. Вычислить  .
.
Решение.  =
=  =
=  =
=
=  =
=  =
= 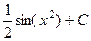 .
.
Ответ. 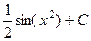 .
.
Задача 1.2. Вычислить  .
.
Решение. Дискриминант знаменателя отрицательный, поэтому здесь невозможно сделать как в прошлой задаче, так как нет корней знаменателя и дробь невозможно свести к виду 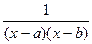 .
.
Но при D < 0 можно выделить полный квадрат:
 =
=  =
= 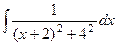 .
.
С помощью замены  сводится к интегралу:
сводится к интегралу:
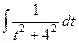 =
= 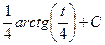 , и далее с помощью обратной замены получаем ответ:
, и далее с помощью обратной замены получаем ответ:  .
.
Ответ.  .
.
Задача 2.1. Вычислить  .
.
Решение. Пусть  , так надо, чтобы понизилась степень на следующем шаге. Составим таблицу:
, так надо, чтобы понизилась степень на следующем шаге. Составим таблицу:

| 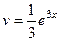
|

| 
|
Тогда  =
=  =
=  .
.
Ответ.  .
.
Задача 2.2. Вычислить 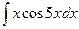 .
.

| 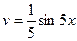
|

| 
|
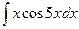 =
=  =
=  .
.
Ответ.  .
.
Задача 3. Вычислить интеграл  .
.
Решение. Как видим, здесь корень 1 имеет кратность 2. Разложение на простейшие дроби нельзя проводить так, как будто бы здесь три независимых множителя 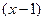 ,
, 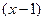 ,
,  , т.е.
, т.е.  , иначе получится противоречие, ведь общий знаменатель будет содержать всего лишь 1-ю степень
, иначе получится противоречие, ведь общий знаменатель будет содержать всего лишь 1-ю степень 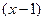 но никак не вторую. Надо степени знаменателя учитывать по возрастающей, до кратности корня, а именно, так:
но никак не вторую. Надо степени знаменателя учитывать по возрастающей, до кратности корня, а именно, так:  .
.
Приведём к общему знаменателю:
 .
.
Числитель этой дроби равен числителю исходной, той, которая была в интеграле:
 .
.
 , система:
, система:
 . Построим расширенную матрицу и решим систему уравнений:
. Построим расширенную матрицу и решим систему уравнений:


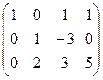

 .
.
Система приведена к виду: 
Тогда 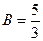 ,
,  ,
,  . И теперь интеграл распадается на сумму трёх интегралов:
. И теперь интеграл распадается на сумму трёх интегралов:  .
.
В 1 и 3 слагаемых - как раньше, а вот во 2-м логарифм в ответе не получится, ведь тут уже 2-я а не 1-я степень в знаменателе.
Полезно вспомнить, что 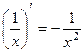 .
.
То есть, интеграл от -2 степени будет содержать -1 степень, и меняется знак.
Ответ.  .
.
Задача 4.1. Вычислить интеграл  .
.
Решение. Здесь есть корни порядка 2 и 3. Наименьшее общее кратное, НОК(2,3) = 6. Поэтому замена  . При этом,
. При этом,
 ,
,  ,
,  ,
,
 ,
,
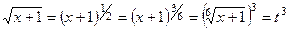 .
.
Тогда  =
=  =
=  =
=
 =
=  .
.
Сделаем обратную замену и получим ответ:
Ответ.  .
.
Задача 4.2. Вычислить интеграл  .
.
Решение. Здесь тоже суммарная степень чётная, замена  .
.
 .
.  ,
,  .
.
 =
=  =
=  =
=
 =
= 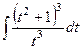 =
= 
здесь мы воспользовались формулой 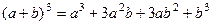 .
.
 =
=  .
.
После обратной замены получаем ответ:
Ответ.  .
.
1. Определённый интеграл и его приложения.
2. Несобственный интеграл.
3. Двойной интеграл.
4. Дифф. уравнения 1 порядка с разделяющимися переменными.
Варианты для самостоятельного решения:
Вариант 1.
1.Вычислить площадь области, ограниченной кривыми:
 ,
,  ,
,  .
.
2. Найти несобственный интеграл  .
.
3. Найти двойной интеграл  , где
, где 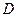 - треугольник с вершинами (0,0), (1,1), (1,3).
- треугольник с вершинами (0,0), (1,1), (1,3).
4. Решить дифф. уравнение  .
.
Вариант 2.
1.Вычислить площадь области, ограниченной кривыми:
 ,
,  ,
,  .
.
2. Найти несобственный интеграл  .
.
3. Вычислить в полярных координатах интеграл от функции  по 1-й четверти круга радиуса 1.
по 1-й четверти круга радиуса 1.
4. Дифф. уравнение 1 порядка  .
.
Аналогичные задачи из практических занятий:
Задача 1.1. Вычислить 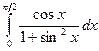
Решение. 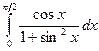 =
= 
здесь мы можем заменить  на
на  , но тогда нужно сделать пересчёт верхнего и нижнего пределов. Если
, но тогда нужно сделать пересчёт верхнего и нижнего пределов. Если  то
то  , т.е.
, т.е.  .
.
 =
=  =
=  =
= 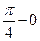 =
= 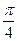 .
.
А можно было сначала вычислять интеграл как неопределённый, тогда надо было бы вернуться к исходной переменной  (то есть сделать обратную замену), но пределы можно не пересчитывать.
(то есть сделать обратную замену), но пределы можно не пересчитывать.
 =
=  =
=  =
= 
 =
=  =
=  =
= 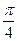 .
.
Ответ. 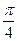 .
.
Задача 1.2. Найти площадь области, ограниченной линиями 
|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 142; Нарушение авторских прав?; Мы поможем в написании вашей работы!