
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Контрольная работа № 3
|
|
|
|
Решение.
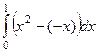 =
=  =
=  =
=  =
=  .
.

Ответ.  .
.
Задача 2. Найти несобственный интеграл 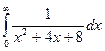 .
.
Решение. 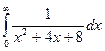 =
=  =
= 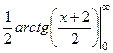 =
=
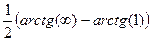 =
=  =
= 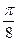 .
.
Здесь под символом 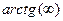 понимается предел
понимается предел  .
.
Ответ. 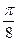 .
.
Задача 3.1. Вычислить интеграл  по треугольнику D, вершины которого: (0,0),(1,0),(0,1).
по треугольнику D, вершины которого: (0,0),(1,0),(0,1).
Решение. Строение треугольника понятно (см. чертёж).
Наклонная линия задаётся уравнением  .
.

Вычисление:  =
=  =
=
 =
= 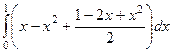 =
= 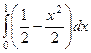 =
=
 =
=  . Ответ.
. Ответ. 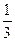 .
.
Задача 3.2. Вычислить  , где D - четверть круга радиуса 1 (в первой координатной четверти).
, где D - четверть круга радиуса 1 (в первой координатной четверти).
Решение. Заменим  ,
,  , а также умножим на якобиан
, а также умножим на якобиан  .
.

 =
=  =
=
 =
= 
Дальше остаётся интеграл от одной переменной, там можно применять обычный способ, подведение под знак дифференциала.
 =
=  =
=  =
=  =
=  =
=  .
.
Ответ.  .
.
Задача 4. Решить уравнение  .
.
Решение. 
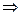

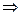

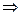

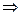
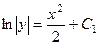
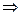

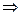
 .
.
Ответ.  .
.
Проверка. Если  , то
, то  , действительно, производная имеет лишний множитель
, действительно, производная имеет лишний множитель  по сравнению с исходной функцией, и подходит в качестве решения уравнения
по сравнению с исходной функцией, и подходит в качестве решения уравнения  .
.
1. Линейные дифф. уравнения 2 порядка с задачей Коши.
2. Действия с комплексными числами.
3. Формула Муавра.
4. Числовые ряды.
Вариант для самостоятельного решения:
1. Решить линейное однородное уравнение  , найти частное решение при
, найти частное решение при  ,
,  .
.
2. Поделить  .
.
3. Вычислить в показательной форме: 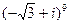
ответ дать в виде a+bi.
4. Исследовать сходимость ряда 
Аналогичные задачи из практических занятий:
Задача 1. Найти частное решение дифф. уравнения  при условиях Коши:
при условиях Коши:  .
.
Решение. Характеристическое уравнение:  , его корни:
, его корни:  ,
,  . Тогда ФСР состоит из
. Тогда ФСР состоит из  и
и 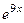 , общее решение такое:
, общее решение такое: 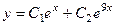 .
.
Теперь найдём решение задачи Коши. Сначала запишем функцию и её производную:
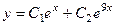 и
и  .
.
Кроме того, у нас есть информация:  .
.
Тогда  ,
,  . Получается система уравнений
. Получается система уравнений
 вычитая 1-е уравнение из 2-го, находим,
вычитая 1-е уравнение из 2-го, находим,  , т.е.
, т.е. 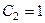 , тогда
, тогда  . Тогда частное решение:
. Тогда частное решение:  .
.
Ответ.  .
.
Задача 2. Разделить  двумя способами:
двумя способами:
1) с помощью умножения на сопряжённое число.
2) в показательной форме.
Решение. 1)  =
=  =
=  .
.
2)  =
=  =
= 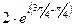 =
=  =
=  =
= 
Ответ.  .
.
Задача 3. Возвести в степень в алгебраической и показательной форме:  .
.
Решение. Перейдём к показательной форме, для этого сначала найдём модуль и аргумент числа  с помощью чертежа. Число в 1-й четверти, угол 45 градусов.
с помощью чертежа. Число в 1-й четверти, угол 45 градусов.
 =
=  . По формуле Муавра,
. По формуле Муавра,  =
=
 =
=  =
=  =
=  =
=  =
=  .
.
Чертёж, показывающий, расположение  на плоскости, это число выделено красным цветом:
на плоскости, это число выделено красным цветом:

Задача 4. 
Решение. Запишем предел отношения модуля (n+1) члена ряда к модулю n-го. При этом мы отбрасываем знакочередование.
 =
= 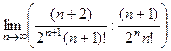 =
=  =
=
 =
=  .
.
Итак,  , ряд сходится (абсолютно).
, ряд сходится (абсолютно).
|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 133; Нарушение авторских прав?; Мы поможем в написании вашей работы!