Погрешности результатов численного решения задач

Следует правильно воспринимать тот факт, что вычисления, проводимые при помощи ЭВМ, являются приближенными. Не вызывает недоумения, что в реальной жизни нам приходится иметь дело с приближенными величинами. Так любые экспериментальные измерения проводятся с некоторой погрешностью, часто не имеет смысла оперировать слишком малыми долями оцениваемых величин, нахождение точных значений искомой величины приводит к неоправданным затратам времени, сил и средств. Однако непременным требованием к вычислениям является получение решения с контролируемой погрешностью.

Анализируя вычисления и обработку данных при помощи ЭВМ можно выделить следующие причины погрешности результата:

1. физическая и математическая модели являются лишь приближенными описаниями реального процесса или явления;

2. исходные данные, используемые для расчетов, содержат погрешности, так как их получают из экспериментов или предварительных вычислений;

3. применяемые для расчетов численные методы, как правило, являются приближенными;

4. представление чисел в ЭВМ и выполнение арифметических операций проводятся приближенно.

Пусть 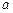– некоторое точное, а 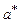– приближенное решение. Его погрешность будет складываться из неустранимой погрешности 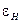, обусловленной первыми двумя причинами, погрешности численного метода 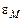и погрешности представления и оперирования данными ЭВМ 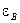. Обычно исходят из предположения, что физическая и математическая модели фиксированы, и начальные данные для расчетов задаются извне, т.е. величина 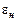задана и не меняется в процессе вычислений. Зная величину неустранимой погрешности, можно выбрать соответствующий ей численный метод. Желательно, чтобы погрешность метода была в 2-10 раз меньше неустранимой. Большое значение 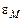существенно снижает точность расчетных данных, слишком малое ее значение неоправданно увеличивает временя вычисления. Величина погрешности представления и оперирования данными ЭВМ 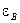зависит от типа ЭВМ и, как правило, должна быть хотя бы на порядок меньше погрешности метода .

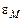Для оценки точности вычислений используют два вида погрешностей – абсолютную и относительную. Абсолютной погрешностью приближенного решения 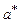называют модуль разности между точным и приближенным значениями:

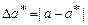(1.1)

Как видно, из величины абсолютной погрешности невозможно определить качество приближения. Например, пусть абсолютная погрешность вычисления составляет 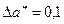. Много это или мало? Очевидно, что для 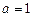– это большая величина, в то время как для 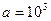– это приемлемая точность. Для определения качества приближения вводят относительную погрешность (при 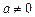) в виде:

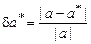.(1.2)

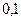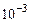Для приведенного ранее примера составляет и . Использование относительной погрешности удобно и потому, что не зависит от масштабов и единиц измерения.

Анализ погрешностей на численные вычисления описан во многих специализированных трудах и справочниках. Ограничимся только некоторыми правилами обработки приближенных данных. Наиболее важные из них определяются следующими утверждениями (здесь введены обозначения: ; ):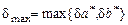

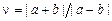относительные погрешности суммы и разности определяются максимальной погрешностью величин:

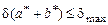,(1.3)

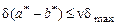.(1.4)

1. относительные погрешности произведения и частного определяются следующими величинами:

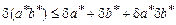,(1.5)

.
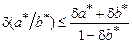(1.6)

2. относительная погрешность вычисления дифференцируемой в некоторой области функции имеет вид:

.

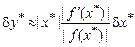(1.7)

Неравенство (1.3) означает, что при суммировании приближенных чисел одного знака потери точности не происходит, а при вычитании приближенных чисел одного знака ошибка возрастает в 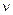раз и возможна существенная потеря точности. Например, если числа 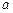и близки настолько, что 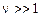, т.е. , не исключена полная или почти полная потеря точности. Таким образом, при построении численного метода следует избегать вычитания близких чисел. Если такое вычитание неизбежно, то необходимо учитывать потерю точности примерно в 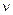раз. При малых относительных погрешностях чисел 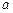и правило 2 используют в следующем виде: 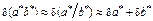. Всякий раз, когда на ЭВМ производится расчет по формуле, вносится некоторая неустранимая ошибка, вызванная тем, что вместо 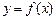вычисляется .

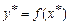Анализируя погрешности, следует сказать и о неточностях вычислений на ЭВМ, вносимых машинной арифметикой. Следует отметить две их причины. Первая – ЭВМ работает в двоичном (или кратном двоичному) коде. Например, число 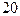в двоичном коде будет иметь вид 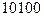. Вторая – конечное количество разрядов, используемых для записи чисел. Первая особенность приводит к тому, что такое «простое» число как, например, 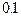, в двоичном коде будет иметь вид периодической дроби 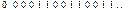. Вторая особенность проявляется в том, что при умножении значительного количества чисел больших единицы, происходит переполнение разрядов (машинная бесконечность), а меньших единицы – исчезновение порядка (машинный нуль).

Дата добавления: 2017-01-14