Численное дифференцирование

Численное дифференцирование и интегрирование

В прикладных задачах в результате расчетов или измерений получаются таблицы значений, определяющие некоторые функциональные зависимости. Как правило, такие таблицы для получения необходимых для исследователей новых характеристик требуется обрабатывать. Очень часто приходится находить производные или интегралы от соответствующих этим зависимостям функций. Численное дифференцирование и интегрирование применяется в тех случаях, когда производную или интеграл от функции трудно или невозможно вычислить аналитически, а также в случае, когда сама функция задана таблицей. Кроме этого формулы численного дифференцирования используются при разработке вычислительных методов решения дифференциальных и нелинейных уравнений, поиска точек экстремума и т.д. Необходимо отметить, что формулы численного интегрирования в целом хорошо обусловлены, т.е. погрешность задания функции оказывает контролируемое влияние на точность вычисления.

Простейшие формулы численного дифференцирования основаны на определении производной функции (рассматривается случай функции, зависящей от одной переменной)

. (5.1)

Заменяя предельный переход конечной разностью, получаем простейшие приближенные формулы вычисления первой производной

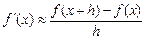(5.2)

и

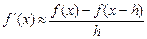.(5.3)

Здесь принимают фиксированные значения и 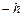, соответственно, где 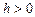представляет собой некоторый малый параметр. Приближенную производную, определяемую формулой (5.2), называют правой разностной производной, а определяемую (5.3) – левой.

Геометрическая интерпретация приведенных соотношений достаточно проста. Если существует некоторая функция , то производная этой функции 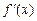представляет собой тангенс угла наклона касательной в точке 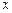. Приближенное равенство (5.2) заменяет касательную на секущую графика функции, проходящую через точк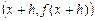и и 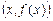, а равенство (5.3) – на секущую, проходящую через 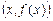и 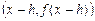. Так же из геометрических соображений ясно, что можно провести секущую графика функции и через точк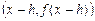и и 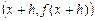. В этом случае получаем, так называемую, центральную разностную формулу вычисления производной

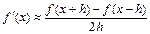. (5.4)

Вопрос о том, какую из формул (5.2), (5.3) или (5.4) выбрать для вычислений, определяется требуемой точностью вычисления производной.

Для получения формул численного дифференцирования высших порядков используются интерполяционные многочлены или метод неопределенных коэффициентов. Наиболее универсальным является метод неопределенных коэффициентов. Аппроксимируем исследуемую функцию многочленом -ой степени

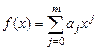.(5.5)

В методе неопределенных коэффициентов принимается, что -я производная функции в точке 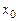может быть приближенно выражена через значения самой функции в известных точках ,...,

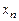
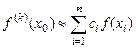. (5.6)

Значения коэффициентов 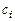выбираются таким образом, чтобы формула (5.6) была точна для многочленов максимально высокой степени. Подставляя выражение (5.5) в (5.6), получаем тождество (при )

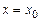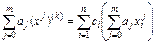.(5.7)

Учтем, что

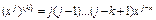,(5.8)

тогда для того, чтобы равенство (5.8) выполнялось необходимо и достаточно равенство коэффициентов при 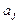в правой и левой частях равенства. Исходя из этого условия, получаем линейную систему уравнений

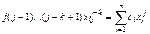(5.9)

относительно неизвестных 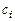при 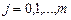. Если 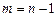, то число уравнений равно числу неизвестных, а определитель системы является определителем Вронского, поэтому отличен от нуля. Следовательно, всегда можно построить формулу численного дифференцирования по 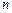точкам, точную для многочленов 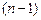-ой степени.

Для проверки выражения (5.9) построим формулу численного дифференцирования по трем точкам

(5.10)

точную для многочленов второй степени (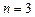 следовательно 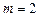). Система уравнений (5.9) будет иметь вид ()

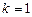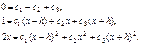(5.11)

Решая эту систему, получаем 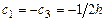, 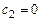. Следовательно, формула (5.21) будет иметь вид

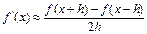, (5.12)

что полностью совпадает с формулой (5.4)

Построим формулу вычисления второй производной, используя те же узлы

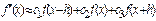. (5.13)

Из условий точности формулы для , 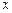и 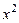получаем систему уравнений

(5.14)

Откуда получаем 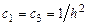, 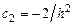. Следовательно

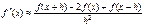, (5.15)

В качестве примера рассмотрим вычисление производной функции 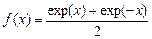на отрезке [-5,5]. Функция 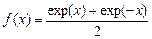вычисляется на заданном отрезке с шагом 0,1, затем, используя правую разностную производную, вычисляется ее производная по точкам и сравнивается на графике с аналитическим значением .

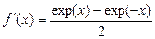Дата добавления: 2017-01-14