Решение пере- и недоопределенных СЛАУ

Метод наименьших квадратов

Будем рассматривать систему линейных алгебраических уравнений вида

. (6.1)

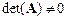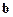Из курса линейной алгебры известно, что в том случае, когда и число уравнений равно числу неизвестных система имеет единственное решение. На практике часто встречаются задачи, в которых либо число уравнений не совпадает с числом неизвестных, либо матрица или вектор заданы не полностью или не точно. Решение таких задач строится методом наименьших квадратов (МНК).

Задача наименьших квадратов в разных дисциплинах называется по-разному. Например, математически это есть задача отыскания для заданной точки функционального пространства ближайшей точки в заданном подпространстве. Статистика вводит в свою постановку задачи вероятностные распределения и оперирует терминами типа регрессионный анализ. Инженерный подход к решению проблемы анализа сложных систем приводит к задачам оценивания параметров или фильтрации.

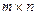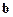Главное состоит в том, что все эти задачи содержат в себе одну и ту же центральную проблему, а именно последовательность линейных задач наименьших квадратов. Эту проблему можно сформулировать следующим образом. Пусть дана действительная -матрица ранга и действительный -вектор . Задача наименьших квадратов состоит в нахождении действительного 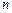-вектора , минимизирующий евклидову длину (норму) вектора невязки .

Здесь не выдвигается никаких предположений относительно сравнительной величины параметров и 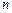, поэтому удобно все многообразие разделить на шесть случаев (рис.6.1).

В основе решения задач такого типа лежит представление 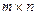-матрицы в виде произведения , где и 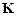– ортогональные матрицы. Напомним, что матрица называется ортогональной, если ( – единичная матрица), из единственности обратной матрицы следует, что и 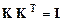. Любое разложение 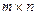-матрицы такого типа называется его ортогональным разложением. Важным свойством ортогональных матриц является сохранение евклидовой длины при умножении. Это значит, что для любого -вектора и любой ортогональной -матрицы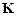

.(6.2)

В контексте решения задачи наименьших квадратов минимизации евклидовой нормы имеем

(6.3)

для произвольной ортогональной -матрицы 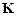и 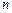-вектора .

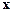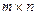Использование такого разложение позволяет сформулировать задачу метода наименьших квадратов в следующем виде. Пусть – ортогональная -матрица ранга , представленная в виде

,(6.4)

где и 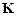– ортогональные матрицы размерности соответственно и , а – 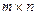-матрица вида

,(6.5)

где 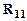– -матрица ранга .

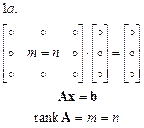
Рисунок 6.1. Шесть случаев задачи МНК в соответствии со сравнительной характеристикой величин , 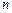и ранга .

Определим вектор

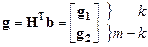(6.6)

и новую переменную

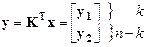(6.7)

Определим как единственное решение системы .

Тогда:

1. Все решения задачи о минимизации имеют вид

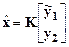, где

– произвольно. (6.8)

2. Любой такой вектор приводит к одному и тому же вектору невязки

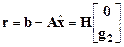.(6.9)

3. Для нормы вектора невязки справедливо

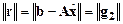
(6.10)

4. Единственным решением минимальной длины является вектор

.(6.11)

Заменим согласно формуле (4) и получим

. (6.12)

из уравнений (6.6)-(6.11) следует, что

(6.13)

для всех . Очевидно, что правая часть (6.13) имеет минимальное значение , если

.(6.14)

Это уравнение допускает единственное решение , так как ранг 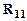равен . Общее решение выражается формулой

,(6.15)

где произвольно. Для вектора из (6.11) имеем

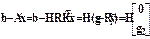, (6.16)

что устанавливает равенство (6.9). Среди векторов вида (6.15) наименьшую длину (норму) будет иметь тот, для которого 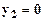, поэтому из (6.8) получим

,(6.17)

что доказывает (6.11).

В случае 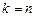или величины с размерностями и отсутствуют. В частности, при 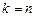решение задачи наименьших квадратов единственно. Отметим, что решение минимальной длины (нормы), множество всех решений и минимальное значение для нормы вектора невязки определяются единственным образом и не зависят от вида конкретного ортогонального разложения.

Для дальнейшего ограничимся несколькими утверждениями, приведенными без доказательств.

1. Если – 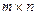-матрица, то существует ортогональная -матрица 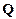такая, что в матрице 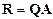под главной диагональю стоят только нулевые компоненты. Такое представление матрицы называется 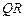-разложением.

2. Если – 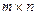-матрица ранга , то существует ортогональная -матрица 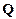и -матрица перестановок такие, что

,(6.18)

где – верхняя треугольная -матрица ранга . При этом для -подматрицы 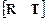существует ортогональная матрица такая, что

,

(6.19)

где – нижняя треугольная матрица ранга .

Первое утверждение дает возможность построить разложение матрицы в случаях и , где . Действительно, ( – единичная -матрица). Для случая (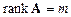) запишем или ( – единичная -матрица). Второе утверждение дает возможность построить разложения для случаев - При этом матрица представима в виде

,(6.20)

где 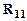– невырожденная треугольная -матрица.

Дата добавления: 2017-01-14