
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методы решения задачи Коши
|
|
|
|
Решение обыкновенных дифференциальных уравнений
Обыкновенными дифференциальными уравнениями (ОДУ) описывается множество физических явлений: задачи движения системы взаимодействующих материальных точек, химической кинетики, электрических цепей, сопротивления материалов и многие другие. Некоторые важные задачи также сводятся к уравнениям в частных производных. Таким образом, решение ОДУ занимает важное место среди прикладных задач физики, химии и техники.
Конкретная прикладная задача может приводить к дифференциальному уравнению любого порядка, однако ОДУ  -го порядка
-го порядка

(7.1)
можно привести к эквивалентной системе  дифференциальных уравнений первого порядка путем введения новых переменных
дифференциальных уравнений первого порядка путем введения новых переменных  :
: 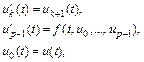 (7.2)
(7.2)
где  . Поэтому очень важно уметь решать ОДУ первого порядка.
. Поэтому очень важно уметь решать ОДУ первого порядка.
Различают три основных типа задач для обыкновенных дифференциальных уравнений: задачи Коши (задача с начальными условиями), краевые задачи и задачи на собственные значения. Ограничимся рассмотрением методов только первых двух задач. При этом будем предполагать, что решение существует, единственно и обладает необходимым свойством гладкости, т.е. искомая функция столько раз может быть продифференцирована, сколько это необходимо.
Для решения задачи Коши рассмотрим ОДУ первого порядка, тогда формулировка задачи выглядит следующим образом: требуется найти непрерывную при  функцию
функцию  , удовлетворяющую дифференциальному уравнению
, удовлетворяющую дифференциальному уравнению
 (7.3)
(7.3)
и начальному условию
 ,(7.4)
,(7.4)
где  – известная функция двух аргументов. Если функция
– известная функция двух аргументов. Если функция  определена в прямоугольнике
определена в прямоугольнике  удовлетворяет в области
удовлетворяет в области 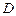 по переменной
по переменной  условию Липшица:
условию Липшица:
 (7.5)
(7.5)
для всех  и
и  , то задача (7.3) имеет единственное решение.
, то задача (7.3) имеет единственное решение.
Для решения задачи Коши введем по переменному  равномерную сетку с шагом
равномерную сетку с шагом  , т.е. рассмотрим множество точек
, т.е. рассмотрим множество точек  . Будем обозначать через
. Будем обозначать через 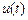 точное решение, а через
точное решение, а через  – приближенное. Отметим, что приближенное решение является сеточной функцией, т.е. определено только в точках сетки
– приближенное. Отметим, что приближенное решение является сеточной функцией, т.е. определено только в точках сетки  .
.
Рассмотрим простейшие численные методы, получаемые из наглядных соображений. Пусть известно значение 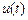 и требуется вычислить значение
и требуется вычислить значение  . Рассмотрим равенство
. Рассмотрим равенство
 . (7.6)
. (7.6)
Считая промежуток  достаточно малым, заменим интеграл в правой части по формуле левых прямоугольников на
достаточно малым, заменим интеграл в правой части по формуле левых прямоугольников на 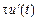 , при этом погрешность будет иметь порядок
, при этом погрешность будет иметь порядок  . Получим
. Получим
 ,(7.7)
,(7.7)
т.к. 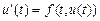 , то
, то
 . (7.8)
. (7.8)
Принимая, что  и
и 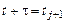 , получаем явную формулу Эйлера для решения задачи Коши
, получаем явную формулу Эйлера для решения задачи Коши
 .
.
(7.9)
Аналогично, используя формулу правых прямоугольником для аппроксимации интеграла в (7.6), получим неявную формулу Эйлера
 (7.10)
(7.10)
Для получения более точной расчетной формулы необходимо более точно аппроксимировать интеграл в правой части (7.6). Воспользуемся формулой трапеций с погрешностью 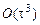
 , (7.11)
, (7.11)
что с учетом (7.3) приводит к соотношению
(7.12)
Полученная расчетная формула называется неявной формулой Адамса второго порядка точности
(7.13)
В некоторых случаях, когда  линейна по
линейна по  , уравнение (7.13) может быть разрешено относительно
, уравнение (7.13) может быть разрешено относительно  . Обычно же это уравнение неразрешимо явно, поэтому используют следующий алгоритм нахождения решения, использующий метод простой итерации,
. Обычно же это уравнение неразрешимо явно, поэтому используют следующий алгоритм нахождения решения, использующий метод простой итерации,
 .
.
Здесь  – номер итерации, а начальное приближение можно определить по явной формуле Эйлера
– номер итерации, а начальное приближение можно определить по явной формуле Эйлера
 .
.
Фактически необходимо сделать одну или две итерации для достижения заданной точности.
|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 187; Нарушение авторских прав?; Мы поможем в написании вашей работы!