
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Погрешности методов численного дифференцирования
|
|
|
|
Оценим погрешности методов вычисления. Для разностных правой и левой производных будут справедливы следующие выражения
 (5.16)
(5.16)
и
 , (5.17)
, (5.17)
а для центральной
 . (5.18)
. (5.18)
Для оценки погрешностей левых и правых разностных производных первую производную можно получить из разложения в ряд Тейлора в виде
 . (5.19)
. (5.19)
Здесь и ниже 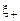 и
и  – некоторые точки, расположенные на интервалах
– некоторые точки, расположенные на интервалах  и
и 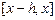 соответственно. Откуда погрешности этих методов будут иметь вид
соответственно. Откуда погрешности этих методов будут иметь вид
 , (5.20)
, (5.20)
а оценка абсолютных погрешностей будет удовлетворять неравенству  , (5.21)
, (5.21)
где  . (5.22)
. (5.22)
Таким образом, формулы (5.2) и (5.3) вычисления правой и левой разностных производных имеют первый порядок точности по  .
.
Для центральной разностной производной соответствующие разложения функций  в ряд Тейлора должны учитывать и производную третьего порядка (вторая производная при вычитании исчезает)
в ряд Тейлора должны учитывать и производную третьего порядка (вторая производная при вычитании исчезает)
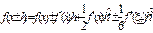 . (5.23)
. (5.23)
Отсюда получим
 (5.24)
(5.24)
и для оценки абсолютной погрешности будет справедливо неравенство
 (5.25)
(5.25)
где

(5.26)
Таким образом, производная 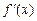 вычисляется при помощи формул центральной разностной производной со вторым порядком точности по
вычисляется при помощи формул центральной разностной производной со вторым порядком точности по  , т.е. точнее, чем по формулам (5.2) и (5.3).
, т.е. точнее, чем по формулам (5.2) и (5.3).
Очень часто уменьшение погрешности метода, в данном случае метода численного дифференцирования, сопровождается ростом влияния погрешности исходных данных и вычислительной погрешности. Численное дифференцирование относится именно к таким задачам, которые обычно называют плохо обусловленными.
Оценим совместное влияния погрешностей вычисления и метода для вычисления первой производной. Пусть значение производной вычисляется по формуле (5.3), тогда погрешность метода можно оценить по соотношению (5.21). Если значения функции 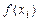 известны с некоторой погрешностью
известны с некоторой погрешностью  (
( ), то погрешность вычисления
), то погрешность вычисления 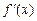 будет содержать дополнительное слагаемое
будет содержать дополнительное слагаемое
 ,(5.27)
,(5.27)
Пренебрегая для простоты погрешностью округления, имеем оценку погрешности в следующем виде

.(5.28)
Из формулы (5.28) очевидно, что уменьшение  не приводит к увеличению точности вычисления производной, так как возрастает ошибка, связанная с погрешностью определения функции (рисунок 5.1). Погрешности
не приводит к увеличению точности вычисления производной, так как возрастает ошибка, связанная с погрешностью определения функции (рисунок 5.1). Погрешности 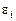 возникают вследствие ошибок измерения или предыдущего вычисления по приближенным формулам. Из соотношения (5.28) можно найти оптимальное значение разбиения, находя экстремум правой части, такое
возникают вследствие ошибок измерения или предыдущего вычисления по приближенным формулам. Из соотношения (5.28) можно найти оптимальное значение разбиения, находя экстремум правой части, такое  будет равно
будет равно
 .(5.29)
.(5.29)
Отметим, что повышение точности метода лишь отчасти повышает точность вычисления производной.

Рисунок 5.1. Зависимость погрешности вычисления первой производной от величины шага.
5.3. Численное интегрирование. Простейшие методы К численному интегрированию прибегают в тех случаях, когда невозможно аналитически получить первообразную, или когда такая первообразная имеет неудобный или слишком сложный для вычисления вид. Основной задачей численного интегрирования является вычисление интеграла вида
 ,(5.29)
,(5.29)
где 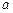 и
и  – нижний и верхний пределы интегрирования, а функция
– нижний и верхний пределы интегрирования, а функция  – непрерывная на отрезке
– непрерывная на отрезке 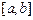 .
.
Сущность большинства методов вычисления определенных интегралов состоит в замене подынтегральной функции  аппроксимирующей функцией
аппроксимирующей функцией 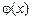 , для которой можно легко записать первообразную в элементарных функциях, т.е.
, для которой можно легко записать первообразную в элементарных функциях, т.е.
 ,(5.30)
,(5.30)
где  – погрешность вычисления.
– погрешность вычисления.
Используемые на практике методы численного интегрирования можно условно сгруппировать в зависимости от способа аппроксимации подынтегральной функции.
1. Методы полиномиальной аппроксимации  , которые отличаются друг от друга степенью используемого полинома, что определяет количество узлов, где необходимо вычислить подынтегральную функцию. Это достаточно простые для реализации методы. В частности к этим методам относятся простейшие формулы – прямоугольников, трапеций, Симпсона, которые обобщаются формулами Ньютона-Котеса.
, которые отличаются друг от друга степенью используемого полинома, что определяет количество узлов, где необходимо вычислить подынтегральную функцию. Это достаточно простые для реализации методы. В частности к этим методам относятся простейшие формулы – прямоугольников, трапеций, Симпсона, которые обобщаются формулами Ньютона-Котеса.
2. Сплайновые методы базируются на аппроксимации  сплайнами. Методы этого класса отличаются по типу выбранных сплайнов и используются в основном там, где применяются алгоритмы сплайновой аппроксимации для обработки данных.
сплайнами. Методы этого класса отличаются по типу выбранных сплайнов и используются в основном там, где применяются алгоритмы сплайновой аппроксимации для обработки данных.
3. Методы наивысшей алгебраической точности, использующие неравноотстоящие узлы, расположенные по алгоритму, обеспечивающую минимальную погрешность интегрирования, используются для наиболее сложных функций при заданном количестве узлов вычисления функции  .
.
4. Методы, основанные на случайном выборе узлов, где определяются значения интегрируемой функции. Эти методы (методы Монте-Карло) используются для вычисления кратных интегралов, для которых они наиболее эффективны.
В дальнейшем ограничимся методами первой и второй группы, а также рассмотрим алгоритмы метода Монте-Карло для кратных интегралов.
Наиболее широко на практике для вычисления определенных интегралов используются квадратурные формулы – приближенные равенства вида
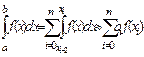 , (5.31)
, (5.31)
что соответствует разбиению полного интеграла на сумму интегралов от функции по элементарным отрезкам. Здесь 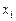 – некоторые точки (узлы) из отрезка
– некоторые точки (узлы) из отрезка  , разбитого на
, разбитого на  элементарных отрезков
элементарных отрезков 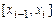 , при этом
, при этом  , а
, а 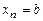 , а
, а 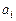 – некоторые коэффициенты. Сумма, стоящая в правой части выражения (5.31) называется квадратурной суммой. Погрешность вычисления по этой формуле определяется выражением
– некоторые коэффициенты. Сумма, стоящая в правой части выражения (5.31) называется квадратурной суммой. Погрешность вычисления по этой формуле определяется выражением
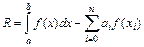 . (5.32)
. (5.32)
Заметим, что интеграл вида (5.29) определяет площадь фигуры ограниченной прямыми  ,
,  ,
,  и графиком функции
и графиком функции  . Для вычисления этой и площади и соответственно интеграла ее можно разбить на простые фигуры. На этом и основаны простейшие методы вычисления интеграла (5.29).
. Для вычисления этой и площади и соответственно интеграла ее можно разбить на простые фигуры. На этом и основаны простейшие методы вычисления интеграла (5.29).
Формулы прямоугольников. Рассмотрим разбиение отрезка 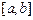 на
на 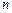 элементарных отрезков
элементарных отрезков  , пусть для простоты
, пусть для простоты  , тогда каждому значению
, тогда каждому значению 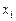 можно поставить в соответствие значение функции
можно поставить в соответствие значение функции 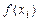 . Рассматривая
. Рассматривая 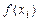 как высоту прямоугольника с основанием
как высоту прямоугольника с основанием  можно получить две формулы: формулу левых прямоугольников (рисунок 5.2)
можно получить две формулы: формулу левых прямоугольников (рисунок 5.2)
 (5.33)
(5.33)
и формулу правых прямоугольников
 .(5.34)
.(5.34)
Аналогичным образом за высоту прямоугольника можно взять его середину. В этом случае отрезок обычно разбивают на  отрезков и рассматривают только нечетные узлы, что эквивалентно рассмотрению прямоугольников высотой, равной значению функции в середине элементарного отрезка. Квадратурная формула называется формулой средних прямоугольников (рисунок 5.3) и имеет вид
отрезков и рассматривают только нечетные узлы, что эквивалентно рассмотрению прямоугольников высотой, равной значению функции в середине элементарного отрезка. Квадратурная формула называется формулой средних прямоугольников (рисунок 5.3) и имеет вид
 .(5.35)
.(5.35)

Рисунок 5.2. Интегрирование по формуле левых прямоугольников
Интересно отметить, что формулы левых и правых прямоугольников фактически заменяют интеграл верхними и нижними суммами Дарбу и, к сожалению, имеют высокую погрешность. Это в равной степени относится и к формуле средних прямоугольников.
Формула трапеций. Следующая простейшая формула получается, если рассматривать в качестве приближения не прямоугольник, а трапецию с высотами  и
и 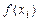 (рисунок 5.4). В этом случае площадь
(рисунок 5.4). В этом случае площадь  -ой элементарной трапеции с основанием
-ой элементарной трапеции с основанием  будет иметь вид
будет иметь вид
 . (5.36)
. (5.36)

Рисунок 5.3. Интегрирование по формуле средних прямоугольников
Приближенное значение интеграла в свою очередь будет определяться как
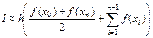 . (5.37)
. (5.37)
Эта формула соответствует приближенной замене площади исходной криволинейной трапеции площадью фигуры, ограниченной ломаной линией. 
Рисунок 5.4. Интегрирование по формуле трапеций
В качестве примера приведена программа вычисления интеграла от функции  на отрезке [-5,5] по формуле правых прямоугольников.
на отрезке [-5,5] по формуле правых прямоугольников.
|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 627; Нарушение авторских прав?; Мы поможем в написании вашей работы!