Кусочно-полиномиальная интерполяция

Разделенные разности и интерполяционная формула Ньютона

Для вычислений удобна форма записи интерполяционного полинома, связанная с разделенными разностями. Введем разделенные разности для известных точек :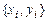

нулевого порядка ;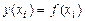

первого порядка ;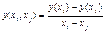

второго порядка 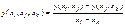и т.д.

Разделенные разности имеют размерности соответствующих производных функции 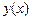. Если исходная функция представима в виде полинома 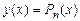степени 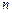, то разделенные разности можно записать относительно этого полинома соответственно:

первого порядка ;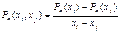

второго порядка 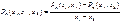и т.д.

Для разделенных разностей справедливо равенство

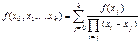
(4.12)

доказательство которого можно провести по индукции.

Непосредственно из (4.12) вытекает ряд следствий:

1) Разделенная разность является линейным оператором относительно функции :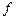

2) Разделенная разность есть симметрическая функция своих аргументов 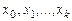(т.е. не изменяется при любой их перестановке).

Если функция задана в точках 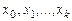, то

таблицу

называют таблицей ее разделенных разностей.

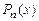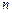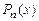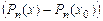Построим интерполяционные формулы, используя разделенные разности полиномов. Пусть – полином степени . Вычтя из константу , получим полином , который обращается в нуль при 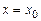и поэтому делится нацело на 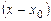. Следовательно, первая разделенная разность полинома 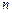степени

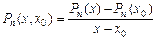(4.13)

есть полином 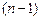степени относительно 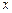и в силу симметричности выражения (4.13) относительно 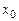. Аналогично вторая разность 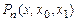есть полином 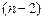степени. В самом деле, числитель разделенной разности

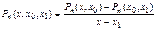(4.14)

обращается в нуль при 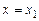и, значит, нацело делится на 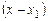, а степень полинома при этом уменьшается на единицу. Далее можно показать, что разделенная разность 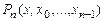есть полином нулевой степени, т.е. константа, а разделенные разности более высоких порядков равны нулю.

Выразив из (4.13) полином 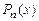, а из (4.14) полином 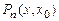получим

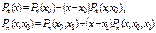(4.15)

и т.д. Эта цепочка соотношений конечна, так как 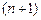разделенная разность полинома равна нулю. Последовательно подставив эти соотношения друг в друга, получим формулу

которая содержит значения разделенных разностей полинома в узлах 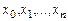. Однако значения интерполяционного полинома в узлах по определению совпадают со значениями функции 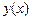и поэтому разделенные разности функци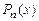й и 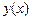равны. Подставив в полученную формулу разделенные разности функции 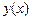, получим интерполяционный полином в виде

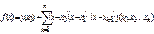. (4.16)

Этот полином называется интерполяционным полиномом Ньютона.

Пример. Пусть функция 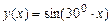. Выберем в качестве узлов точки 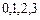. Составим таблицу разделенных разностей: (нетуJ)

С учетом найденных величин, получим

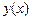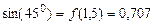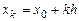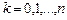Применив интерполяционный полином, можно приближенно найти значения функции в точках, не совпадающих с узлами. В нашем случае, например, . Если узлы интерполяции отстоят друг от друга на одном и том же расстоянии, т.е. удовлетворяют соотношению , где , а 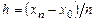, то, обозначив 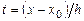, получим следующие равенства:

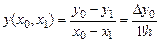
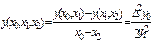и т.д. В общем случае

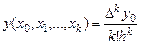, (4.17)

где 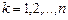. Тогда

Поэтому интерполяционный полином (4.16) преобразуется к виду

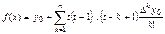.(4.18)

, Интерполяция многочленом Лагранжа или Ньютона на отрезке 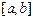с использованием большого числа узлов приводит к увеличению степени интерполяционного многочлена, что затрудняет вычисления и увеличивает погрешность. Для решения этой проблемы отрезок 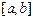разбивают на части и на каждой из них приближенно заменяют функцию 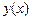многочленом некоторой, обычно не слишком большой степени. Такой подход к решению задачи интерполяции называется кусочно-полиномиальной интерполяцией. Одним из видов кусочно-полиномиальной интерполяции является интерполяцией с помощью сплайн-функций.

Сплайн-функцией или сплайном называют кусочно-полиномиальную функцию, определенную на отрезке 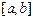и имеющую на нем некоторое число непрерывных производных. Слово «spline» означает гибкую линейку, используемую для проведения гладких кривых через заданные точки плоскости. Преимущество сплайнов перед обычной интерполяцией заключается в том, что их сходимость к функции 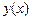осуществляется быстрее. Более того, использование сплайнов повышает устойчивость процесса вычислений. Рассмотрим распространенный в вычислительной практике случай, когда сплайн определяется с помощью многочленов степени .

Интерполяционным сплайном порядка 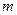, соответствующим данной функции 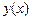и данным узлам 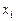, называется функция 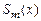, удовлетворяющая следующим условиям:

1) на каждом из отрезков 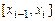она является многочленом степени ();

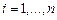2) на отрезке 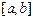она имеет непрерывные производные до порядка ;

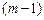3) 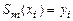, при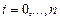

Если 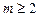, то для единственности 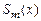следует задать дополнительно еще 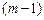условий, которые обычно задаются на концах отрезка 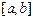либо произвольно, либо из дополнительной информации о поведени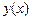и . При 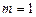получаем так называемый метод ломаных (каждая точка соединяется с соседними прямой линией). Очевидно, что 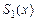равномерно сходится к непрерывной на отрезке 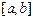функции 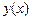. Равномерная сходимость имеет место для квадратичного 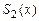и кубического сплайна 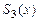, причем скорость сходимости повышается вместе с увеличением порядка сплайна и повышением гладкости функции .

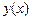Рассмотрим построение кубического сплайна 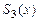. На каждом из отрезков 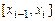, где 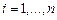, будем искать функцию 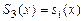в виде многочлена третьей степени

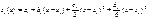.(4.19)

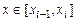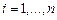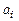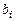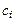Здесь , , а , , и 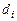– коэффициенты, подлежащие определению. Выясним смысл введенных коэффициентов, для чего вычислим первые три производные функции (4.19):

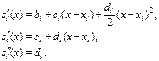Отсюда для 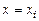получим

(4.20)

Сучетом условия 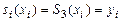получим, что для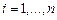

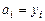.(4.21)

Доопределим, кроме этого, 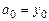. Таким образом, коэффициенты 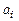определены.

Требование непрерывности функции 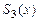приводит к условиям при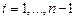 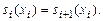(4.22)

Из выражения (4.22)с учетом выражений (4.18), получаем при 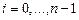уравнения

(4.23)

Обозначив 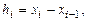перепишем в виде

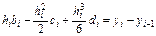, для 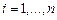. (4.24)

Условия непрерывности первой производной 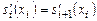для 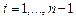, приведут к уравнениям

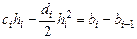, для 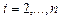, (4.25)

а из условий непрерывности второй производной получим

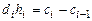, для 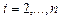.(4.26)

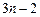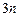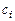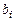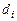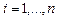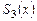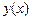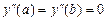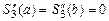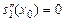Объединяя уравнения (4.24)-(4.26), получим систему уравнений относительно неизвестных , , (при ). Два недостающих условия получают, задавая те или иные граничные условия для . Пусть для выполняются условия , тогда или и 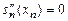, т.е. получаем два уравнения

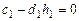и . (4.27)

Заметим, что условие 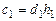совпадает с уравнением (4.26) при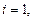 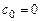. Таким образом, для определения неизвестных коэффициентов приходим к к замкнутой системе уравнений:

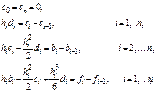(4.28)

Систему уравнений (4.28) можно решать различными методами, однако путем преобразований ее можно свести к решению СЛАУ с трехдиагональной матрицей:

(4.29)

а 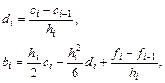(4.30)

где 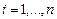. Отметим, что систему уравнений (4.29) можно решать с помощью метода прогонки.

Дата добавления: 2017-01-14