Метод простой итерации

Метод хорд

Алгоритм

Метод дихотомии (деления отрезка пополам)

Допустим, что каким-либо способом определен отрезок изоляции корня. Это означает, что график функции пересекает ось абсцисс (Рис.2.1), т.е. значения и 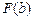имеют разные знаки. (Если график функции касается оси абсцисс, то необходимо решить уравнение, аналогичное (2.1), но только для производной функции. Этот случай рассматриваться не будет.) Для определенности будем считать, что , а .

Рис.2.1. Метод дихотомии

Найдем середину отрезка число 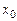(нулевое приближение)

.(2.2)

Значение будет либо меньше нуля, либо больше нуля (если , то корень найден). Очевидно, что решение будет лежать на отрезке 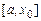. Далее найденный отрезок опять делим пополам и находим первое приближение

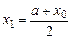(2.2)

и опять определяем знак . После 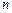приближений исходный отрезок, на котором ищется решение, будет уменьшен в раз. Например, после 10 итераций решение будет находиться в отрезке длиной , а после 20 – . Вычисления проводятся до тех пор, пока не выполнится условие: или .

1. Определяем знаки и .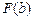

2. Вычисляем нулевое приближение – .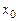

3. Определяем знак .

4. Если 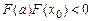, то определяем новый отрезок, где находится решение – 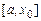, иначе .

5. Вычисляем первое приближение и т.д.

Рассмотрим для примера уравнение

.(2.3)

Это уравнение имеет два корня, локализованных на отрезках 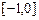и . Убедимся, что на концах этих отрезков функция принимает разные знаки

.(2.4)

Будем искать один из корней на отрезке 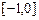, используя вариант программной реализации метода на языке MatLab с точностью не менее

Одним из вариантов, развивающих метод дихотомии, является определение приближенного решения методом хорд. Графически этот метод представлен на рисунке 2.2. Суть данного метода заключается в том, что приближенное решение определяется в точке пересечения прямой, соединяющей концы отрезка .

Рис.2.2. Метод хорд

Уравнение прямой, проходящей через концы отрезка, имеет вид

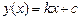,(2.5)

где

,(2.6)

а 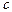можно выразить двумя способами, приводящими к одному и тому же значению:

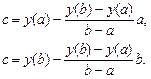(2.7)

Соответственно для нулевого приближения так же будем иметь два варианта (одинаковых по значению) 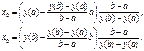(2.8)

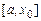Далее, как и в методе дихотомии, определяем знак и выбираем из отрезков и 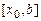тот, у которого знаки функции на концах различаются. Продолжая этот процесс, находим последовательно второе, третье и последующие приближения. Выход из процесса приближения и алгоритм метода хорд такой же, как и для метода дихотомии.

Если от уравнения (2.1) перейти к эквивалентному уравнению

,(2.9)

то возможно использование итерационной процедуры нахождения корня уравнения. При этом функцию часто называют итерационной.

Процедура нахождения корня достаточно проста: выберем какое-либо начальное приближение 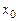и подставим его в уравнение (2.9). В результате получим первое приближение , которое опять подставим в уравнение. Продолжая этот процесс неограниченно, получим последовательность приближений к корню, вычисляемую по формуле

.(2.10)

Очевидно, что если существует предел последовательности и функция непрерывна, то получим равенство

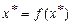,(2.11)

а это значит, что – корень уравнения (2.9). Отметим, что метод простой итерации является одношаговым.

Геометрическая интерпретация метода представлена на Рис.2.3. Из рисунка видно, что метод простой итерации может приводить как к сходящейся к решению процедуре, так и к расходящейся.

Для использования этого метода необходимо установить критерий его сходимости. Будем считать, что в итерационной формуле (2.10)

(2.12)

где и – отклонения 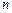-го и ()-го приближения от корня . Если процесс уточнения осуществляется вблизи корня , то функцию приближенно можно представить в виде первых двух членов разложения в ряд Тейлора. Используя выражение (2.11), получаем

.(2.13)

Принимая во внимание равенство (2.11), имеем

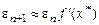.(2.14)

Для обеспечения сходимости итерационного процесса необходимо потребовать, чтобы , что приводит к условию , откуда 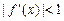. (2.15) Если , то имеет место односторонняя сходимость к решению (Рис.2.3,а); если же выполняется условие , то сходимость будет двухсторонней (Рис.2.3,б). В случае, когда 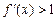или (Рис.2.3,в и 2.3,г), итерационный процесс расходится.

Зная условие сходимости итерационного процесса (2.15), можно разработать процедуру перехода от уравнения (2.1) к уравнению (2.9) так, чтобы итерационный процесс сходился наиболее эффективным образом. Для этого умножим обе части равенства (2.1) на некоторую константу и прибавим 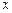, получим

.(2.16)

Таким образом, искомая функция будет иметь вид

.(2.17)

Произвольный параметр выбирается так, чтобы было обеспечено условие сходимости. Наиболее удобно выбрать этот параметр из условия для обеспечения двухсторонней сходимости, при этом критерий окончания итерационного процесса будет наиболее простым

.(2.18)

Наибольшая скорость сходимости будет, когда , то есть .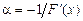

Дата добавления: 2017-01-14