Метод Ньютона-Котеса и его модификация

Простейшие формулы численного интегрирования были получены фактически в приближении постоянства или линейной зависимости функции на отрезке 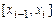. Очевидно, что возможна аппроксимация функции полиномом некоторой степени. Воспользуемся интерполяционным полиномом Ньютона второй степени для решения данной задачи в следующем виде

. (5.38)

Таким образом, на отрезке интеграл от заменяется на интеграл от (рисунок 5.5). Для того чтобы определить неизвестные коэффициенты этого полинома необходимо знать значения в трех точках, чем и определяется длина интервала.

Определим неизвестные коэффициенты , и . Для интерполяционных полиномов их значения в узлах совпадают со значением интерполируемой функции. Получаем

(5.39)

где, как и прежде, . Введем новую переменную , тогда полином (5.38) примет вид

.

Вычислим интеграл от полинома

(5.40)

Это соотношение представляет собой иллюстрацию метода Ньютона-Котеса второго порядка. Обычно его называют методом Симпсона или методом парабол. Совершенно очевидно, что рассмотренные простейшие методы вычисления интегралов (методы правых и левых прямоугольников и трапеций) представляют собой соответственно методы Ньютона-Котеса нулевого и первого порядка. При этом ясно, что формулы Ньютона-Котеса точны для многочленов степени 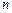, которые определяют количество интервалов разбиения интегрируемого отрезка.

Рисунок 5.5. Метод Ньютона-Котеса второго порядка (метод Симпсона)

Поставим следующую задачу: при заданном количестве узлов (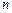 интервалов) построить квадратурную формулу, точную для многочленов наиболее высокой степени. Фактически это означает, что необходимо выбрать полином интерполяции и минимизировать погрешность вычисления . В результате мы должны получить коэффициенты полинома и координаты узлов интегрирования. Метод вычисления интегралов типа (5.29) называется методом Гаусса или методом наивысшей алгебраической точности.

Для того чтобы пределы интегрирования не зависели от пределов интегрирования, линейным преобразованием переменной 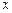осуществляется переход к стандартным пределам интегрирования относительно новой переменной ,

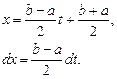(5.41)

Тогда интеграл (5.29) будет иметь вид . (5.42)

Здесь представляет собой некоторый полином степени вида

. (5.43)

Квадратурная формула (5.31) будет иметь вид

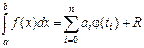(5.44)

и будет точна (т.е. погрешность ) для многочленов степени тогда и только тогда, когда она точна для функций , , ,..., . 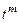Это эквивалентно тому, что узлы 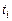и веса 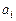должны удовлетворять системе нелинейных уравнений , (5.45)

где 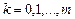. Можно показать, что система (5.45) имеет единственное решение ,..., , ,..., , 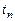тогда и только тогда, когда число уравнений совпадает с числом неизвестных, т.е. в случае .

В качестве примера рассмотрим построение квадратурной формулы Гаусса с двумя узлами (рисунок 5.6). В этом случае , а , т.е. формула будет точна для многочленов не выше третьей степени. Система (5.45) примет вид

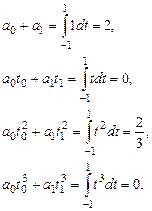(5.46)

Решая ее, находим, что , , . Таким образом находим, что квадратурная формула Гаусса точная для многочленов третьей степени будет иметь вид

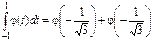. (5.47)

Рисунок 5.6. Метод Гаусса для двух узлов

Дата добавления: 2017-01-14