
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение краевой задачи для ОДУ
|
|
|
|
В отличие от задачи Коши краевые задачи предусматривают однозначное определение решения, используя значения неизвестной функции, ее первой производной или их линейной комбинации на границе рассматриваемой области. Ограничимся случаем одной переменной, тогда, если значения функции задано во внутренних точках области определения, то такую задачу называют внутренней краевой задачей, а, если на границе, то внешней краевой задачей. Среди таких задач существенную часть составляют задачи для дифференциальных уравнений второго порядка. Рассмотрим один из методов решения этих задач.
Пусть требуется найти решение дифференциального уравнения
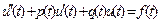 ,(7.24)
,(7.24)
на отрезке  , которое удовлетворяет краевым условиям:
, которое удовлетворяет краевым условиям:
 (7.25)
(7.25)
Построим сетку  на отрезке
на отрезке 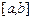 , на которой определим сеточные функции
, на которой определим сеточные функции  ,
,  и
и  , приближенное решение в виде сеточной функции будем, как и прежде, обозначать через
, приближенное решение в виде сеточной функции будем, как и прежде, обозначать через 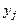 . Аппроксимируем производные, входящие в уравнения (7.24)-(7.25), со вторым порядком точности в результате получим разностную схему для краевой задачи:
. Аппроксимируем производные, входящие в уравнения (7.24)-(7.25), со вторым порядком точности в результате получим разностную схему для краевой задачи:
 , (7.26)
, (7.26)
с краевыми условиями
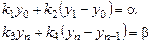 (7.27)
(7.27)
где  . Отметим без доказательства тот факт, что данная схема является устойчивой.
. Отметим без доказательства тот факт, что данная схема является устойчивой.
Введем обозначения
 ,
,  ,
, 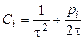 ,
,
для  и
и

для 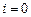 и
и  . Тогда система линейных алгебраических уравнений (7.26) – (7.27) запишется в виде:
. Тогда система линейных алгебраических уравнений (7.26) – (7.27) запишется в виде:
 (7.28)
(7.28)
или в матричном виде:
 , (7.29)
, (7.29)
где  – трехдиагональная матрица, а
– трехдиагональная матрица, а  и
и  – вектор столбцы. Решение этой системы осуществляется, как правило, методом прогонки. Численная реализация метода полностью основывается на решении СЛАУ с трехдиагональной матрицей коэффициентов.
– вектор столбцы. Решение этой системы осуществляется, как правило, методом прогонки. Численная реализация метода полностью основывается на решении СЛАУ с трехдиагональной матрицей коэффициентов.
8.1. Решения дифференциальных уравнений первого порядка
Существует много задач о распространении частиц в веществе, например, определение теплопроводности в газах, обусловленное диффузией атомов и электронов. Такие уравнения приводят к уравнению переноса, простейшее из которых приводит к линейному дифференциальному уравнению
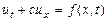 ,(8.3)
,(8.3)
где 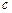 – скорость переноса. Для полной определенности решения зададим начальные и граничные условия
– скорость переноса. Для полной определенности решения зададим начальные и граничные условия
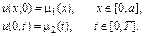 (8.4)
(8.4)
Построим разностную схему решения этого уравнения, которую называют схемой бегущего счета. Введем прямоугольную сетку, образованную пересечением прямых линий:
 ,
,  .
.
Точку 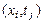 будем называть узлом, а множество узлов с одним и тем же значением индекса
будем называть узлом, а множество узлов с одним и тем же значением индекса  -слоем (
-слоем ( -тым слоем). Положим
-тым слоем). Положим 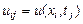 – это значение функции
– это значение функции 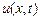 в узле
в узле 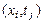 . Проведем аппроксимацию производных в уравнении (8.3), при этом будем полагать, что
. Проведем аппроксимацию производных в уравнении (8.3), при этом будем полагать, что 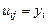 , а
, а  , получим следующие численные схемы
, получим следующие численные схемы 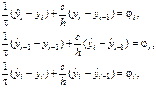 (8.5)
(8.5)
где наилучшим приближением правой части (8.3) будет
 .
.
(8.6)
Будем называть шаблоном разностной схемы множество узлов, входящих в соответствующую формулу. Шаблоны этих схем представлены на рисунке 8.1.
Формально первая из схем (8.5) является явной, а остальные две – неявными, фактически же они ведут себя как явные. Действительно, во всех этих задачах значение на следующем слое явно выражается через значения на предыдущем. Решение на нулевом слое определяется из начальных условий 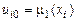 , на первом слое значения
, на первом слое значения 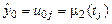 известны в силу граничного условия, далее вычисляем все значения на первом слое
известны в силу граничного условия, далее вычисляем все значения на первом слое  . Затем, зная решение на первом слое, точно так же вычисляем его на втором слое и т.д.
. Затем, зная решение на первом слое, точно так же вычисляем его на втором слое и т.д.
Отметим, что явная схема пригодна для расчета на полу- или бесконечной прямой, неявные схемы бегущего счета к такой задаче неприменимы. Однако на практике задача для уравнения переноса в неограниченной области почти не встречается.
Исследуем устойчивость разностной схемы, используя принцип максимума. Пусть  и
и  – решения одной и той же разностной схемы, отвечающие разным начальным условиям. Разностная схема называется устойчивой (равномерно устойчивой), если выполняется условие
– решения одной и той же разностной схемы, отвечающие разным начальным условиям. Разностная схема называется устойчивой (равномерно устойчивой), если выполняется условие
 ,(8.7)
,(8.7)
где  , а
, а 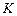 не зависит от
не зависит от  и
и  , при этом норма определяется как максимум модуля. Справедливо следующее утверждение. Если при всех
, при этом норма определяется как максимум модуля. Справедливо следующее утверждение. Если при всех 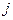 выполняется условие
выполняется условие
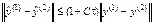 , (8.8)
, (8.8)
где  , а
, а 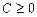 , то соответствующая разностная схема равномерно устойчива.
, то соответствующая разностная схема равномерно устойчива.
Условие (8.8) означает, что если на некотором слое имеется ошибка 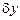 , то при переходе на следующий слой норма
, то при переходе на следующий слой норма 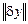 возрастет не более чем в
возрастет не более чем в  раз. Для перехода от
раз. Для перехода от  к
к  надо сделать число шагов по времени, определяемое равенством
надо сделать число шагов по времени, определяемое равенством  . При этом ошибка возрастет не более чем в
. При этом ошибка возрастет не более чем в 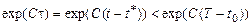 раз. Отсюда следует, что
раз. Отсюда следует, что
 ,(8.9)
,(8.9)
где  , то есть выполняется (8.7).
, то есть выполняется (8.7).
Из соотношения (8.8) видно, что если константа  велика, то, хотя схема формально устойчива, фактически ошибка может сильно возрастать в ходе расчетов, т.е. схема является слабо устойчивой. Очевидно, чем больше промежуток времени
велика, то, хотя схема формально устойчива, фактически ошибка может сильно возрастать в ходе расчетов, т.е. схема является слабо устойчивой. Очевидно, чем больше промежуток времени  , на котором ищется решение, тем меньше величина
, на котором ищется решение, тем меньше величина  обеспечивает устойчивость расчета. При больших
обеспечивает устойчивость расчета. При больших  схема будет устойчивой лишь при
схема будет устойчивой лишь при 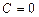 . Поэтому при проверке выполнения достаточного условия устойчивости обычно полагают
. Поэтому при проверке выполнения достаточного условия устойчивости обычно полагают 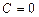 .
.
Внесем для однородного уравнения явной схемы на слое j ошибку в вычисления 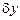 , тогда ошибка
, тогда ошибка  на слое (j+1) будет определяться из уравнения
на слое (j+1) будет определяться из уравнения
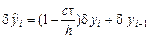 . (8.10)
. (8.10)
Откуда

(8.11)
и получаем критерий равномерной устойчивости схемы
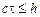 .(8.12)
.(8.12)
Это так называемое условие Куранта. Так как схема является устойчивой не при всех значениях  , то она является условно устойчивой. Аналогичные рассуждения для обеих неявных схем приводят к выводу о том, что они устойчивы при любых соотношениях
, то она является условно устойчивой. Аналогичные рассуждения для обеих неявных схем приводят к выводу о том, что они устойчивы при любых соотношениях  , таким образом, эти схемы являются безусловно устойчивыми.
, таким образом, эти схемы являются безусловно устойчивыми.
8.2. Решения дифференциальных уравнений параболического типа
Рассмотрим уравнение теплопроводности, описывающее распространение тепла в однородном стержне
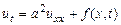 ,
,
(8.13)
где функция  определяет температуру стержня в сечении
определяет температуру стержня в сечении 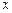 в момент времени
в момент времени  ,
,  , а
, а 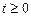 . Здесь
. Здесь 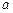 – коэффициент температуропроводности,
– коэффициент температуропроводности,  – заданная функция, равная нулю, если внутри стержня отсутствуют источники тепла. Нетрудно убедится, используя канонический вид дифференциального уравнения (8.1) и выражение для вычисления дискриминанта (8.2), что это уравнение является дифференциальным уравнением параболического типа.
– заданная функция, равная нулю, если внутри стержня отсутствуют источники тепла. Нетрудно убедится, используя канонический вид дифференциального уравнения (8.1) и выражение для вычисления дискриминанта (8.2), что это уравнение является дифференциальным уравнением параболического типа.
Построим разностную схему решения дифференциального уравнения (8.13) с начальным условием и граничными условиями
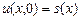 ,
,  .(8.14)
.(8.14)
Как и раньше введем прямоугольную сетку, на которой определим 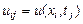 и
и 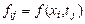 . Заменим производные
. Заменим производные  и
и  разностными отношениями, причем производную
разностными отношениями, причем производную  будем аппроксимировать в слое j, в результате получим разностную схему
будем аппроксимировать в слое j, в результате получим разностную схему
 ,(8.15)
,(8.15)
для 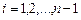 . С начальными и граничными условиями
. С начальными и граничными условиями
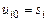 ,
, 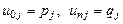 (8.16)
(8.16)
при  . Данной схеме соответствует следующий шаблон
. Данной схеме соответствует следующий шаблон
Если же производную  аппроксимировать разностным отношением не на слое j, а на слое (j +1), то получим разностную схему
аппроксимировать разностным отношением не на слое j, а на слое (j +1), то получим разностную схему
(8.17)
В этом случае 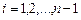 с теми же начальными и граничными условиями, что и для схемы (8.15). Этой схеме соответствует шаблон
с теми же начальными и граничными условиями, что и для схемы (8.15). Этой схеме соответствует шаблон
В схеме (8.15) в каждом уравнении содержится только одно значение функции на следующем слое. Это значение явно выражается через значения функции на данном слое, поэтому эта схема называется явной. Схема (8.17) содержит в каждом уравнении несколько неизвестных значений функции на новом слое, такая схема называется неявной. Перепишем схему (8.17) в следующем виде
с граничными условиями
 для
для 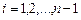 . На каждом слое с номером
. На каждом слое с номером 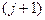 схема (8.18) представляет собой систему линейных алгебраических уравнений для определения величин
схема (8.18) представляет собой систему линейных алгебраических уравнений для определения величин 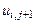 , правые части этих уравнений известны, поскольку содержат значения решения в предыдущем слое
, правые части этих уравнений известны, поскольку содержат значения решения в предыдущем слое 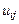 и значения известной функции
и значения известной функции  . Пусть
. Пусть  ,
,  и
и 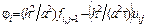 . Тогда уравнения (8.18) преобразуются к виду
. Тогда уравнения (8.18) преобразуются к виду
 при
при 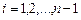 , (8.19)
, (8.19)
Эта система линейных алгебраических уравнений с трехдиагональной матрицей коэффициентов, она может быть решена методом прогонки.
Введем обозначения  ,
,  ,
,  и рассмотрим однородное дифференциальное уравнение. Неявная схема будет представлена уравнениями:
и рассмотрим однородное дифференциальное уравнение. Неявная схема будет представлена уравнениями:
 (8.20)
(8.20)
при 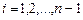 , а явная схема:
, а явная схема:
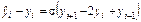 (8.21)
(8.21)
или
 . (8.22)
. (8.22)
Исследуем устойчивость схем вычисления с использованием принципа максимума. Внесем ошибку 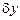 на исходном слое, тогда ошибка
на исходном слое, тогда ошибка  на новом слое будет удовлетворять для явной схемы равенству
на новом слое будет удовлетворять для явной схемы равенству
 ,
,
из которого следует, что
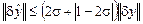 .
.
Решая неравенство
 ,
,
получаем условие устойчивости явной схемы
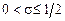 . (8.23)
. (8.23)
Для неявной схемы, аналогично рассуждая, получаем равенство
 ,откуда следует, что неравенство
,откуда следует, что неравенство

выполняется при всех  . Это означает, что неявная схема является безусловно устойчивой Приведем фрагмент m-файла для нахождения решения по явной схеме (8.15). Температура на концах стержня считается постоянной. Предварительно должно быть задано начальное распределение температуры в стержне – вектор
. Это означает, что неявная схема является безусловно устойчивой Приведем фрагмент m-файла для нахождения решения по явной схеме (8.15). Температура на концах стержня считается постоянной. Предварительно должно быть задано начальное распределение температуры в стержне – вектор  размерности
размерности 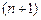 . Вектор
. Вектор  , также имеющей размерность
, также имеющей размерность 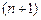 , задает координаты точек стержня, в которых рассчитывается температура. Параметр
, задает координаты точек стержня, в которых рассчитывается температура. Параметр  определяет значение величины
определяет значение величины  . Значения функции вычисляются до слоя
. Значения функции вычисляются до слоя  , кроме того, запоминается распределение температур в слоях
, кроме того, запоминается распределение температур в слоях 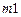 ,
,  ,
,  (
( ). На графике показывается начальное распределение температуры, распределение температуры в промежуточных слоях и распределение температуры в последнем просчитанном слое с номером
). На графике показывается начальное распределение температуры, распределение температуры в промежуточных слоях и распределение температуры в последнем просчитанном слое с номером 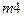
8.3. Решение дифференциальных уравнений эллиптического типа
Рассмотрим в качестве примера задачу об определении электростатического потенциала и напряженности электрического поля в бесконечном металлическом желобе прямоугольного сечения (рис.8.2). Верхняя стенка желоба имеет потенциал  , а остальные стенки заземлены и находятся под нулевым потенциалом. Необходимо найти функцию
, а остальные стенки заземлены и находятся под нулевым потенциалом. Необходимо найти функцию 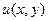 , описывающую распределение потенциала в этой области.
, описывающую распределение потенциала в этой области.
Из электростатики известно, что распределение потенциала  удовлетворяет уравнению Пуассона.
удовлетворяет уравнению Пуассона.
 ,
,
(8.24)
которое в декартовой системе координат будет иметь вид
 .(8.25)
.(8.25)
Функция  определяет плотность зарядов в исследуемой области. Необходимо найти решение уравнения (8.24), удовлетворяющее граничным условиям
определяет плотность зарядов в исследуемой области. Необходимо найти решение уравнения (8.24), удовлетворяющее граничным условиям
 (8.26)
(8.26)
После определения потенциала можно найти и напряженность электрического поля  , используя соотношение
, используя соотношение
 .
.
Поставленная задача является частным случаем задачи Дирихле, когда необходимо найти решение дифференциального уравнения в частных производных в замкнутой области 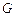 при заданном распределении искомой функции
при заданном распределении искомой функции 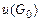 на границе этой области
на границе этой области  . В случае прямоугольной области и отсутствие электрических зарядов в области
. В случае прямоугольной области и отсутствие электрических зарядов в области 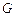 для граничных условий (8.26) решение можно получить аналитически, методом разделения переменных. Однако аналитическое решение не обобщается на более сложные границы и граничные условия. В некоторых задачах аналитические решения настолько громоздки, что невозможно осуществить их анализ без проведения численных расчетов, в таком случае численные решения могут оказаться более предпочтительными вследствие их универсальности.
для граничных условий (8.26) решение можно получить аналитически, методом разделения переменных. Однако аналитическое решение не обобщается на более сложные границы и граничные условия. В некоторых задачах аналитические решения настолько громоздки, что невозможно осуществить их анализ без проведения численных расчетов, в таком случае численные решения могут оказаться более предпочтительными вследствие их универсальности.
Для представления производных введем, как и раньше, прямоугольную сетку, разбивая исследуемую область вдоль оси 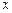 на
на  частей, а вдоль
частей, а вдоль  на
на 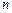 . Приближенные значения искомой функции в узле будут определяться значениями функции в соседних узлах. Для этого представим вторые производные в виде разностного аналога
. Приближенные значения искомой функции в узле будут определяться значениями функции в соседних узлах. Для этого представим вторые производные в виде разностного аналога
 ,(8.28)
,(8.28)
 (8.29)
(8.29)
где  и
и  – шаг сетки по координатам
– шаг сетки по координатам 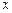 и
и  , соответственно, а
, соответственно, а  . Откуда
. Откуда
Это один из простейших шаблонов, часто называемый шаблоном типа «крест», будет иметь вид:
После преобразований (8.30) получаем систему уравнений относительно 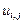 :
:
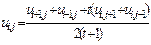 ,(8.31)
,(8.31)
где  . Для квадратной сетки, которая наиболее удобна для вычислений, формула упрощается, и ее знаменатель будет равен четырем. Система (8.31) является неявной и обычно решается итерационными методами, например методом Зейделя. Итерационный процесс завершается при выполнении в каждом узле сетки условия
. Для квадратной сетки, которая наиболее удобна для вычислений, формула упрощается, и ее знаменатель будет равен четырем. Система (8.31) является неявной и обычно решается итерационными методами, например методом Зейделя. Итерационный процесс завершается при выполнении в каждом узле сетки условия
 ,(8.32)
,(8.32)
где  – номер итерации, а
– номер итерации, а 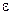 заданная погрешность вычисления потенциала.
заданная погрешность вычисления потенциала.
В качестве примера реализации программы рассмотрим случай соответствующий рисунку 8.2 при  , а длина стенок равна 1.
, а длина стенок равна 1.
|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 375; Нарушение авторских прав?; Мы поможем в написании вашей работы!