Решение дифференциальных уравнений гиперболического типа

К дифференциальным уравнениям гиперболического типа приводят задачи колебания струны, движения сжимаемого газа, распространение возмущения электромагнитных полей и многие другие. Рассмотрим одномерную задачу на примере решения задачи малых колебаний натянутой струны с распределенной по длине нагрузкой :

,

(8.33)

где – смещение струны относительно положения равновесия, а – константа, имеющая размерность скорости. Запишем начальные и краевые условия этой задачи (ограничимся краевыми условиями первого рода): 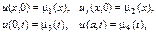(8.34)

где , а .

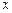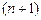Составим несложную, но достаточно эффективную разностную схему решения этой задачи. Выберем прямоугольную и для простоты равномерную сетку с шагом по времени равным ( узел) и по координате – ( узел). Введем обозначения , , и 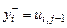. Аппроксимируя производные конечными разностями, получим трехслойную схему

(8.35)

или, вводя обозначение ,

. (8.36)

Здесь индекс 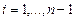, а граничные условия будут иметь вид

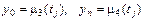. (8.37)

Данную схему по форме шаблона называют схемой «крест»:

(i,j+1)

Организация вычисления по этой схеме достаточно проста. На нулевом слое решение известно из начального условия с . На первом слое решение также можно вычислить, используя второе начальное условие в виде разностного уравнения,

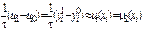, (8.38)

откуда

.(8.39)

Устойчивость этой схемы для однородного уравнения исследуем методом разделения переменных. Основная идея этого метода состоит в том, что исследуется решение на слое в виде комплексной гармоники и рассматривается ее поведение. При этом если модуль множителя (коэффициента) роста гармоники больше единицы при переходе со слоя на слой, то процесс считают неустойчивым, а соответствующий алгоритм не сходится. В соответствии с этим положим

(8.40)

где – номер гармоники, – множитель роста, а – мнимая единица. Подставим выражения (8.40) в уравнения (8.35) или (8.36) и сократим на , тогда получим уравнения для определения множителя роста:

. (8.41)

Условием устойчивости является . По теореме Виета произведение корней этого уравнения 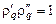. Следовательно, условие устойчивости может быть выполнено, если 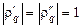. Для уравнения с действительными коэффициентами это означает, что корни образуют комплексно сопряженную пару, это означает, что дискриминант уравнения не должен быть положительным:

.

(8.42)

Чтобы это условие выполнялось для любых гармоник, необходимо и достаточно соблюдение условия Куранта 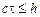. Таким образом, схема «крест» условно устойчива.

Построим более сложную, но хорошую схему, которая устойчива при любых значениях . В схеме решения (8.35) вторая производная по координате аппроксимирована в слое с номером , составим уравнение, в котором эта производная представлена в виде суммы с весами 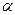в слоях , и :

(8.43)

Для того чтобы все веса были неотрицательны, необходимо потребовать . В граничных узлах решение определяется из краевых условий, организация счета аналогична схеме «крест». Кроме этого, данная схема является неявной, при построении расчетов относительно получаем систему линейных алгебраических уравнений с трехдиагональной матрицей коэффициентов.

Исследуем устойчивость этой схемы методом разделения переменных. Делая подстановку (8.40), получаем уравнение для множителя роста:

,(8.44)

где

На основании тех же рассуждений, что и для схемы крест, можно сделать вывод: устойчивость будет только при комплексно сопряженных корнях, т.е. при . Отсюда вытекает условие устойчивости схемы:

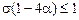.(8.45)

Из этого неравенства видно, что при схема – условно устойчива, а при схема – безусловно устойчива. Отметим, что при 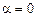схема (8.43) переходит в схему крест.

Дата добавления: 2017-01-14