Расчет замкнутого контура скорости с двухмассовым упругим электромеханическим объектом и подчиненным управлением

РАСЧЕТ МОДАЛЬНОЙ ЭЛЕКТРОМЕХАНИЧЕСКОЙ СЛЕДЯЩЕЙ СИСТЕМЫ С ДВУХМАССОВЫМ УПРУГИМ МЕХАНИЧЕСКИМ ОБЪЕКТОМ И НАБЛЮДАТЕЛЕМ

Пример выполнения работы.

Дано:

, , , , , , , ,

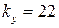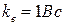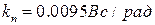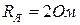Примем в качестве исходного двухмассовый упругий электромеханический объект с зазором, замкнутый по скорости 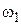с контурным П-регулятором и являющийся внутренним контуром двухконтурной электромеханической системы (см. рисунок 1). Его дифференциальные уравнения имеют вид:

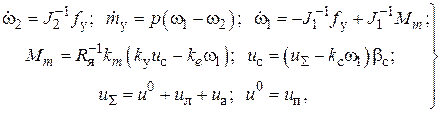(1)

где 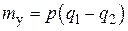– упругий момент, возникающий при деформации в упругой связи при отсутствии зазора; 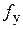– упругий момент, описываемый при учете зазора 2d в упругой связи нелинейной (недифференцируемой) функцией вида

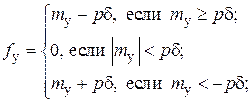(2)

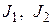– соответственно, момент инерции двигателя и момент инерции механизма нагрузки с учетом его приведения к вращению двигателя; p – коэффициент упругости (жесткости упругой связи); 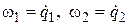– соответственно, угловые скорости первого и второго дисков 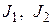; – настраиваемый коэффициент контурного П-регулятора скорости (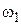); – известное программное (задающее) воздействие (для внутреннего контура скорости это выходной сигнал регулятора РП); 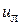и – соответственно, линейное и адаптивное управления, подлежащие определению.

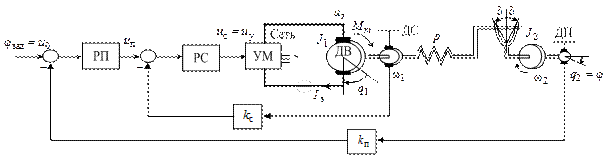
Рисунок 1 - Двухмассовый нелинейный упругий электромеханический объект с подчиненным управлением

Таким образом, описание контура скорости электромеханической следящей системы с двухмассовым упругим механическим объектом исчерпывается (с учетом принятых ранее допущений) системой нелинейных дифференциальных уравнений (1), (2) третьего порядка, записанных в так называемой скоростной форме уравнений упругого объекта. Кроме того, считаем, что в общем случае моменты инерции, отнесенные к двигателю и нагрузке, а также коэффициент жесткости являются неизвестными и нестационарными (функциями времени):

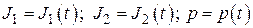, (3)

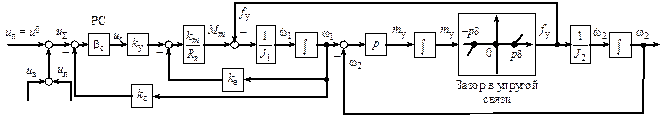
Рисунок 2 - Детализированная структурная схема замкнутого по первой скорости двухмассового упругого электромеханического объекта с зазором в упругой связи (1), (2)

Замечание. В дальнейших исследованиях будем пренебрегать нелинейностью и нестационарностью уравнений (1)÷(3) исходного упругого объекта (1)÷(3) и будем рассматривать его линейное и стационарное приближение с некоторыми усредненными постоянными параметрами:

. (5)

С учетом обозначений (5) и пренебрегая в уравнениях (1), (2) зазором ( и ) запишем линейное стационарное приближение контура скорости с упругим механическим объектом в виде:

(6)

Введем следующие обозначения:

(7)

С учетом введенных обозначений перепишем линеаризованные уравнения (6) с усредненными параметрами (7) в компактной форме

и для удобства представим их в векторно-матричной записи:

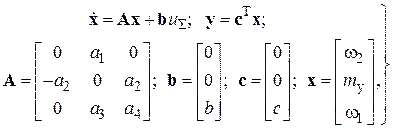(8)

где 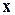– вектор состояния линеаризованного объекта (6); 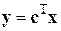– уравнение измерения; 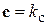(здесь доступной измерению с помощью датчика скорости ДС считается первая скорость ).

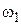Примем дифференциальную линейную систему (8) с параметрами (7) в качестве исходного расчетного объекта управления.

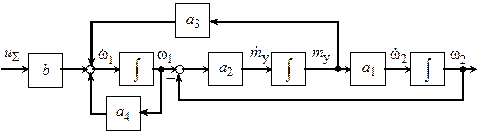
Рисунок 3 - Детализированная структурная схема замкнутого по первой скорости линеаризованного двухмассового упругого электромеханического объекта (6)–(8)

Числовой расчет объекта управления выполним по формулам (7), приняв следующие числовые значения параметров (см. задание):

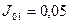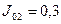кгм²; кгм²;

Нм/рад; Ом;

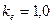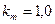Вс; Вс;

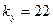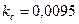; Вс/рад;

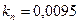В/рад; 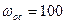рад/с;

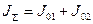= 0,35 (кгм²); рад/с;

; .

Расчет контурных регуляторов 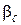, 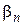выполним по формулам подчиненного управления, справедливым для жесткого объекта (при пренебрежении упругой связью, когда - велико, или :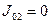

; .

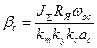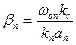Получаем:

• значения контурных регуляторов , :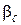

;

;

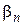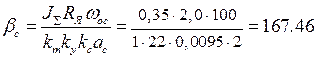• значения параметров (7) дифференциальной линейной системы (8):

Запишем дифференциальную линейную систему (8) в численном виде:

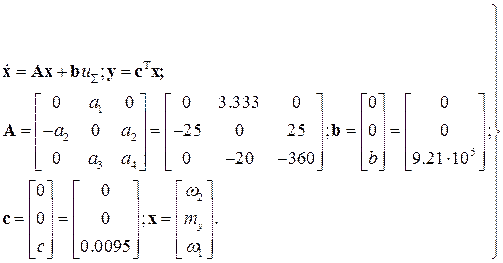
Сначала построим объект (6), (7) без учета упругих свойств, упрощая их и получая систему уравнений трехконтурной следящей системы с жестким объектом вида:

Далее построим и проведем исследования двухконтурной следящей системы с жестким объектом, принимая в ней , , :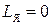

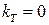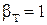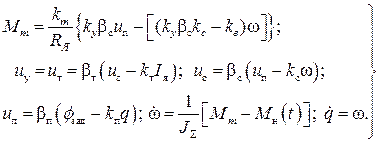
Получим переходный процесс вида (см. рисунок 4). На рисунке 5 представлен график переходного процесса в двухконтурной следящей системе с жестким объектом и подчиненным регулированием.

Рисунок 4 - Переходный процесс в двухконтурной следящей системе с жестким объектом и подчиненным регулированием.

а б

Рисунок 5 - Переходный процесс в системе с двухмассовым упругим объектом с подчиненным регулированием: а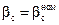) при , ; б) при , .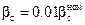

Дата добавления: 2015-07-13