Адаптивно-линейное управление с параметрической настройкой

Построение структуры адаптивно-линейной системы с параметрической настройкой рассмотрим в рамках прямого адаптивного управления с эталонной моделью (24). Искомое управление является составной функцией вида, показанного в (1), линейная составляющая управления 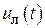вычисляется по формулам (22), (15), оценки переменных вырабатываются наблюдателем (16), (17), (21).

Адаптивное управление с параметрической настройкой строится в соответствии с методикой, изложенной в главе 7, и имеет следующий вид:

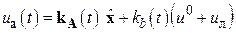, (26)

или в скалярной форме (мажорирующую функцию приравниваем к единице):

,

где – вектор-строка настраиваемых коэффициентов, а 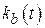– настраиваемый входной коэффициент адаптивного закона (26).

Алгоритмы настройки параметров адаптивного управления (26) выражаются дифференциальными уравнениями вида

(27)

или в скалярной форме:

(28)

где ; ,, , i = 1, 2, 3, – положительные коэффициенты усилений цепей настроек.

Детализированная структурная схема адаптивного закона управления (26) с алгоритмами параметрической настройки (27) для двухмассового упругого объекта представлена на рисунке 11.

Рисунок 11 - Детализированная структурная схема адаптивного закона управления (26) с алгоритмами параметрической настройки (27) для двухмассового упругого объекта

Ниже приведем примеры переходных процессов в двухмассовом упругом электромеханическом объекте с адаптивно-модальной системой управления при следующих значениях коэффициентов настроек параметрической адаптации: ; ; - нижняя строка матрицы Р, вычисляющийся из уравнения Ляпунова ()

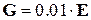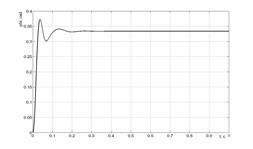
Рисунок 12 - Переходный процесс в системе двухмассового упругого объекта с адаптивно-модальным регулятором.

Проведем исследование двухмассового упругого электромеханического объекта (6)-(8) с адаптивно-модальным управлением (9),(15), (24), (26), (27), (28) изменяя только 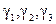и 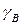в уравнениях параметрической настройки (27), (28):

1) ,

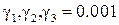Рисунок 13 - Переходный процесс в системе с двухмассовым упругим объектом с подчиненным регулированием , и адаптивно-модальным управлением с параметрической настройкой и эталонной моделью при изменении параметров

n) ,

Рисунок 14 - Переходный процесс в системе с двухмассовым упругим объектом с подчиненным регулированием , и адаптивно-модальным управлением с параметрической настройкой и эталонной моделью при изменении параметров.

Проведем исследование двухмассового упругого электромеханического объекта (6) с адаптивно-модальным управлением (9)-(15), (26) изменяя только и :

1) ,

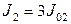Рисунок 15 - Переходный процесс в системе с двухмассовым упругим объектом с адаптивно-модальным управлением при изменении параметров объекта.

k) ,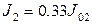

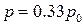
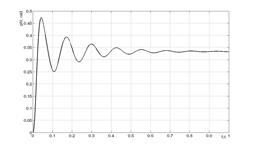
Рисунок 16 - Переходный процесс в системе с двухмассовым упругим объектом с адаптивно-модальным управлением при изменении параметров объекта.

Дата добавления: 2015-07-13