Расчет линейного (модального) управления двухмассовым упругим электромеханическим объектом

Задача построения линейной составляющей 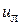управления объекта (8) – обеспечить динамику (быстродействие и вид переходных процессов по управлению) замкнутого контура скорости электромеханической следящей системы с линеаризованным упругим двухмассовым объектом (8) с усредненными параметрами (7), близкую к предельной динамике замкнутого «оптимизированного» контура скорости с жестким объектом и правильно настроенным П-регулятором с максимально достижимой полосой пропускания 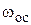и степенью демпфирования 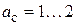. Здесь в качестве линейного управления, решающего поставленную задачу, примем модальное управление объектом (8) и рассчитаем его.

Модальный регулятор для объекта (8) имеет вид полной линейной обратной связи по состоянию

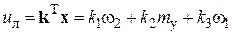, (9)

где вещественный вектор коэффициентов обратных связей рассчитывается из условия обеспечения любого наперед заданного желаемого распределения всех корней характеристического уравнения замкнутой системы (8), (9) с одним лишь ограничением: комплексные корни должны входить вместе со своими сопряженными значениями в силу вещественности элементов матриц 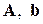. Характеристический многочлен замкнутой системы (8), (9) будет иметь вид

, (10)

и с учетом конкретного вида матриц 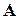, 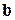в соответствии с выражением (8) в развернутой форме запишется:

. (11)

Желаемый характеристический многочлен замкнутой системы выберем в виде

, (12)

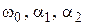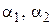где – положительные числа, характеризующие желаемую динамику ( – полосу пропускания, – форму переходных процессов по управлению) линеаризованной скоростной системы с упругим объектом, могут быть назначены произвольными. Например, целесообразно выбрать

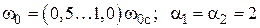, (13)

где 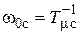, а выбор 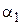и 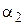равными 2 соответствует так называемому распределению корней 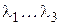многочлена (12) по Баттерворту:

.

Приравнивая коэффициенты при одинаковых степенях переменной в многочленах (11) и (12), получим алгебраическую систему относительно искомых коэффициентов 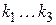обратных связей управления (9):

(14)

Однозначная разрешимость алгебраической системы (14) следует из полной управляемости упругого объекта (8), т.е. пары (), и окончательно получаем:

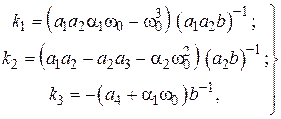(15)

Подставив численные значения параметров исходного расчетного объекта управления и приняв , получаем:

что и завершает расчет модального управления контура скорости электромеханической следящей системы с упругим двухмассовым объектом.

Расчет идентификатора состояния (наблюдателя) двухмассового электромеханического упругого объекта (по первой скорости)

Полученное модальное управление (9), (15) может быть реализовано только с помощью непосредственного измерения переменных 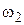, и 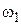, а так как переменные 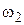и недоступны измерению с помощью датчиков, то для его осуществления необходимо использовать асимптотические оценки этих переменных, вырабатываемые наблюдателем. Построим его в виде асимптотического идентификатора состояния полного порядка для линеаризованного двухмассового упругого объекта (6)–(8), замкнутого по скорости П-регулятором.

Идентификатор (наблюдатель) по измерению первой скорости 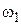расчетного объекта (6)–(8) имеет вид

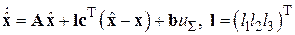, (16)

или в скалярной записи:

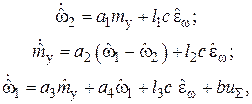(17)

где 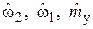– оценки переменных состояния объекта (6)–(8); 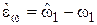– ошибка наблюдения; 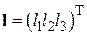– вектор коэффициентов обратных связей наблюдателя (16) по ошибке наблюдения измеряемой угловой скорости , ().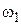

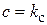Рисунок 6 - Детализированная структурная схема наблюдателя двухмассового упругого объекта (по первой скорости) (17)

Для расчета коэффициентов обратных связей 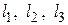составляем характеристический многочлен системы дифференциальных уравнений наблюдателя (16), замкнутого по ошибке наблюдения, в виде

, (18)

или с учетом уравнений наблюдателя (17) получим:

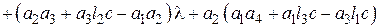. (19)

Желаемый характеристический многочлен наблюдателя, замкнутого по ошибке измерения 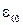, запишется в виде

. (20)

Приравнивая коэффициенты при одинаковых степенях в многочленах (19) и (20), получим систему алгебраических уравнений для коэффициентов , , , 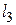разрешая которую относительно искомых коэффициентов, будем иметь

(21)

Заметим, что однозначная разрешимость полученной системы алгебраических уравнений следует из полной наблюдаемости упругого объекта (8), т. е. полной наблюдаемости пары А, с. Число в (20) характеризует желаемую полосу пропускания наблюдателя, кратную желаемой полосе пропускания (см. (12), (13)) упругого объекта (8), замкнутого модальным управлением (9.9); коэффициент кратности 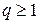(обычно принимают 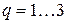); числа 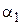, , 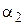как правило, принимаются такими же, как в многочлене (12), (13).

Рассчитаем значения коэффициентов обратных связей 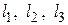наблюдателя, приняв :

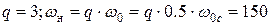Замечание 1. Структура наблюдателя полного порядка построена в соответствии с условием, что доступна измерению только одна переменная – угловая скорость исполнительного привода (обозначенная здесь ).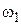

Замечание 2. Вообще говоря, измеряемые датчиками переменные могут быть исключены из структуры наблюдателя. В этом смысле размерность наблюдателя полного порядка избыточна, и может быть построен наблюдатель пониженного порядка, равного , где – полный порядок наблюдаемого объекта, а 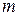– число измеряемых датчиками переменных. Такие наблюдатели пониженного порядка называются наблюдателями Луенбергера, и здесь не рассматриваются.

Дата добавления: 2015-07-13