Релеївське розсіювання

Релеївське або квазіпружне розсіювання часто називають явищем «центрального піку». Коли температура кристалу висока і кількість фононів достатньо велика, зіткнення фононів відбуваються часто і локальна термічна рівновага добре встановлена. В цьому випадку можна вважати, що розсіювання падаючого світла відбувається на флуктуаціях температури, або, що еквівалентно – ентропії. Це «термічне» розсіювання світла призводить до дифузійного релеївського центрального піку [5]. Добре відомо, що півширина піку зумовленого розсіюванням світла на флуктуаціях ентропії визначається як 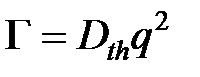, де 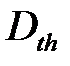– температуропровідність (відношення коефіцієнта теплопровідності до об’ємної теплоємності), а – величина хвильового вектора. Умови, що були перераховані вище, при яких справедлива теорія теплопровідності часто називають «гідродинамічним режимом» або «режимом зіткнень» [6]. У протилежному випадку, коли зіткнення між фононами відбуваються дуже рідко, теорія теплопровідності не працює і температура та ентропія не можуть бути визначеними локально. У цьому випадку потрібно брати до уваги нетермодинамічні процеси розсіювання; вважається, що розсіювання світла відбувається внаслідок послідовного створення та знищення декількох фононів (дво-фононне розсіювання світла) [6]. Цю обмежуючу умову часто називають «режимом без зіткнень». У загальному, критерієм застосовності гідродинаміки до системи є умова, коли 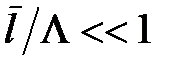, де 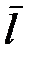– середня довжина вільного пробігу частинки, що входить до складу системи, а 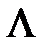– характеристична довжина. Величина називається «числом Кнудсена» і представляє собою обернене число кількості зіткнень на довжині 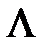. З використанням Kn, критерій гідродинамічного і режиму без зіткнень можна записати як і , відповідно. У випадку, коли будемо мати проміжний режим (для котрого, поки що, немає теорії розсіювання світла). Оскільки характеристична довжина в експериментах по розсіюванню світла визначається як , число Кнудсена при розсіюванні світла для фононного газу визначається як [7]. У кожному із перерахованих режимів можна вважати, що квазіпружне розсіювання світла відбувається на флуктуаціях фононної густини у кристалі [8]. І таке розсіювання світла можна характеризувати числом Кнудсена.

1.3. Мандельштам - бріллюенівське розсіювання світла

Мандельштам - бріллюенівське розсіювання (МБР) – це розсіювання світла, зумовлене дифракцією на пружній звуковій хвилі [9], тобто розсіювання відбувається на оптичних неоднорідностях, що викликані флуктуаціями тиску. Аналогічно як і при КР, у спектрі розсіяного світла виникають нові лінії, за частотою відмінні від , проте із меншим зміщенням. У загальному випадку в кристалі в заданому напрямку можуть розповсюджуватись з різними швидкостями три плоскі лінійно поляризовані пружні хвилі із взаємно-ортогональною поляризацією. Отже у спектрі розсіяного світла будуть спостерігатися три компоненти МБР.

Як схематично показано на рис. 1.2, у спектрі розсіяного світла можна виділити три області. Раманівські частоти , що зумовлені розсіюванням на оптичних фононах, займають інтервал 10 – 3000 см^‑1. Мандельштам - бріллюенівські спектри, котрі виникають внаслідок розсіювання на акустичних модах, знаходяться в інтервалі 1 – 0.05 см^–1. Релеївські спектри, що зумовлені розсіюванням на модах, котрі не поширюються, знаходяться в інтервалі 10⁹ – 10^–4 . На рис. 1.2. також показані типові області значення енергії та імпульсу в різних експериментах по розсіюванню. Видно, що при оптичному розсіюванні енергія змінюється значно сильніше, ніж імпульс [10]. Непружне розсіювання теплових нейтронів відбувається зі значною зміною імпульсу.

Вимірювання частотного зсуву компонент Мандельштама - Бріллюена дозволяє визначити швидкості поширення пружних хвиль, з яких можуть бути визначені пружні константи кристалів. Фотопружні константи можуть бути розраховані з вимірювання інтенсивності ліній в спектрах МБР. Використовуючи результати, отримані з розсіювання світла, тобто спектроскопічні данні, і термодинамічні величини, що одержані із безпосередніх вимірювань, можна порівняти і оцінити величини, які надзвичайно важко виміряти прямими методами.

Рис. 1.2. Схематична діаграма, що ілюструє область значень енергії, частоти та імпульсу, котрі перекриваються трьома експериментами по розсіюванню світла, а також при розсіюванні нейтронів.

Сьогодні дослідженню мандельштам - бріллюенівського розсіювання світла в найрізноманітних матеріалах присвячена чимала кількість робіт. Проте кристали ряду Sn(Pb)₂P₂S(Se)₆ цим методом дослідженні недостатньо. Так, одна із перших робіт по дослідженню цих кристалів із використанням методики мандельштам - бріллюенівського розсіювання, присвячена вивченню температурної поведінки швидкості та затухання повздовжніх звукових хвиль у кристалі 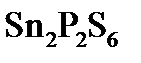вздовж двох кристалографічних напрямків [010] та [001]. У цій праці також проведено аналіз аномалій швидкості і затухання гіперзвуку в моделі Ландау - Халатнікова. Встановлено, що при досить непоганому описі температурної залежності затухання гіперзвуку в цій моделі, при цих же параметрах неможливо адекватно описати температурну поведінку швидкості гіперзвуку. У [11, 12, 13] було зроблено акцент на пружних властивостях кристалів Sn₂P₂S₆ та Sn₂P₂(S_0.72Se_0.28)₆. Проведено дослідження температурної залежності швидкості гіперзвуку при фазовому переході із параелектричної у сегнетоелектричну фазу кристалів. На основі цих даних було отримано повний набір пружних модулів кристалів. Всі попередні дослідження проводились в 90° геометрії (частота ~ 17 ГГц).

РОЗДІЛ 2 [A2]

СТРУКТУРА І ФІЗИЧНІ ВЛАСТИВОСТІ КРИСТАЛІВ (Pb_ySn_1-y)₂P₂S₆

Дата добавления: 2015-08-31