Методика експериментальних досліджень

Блок-схема спектрометра, що використовувався, представлена на рис. 3.1 Розсіювання Мандельштама-Бріллюена [18,19] збуджувалося гелій-неоновим лазером ЛГН-215 1 (довжина хвилі випромінювання l = 6328 Å) потужністю близько 50 мВт. Промінь світла від лазера проходить через пластинку l/2 для обертання площини поляризації та фокусується на зразок лінзою 2. Розсіяне під кутом 90° світло збирається об’єктивом 3 та фокусується на апертурну діа­фрагму 4. Після діафрагми світло збирається в паралельний пучок лінзою 5 і падає на інтерферометр Фабрі-Перо (ІФП) 7. Для забезпечення три­разового проходу розсіяного світла через інтерферометр встановлено дві трипльпризми 6. Світло, що пройшло, збирається лінзою 8 та фокусується на вихідну діафрагму 9. Далі встановлено лінзу 10, у фокальній площи­ні якої знаходиться фотокатод фотоелектронного помножувача (ФЕП) 11 типу ФЭУ-106. В даній установці реалізована фотоелектрична схема реє­страції методом «рахунку фотонів». Сигнал з ФЕП подається на електрофотометр 12, а далі на вхід «Y» двокоординатного самописця 13. Фокусні відстані всіх використаних лінз та діаметри діафрагм вибиралися для отримання найбільш високої різкості інтерференційної картини та інтенсивності.

У даній установці використаний плоский ІФП типу ИТ – 51 – 30, що сканується тиском. Коефіцієнт відбивання пластин інтерферометра r = 91.6%. Всі вимірювання провадилися при довжині бази інтерферометра D = 1.992мм, що відповідає області дисперсії 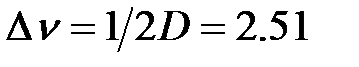см^–1. При даній обла­сті дисперсії та на довжині випромінювання гелій-неонового лазеру, роздільна здатність інтерферометра склала 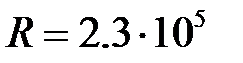, а різкість інтерференційних смуг біля 35, ширина апаратної функції – 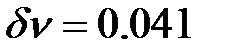см^–1. Для забезпечення сканування тиском інтерферометр сполу­чений з форвакуумним насосом 14. Оскільки зміна показника заломлення повітря (зміна оптичної довжини ходу променя в ІФП) відбувається ліній­но зі зміною тиску, до системи "форвакуумний насос — ІФП” включено інтегральний перетворювач тиску 15 типу ІПТА-0.1. Виводи даного пере­творювача підключені на вхід "X" самописця 13, що забезпечує лінійну розгортку спектру розсіювання.

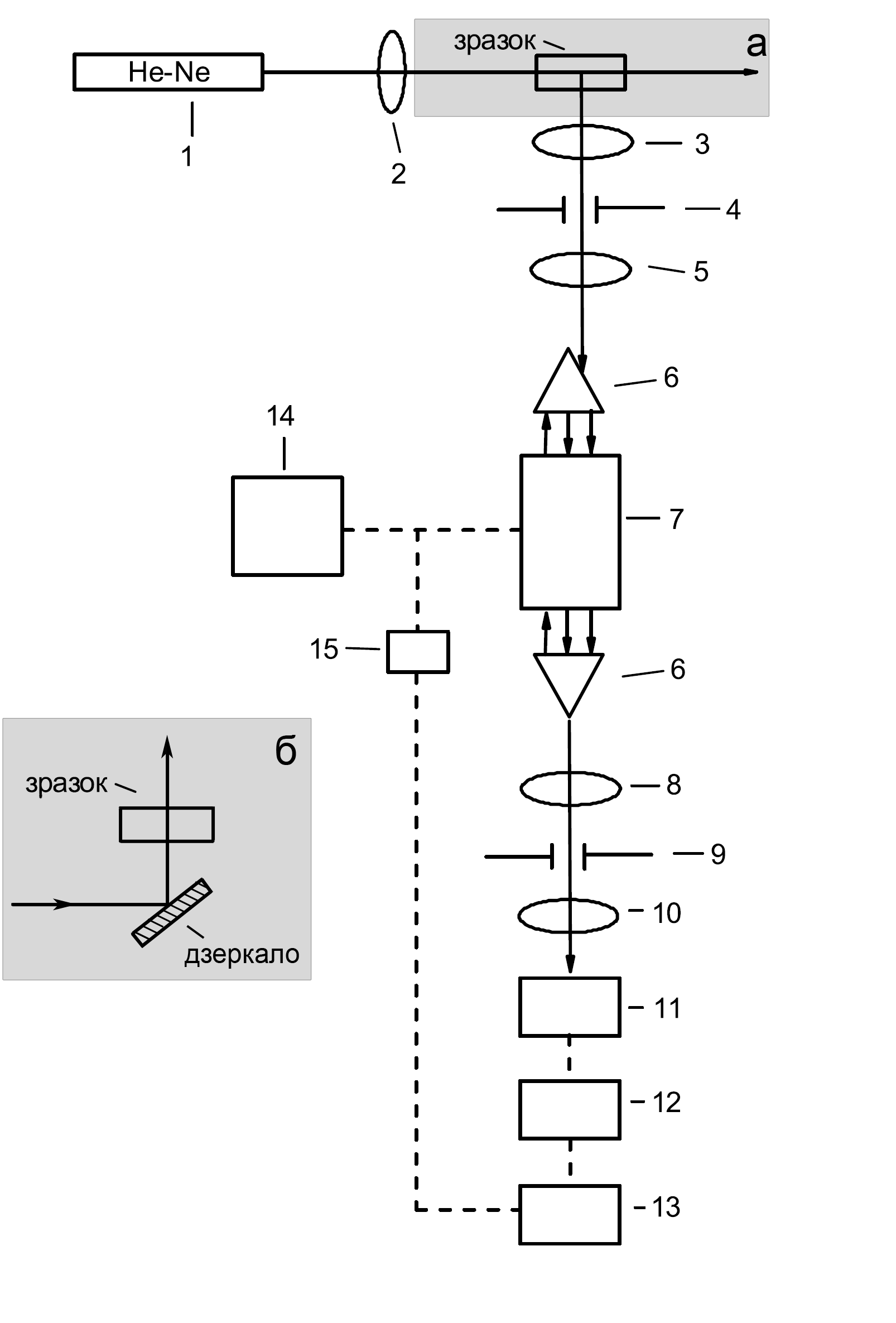
Рис. 3.1 Блок-схема експериментальної установки для дослідження мандельштам – бріллюенівського та релеївського розсіювання. а – 90˚ геометрія розсіювання; б – геометрія розсіювання назад (180˚).

що відповідає області дисперсії 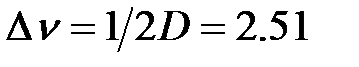см^–1. При даній обла­сті дисперсії та на довжині випромінювання гелій-неонового лазеру, роздільна здатність інтерферометра склала 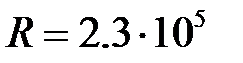, а різкість інтерференційних смуг біля 35, ширина апаратної функції – 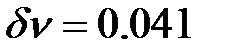см^–1. Для забезпечення сканування тиском інтерферометр сполу­чений з форвакуумним насосом 14. Оскільки зміна показника заломлення повітря (зміна оптичної довжини ходу променя в ІФП) відбувається ліній­но зі зміною тиску, до системи "форвакуумний насос — ІФП” включено інтегральний перетворювач тиску 15 типу ІПТА-0.1. Виводи даного пере­творювача підключені на вхід "X" самописця 13, що забезпечує лінійну розгортку спектру розсіювання.

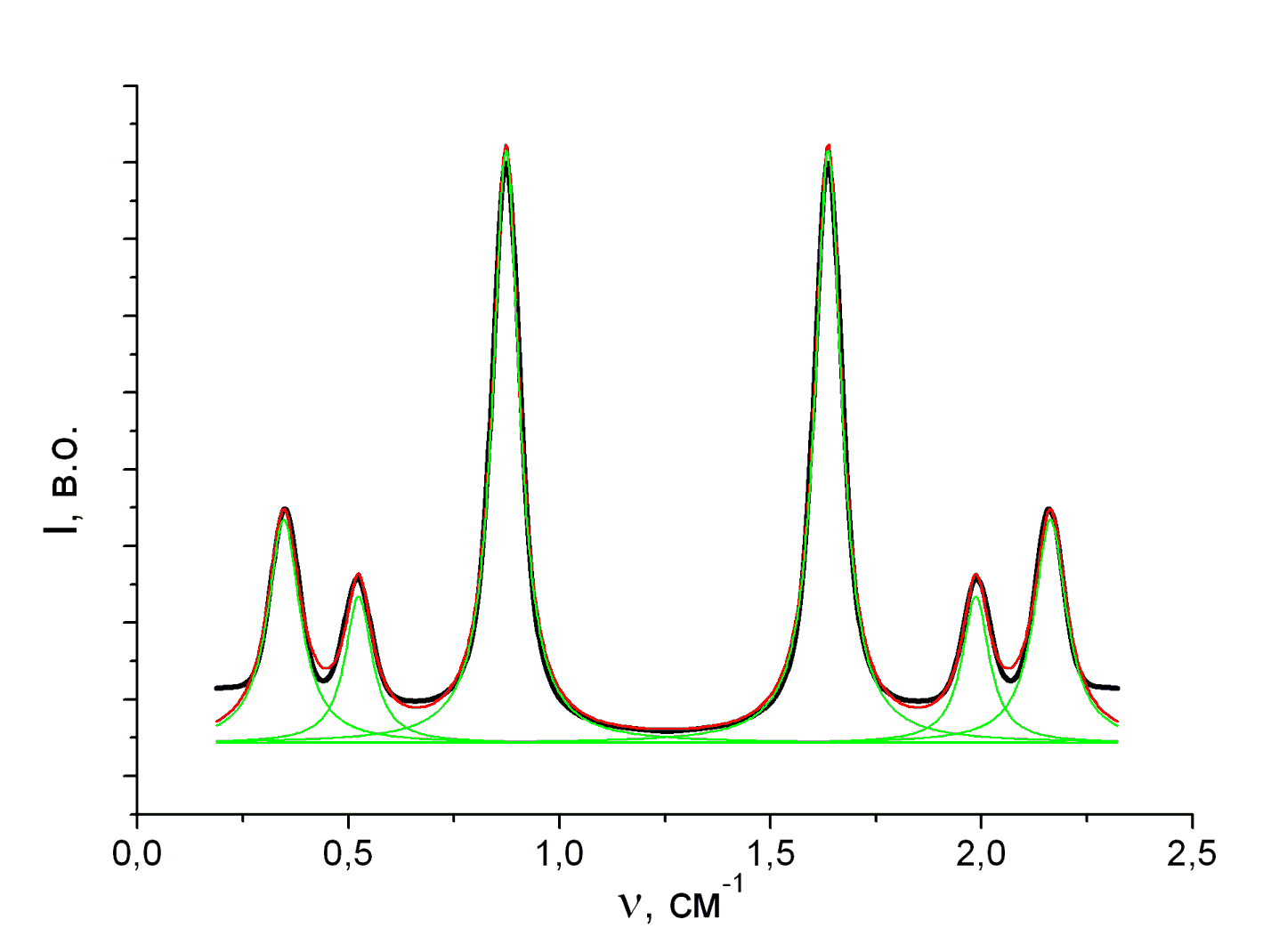
Рис.3.2 Розклад спектру МБР кристалу Sn₂P₂S₆ на контурні лінії Лоренца.

Для визначення швидкості та затухання гіперзвукових хвиль, спектри розсіювання розкладались на контурні лінії. Спектральні лінії мендельштам-бріллюенівського розсіювання описувалися формою Лоренца (рис. 3.2) Маючи частотний зсув та півширину 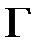(півширина на половині висоти) компонент МБР можна визначити швидкість 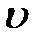та загасання 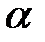звуку використовуючи наступні формули:

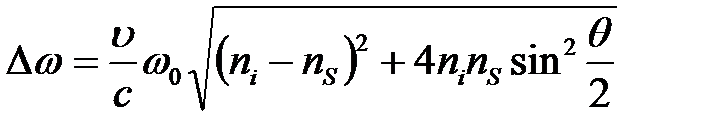, (3.13)

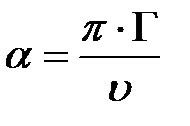(3.14)

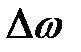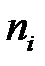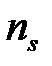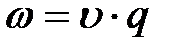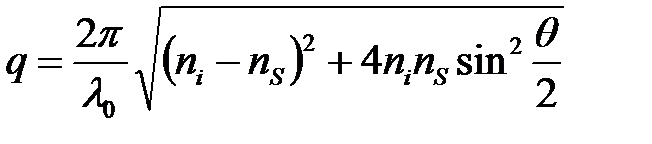де – частотний зсув компоненти МБР, – циклічна частота випромінювання гелій-неонового лазера, с – швидкість світла у вакуумі, – кут розсіювання, , – показники заломлення падаючого і розсіяного променів, відповідно. Оскільки , а , де 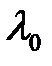– довжина хвилі He-Ne лазера, то змінюючи кут розсіювання, ми будемо змінювати хвильовий вектор розсіювання і як наслідок, частоту досліджуваного звуку. Тобто максимальний хвильовий вектор і максимальна частота будуть досягатися при розсіюванні назад (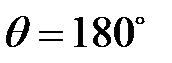), а мінімальні при розсіюванні вперед ().

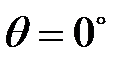Дослідження розсіювання світла проводилося в трьох геометріях: розсіювання під прямим кутом або 90˚ геометрія (рис. 3.1 вставка а), розсіювання назад або 180˚ геометрія (рис. 3.1 вставка б), та геометрія розсіювання 90А. У 90А геометрії світло падає під кутом 45˚ до поверхні зразка (див. рис. 3.3), при цьому хвильовий вектор розсіяного світла 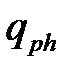знаходиться в площині зразка. Крім падаючого променя також наявний і відбитий промінь від внутрішньої стінки зразка з хвильовим вектором 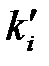, що приводить до спостереження у спектрі розсіювання менш інтенсивних ліній, котрі відповідають фононам з хвильовим вектором 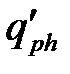і відносяться до «псевдо 180˚» геометрії (відхилення від 180˚ градусів може змінюватися в залежності від показника заломлення і для досліджуваних зразків складає менше 15˚).

Рис. 3.3 Схема розсіювання 90А геометрії: 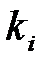, , 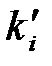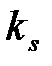– хвильові вектори падаючого, відбитого та розсіяного світла, відповідно; , 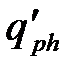– хвильові вектори акустичних фононів.

Приклад спектру в цій геометрії приведено на рисунку 3.4. Для 180˚ та 90А геометрій розсіювання формули для визначення швидкості можна записати таким чином:

(3.15)

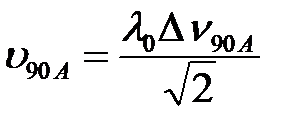(3.16)

Похибка визначення швидкості звуку з МБР не перевищує 3%.

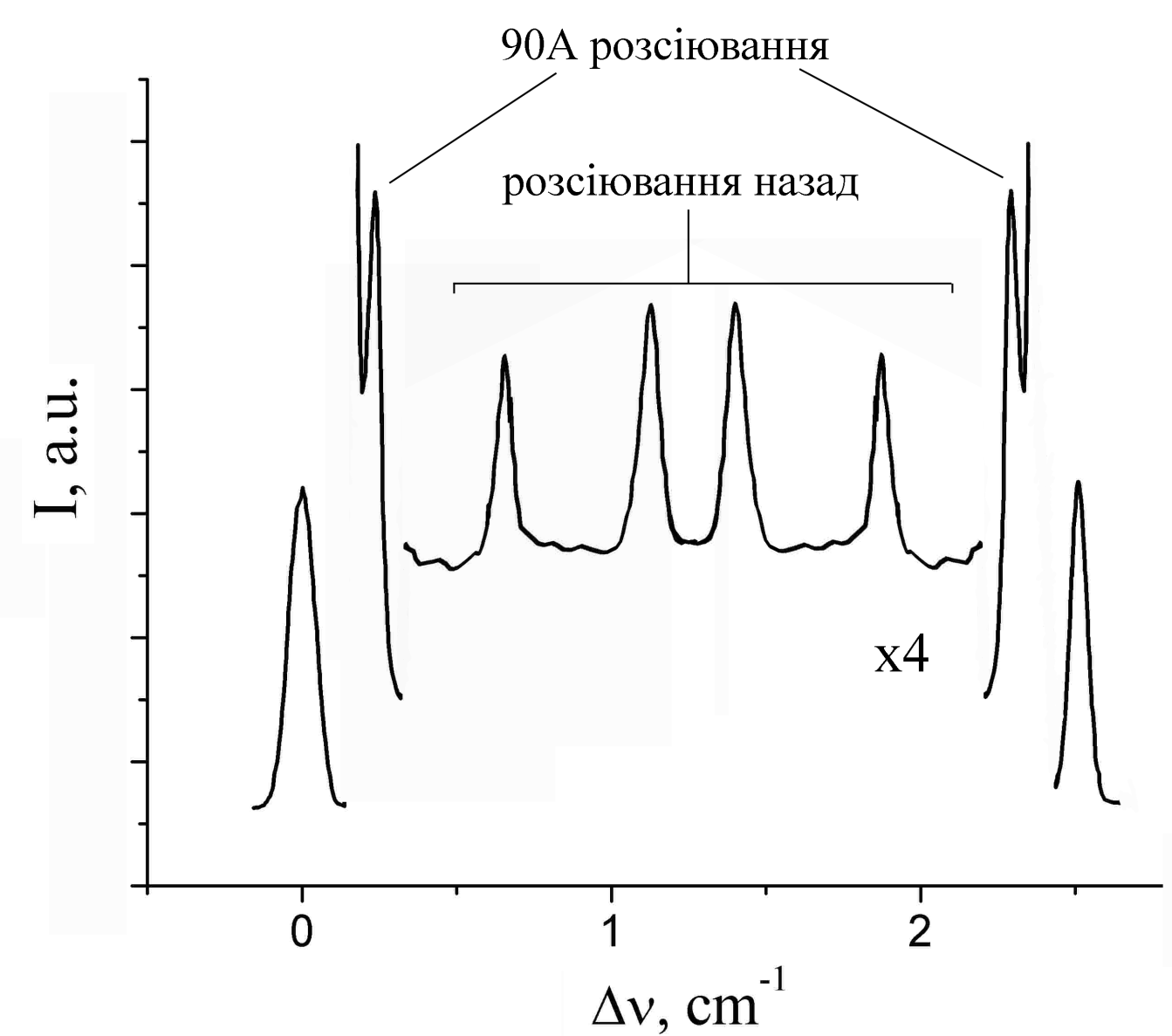
Рис. 3.4 Спектр МБР кристалу (Pb_.0.2Sn_0.8)₂P₂S₆ для êê[010], при кімнатній температурі, геометрія розсіювання 90А.

3.3. Акустичні властивості (Pb_уSn_1-y)₂P₂S₆

Всі досліджувані зразки були хорошої оптичної якості. Вони мали форму паралелепіпедів розміром близько 5х5х5 мм. Кристали типу (Pb_уSn_1‑y)₂P₂S₆ належать до моноклінної сингонії. Для них було використано так звану псевдо ромбоедричну установку з моноклінним кутом β = 91.15°.

На рис.с 3.514 зображено спектри МБР твердих розчинів (Pb_ySn_1-y)₂P₂S₆, отримані в 90⁰ геометрії розсіювання світла при кімнатній температурі з хвильовим вектором q|| Z(X0)Y. Тут чітко спостерігаються дві поперечні компоненти МБР.

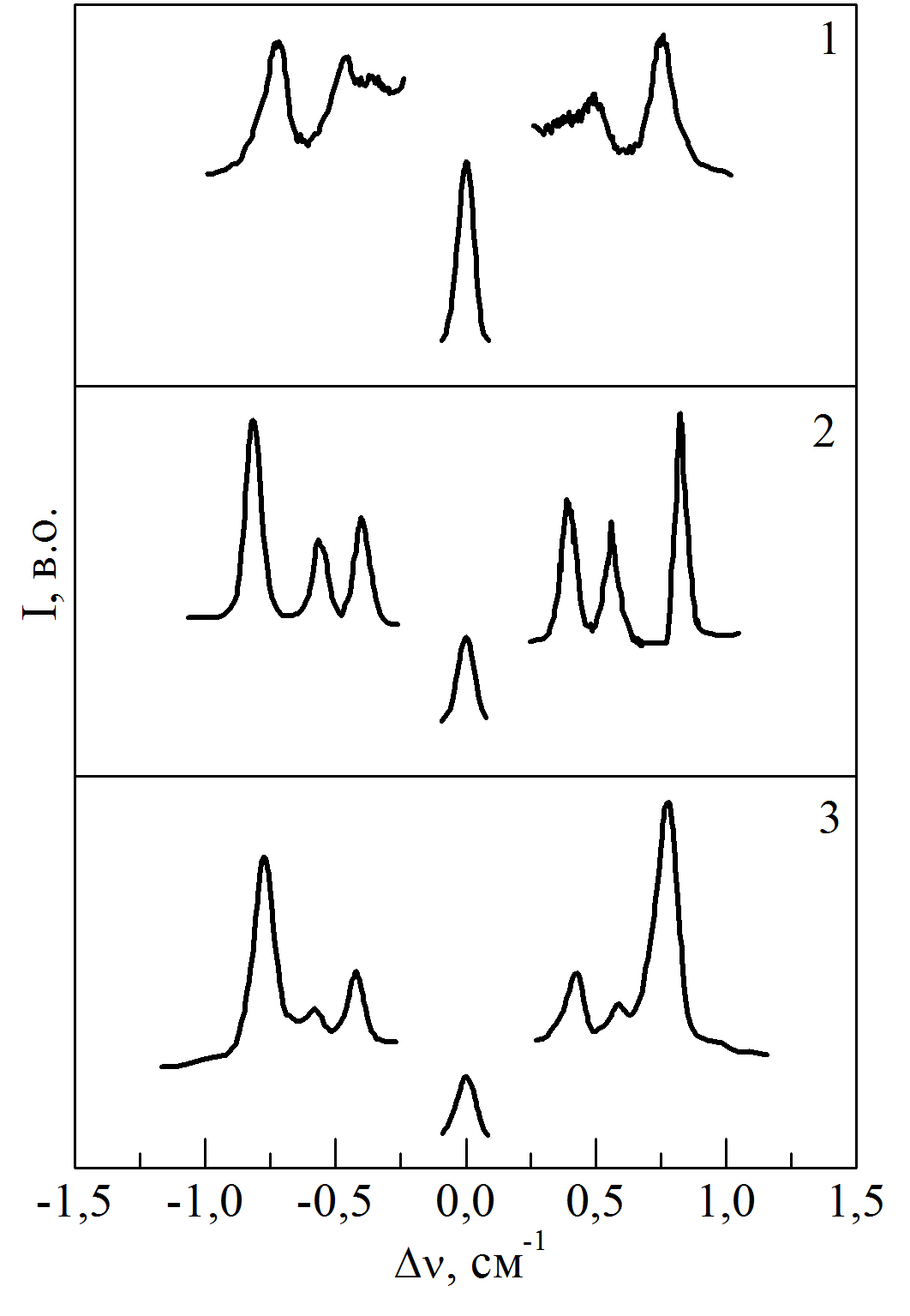
Рис. 3.514. Спектри МБР твердих розчинів(Pb_уSn_1-y)₂P₂S₆, отримані з 90⁰ геометрії розсіювання світла при кімнатній температурі для поширенняакустичної хвилі в напрямку q || Z(X 0)Y: 1 –Pb₂P₂S₆, 2 – (Sn_0.55Pb_0.45)₂P₂S₆, 3 – (Sn_0.90Pb_0.10)₂P₂S₆.

На рис. На рис. 3.615 приведений спектр МБР кристалу (Sn_0.90Pb_0.10)₂P₂S₆, отриманий при кімнатній температурі з q || z у 90A геометрії розсіювання. В цьому випадку зміщення компонент від центрального піку досить мале, тому поперечні фонони важкоспостерігати.

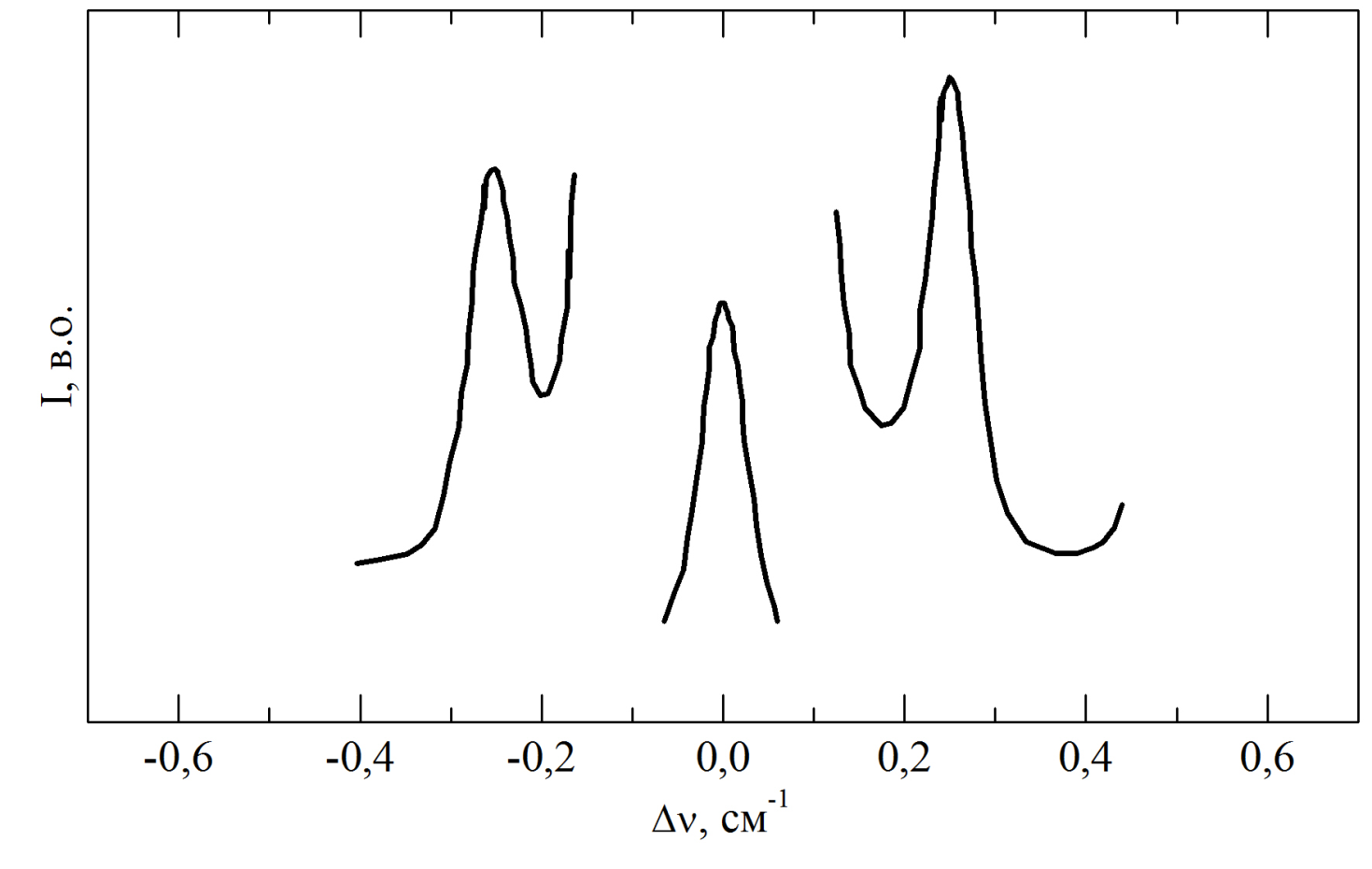
Рис. 3.615. Спектр МБР кристаллу Спектр МБР кристалу (Sn_0.90Pb_0.10)₂P₂S₆,отриманий при кімнатній температурі з q || z у 90A геометрії розсіювання.

В таблиці 3.12 представлені швидкості поширення хвиль гіперзвукового діапазону в твердих розчинах (Pb_ySn_y-1)₂P₂S₆ при кімнатній температурі вздовж різних кристалографічних напрямків, отриманих з 180⁰ і 90⁰ геометрій розсіювання, відповідно. Аналізуючи отримані результати, бачимо, що досліджувані сегнетоелектрики є істотно анізотропними.

Табл. 3.12. Швидкості поширення гіперзвуку в твердих розчинах (Pb_ySn_y‑1)₂P₂S₆ при кімнатній температурі вздовж різних кристалографічних напрямків, отримані з 90⁰ і 180⁰ геометрій розсіювання.

Напрямок	(Pb0.10Sn0.90)2P2S6 υLA, υTA1, υTA2 10^3м/с	(Pb0.20Sn0.80)2P2S6 υLA, υTA1, υTA2 10^3м/с	(Pb0.30Sn0.70)2P2S6 υLA, υTA1, υTA2 10^3м/с	(Pb0.45Sn0.55)2P2S6 υLA, υTA1, υTA2 10^3м/с	Pb2P2S6 υLA, υTA1, υTA2 10^3м/с
-Y(X 0)Z   Y(X 0)Z   -X(Y 0)Z   X(Y 0)Z   -X(Z 0)Y   X(Z 0)Y   X(Y 0)-X   X(Z 0)-X   Y(X 0)-Y   Y(Z 0)-Y   Z(X 0)-Z   Z(Y 0)-Z	3.47, 2.60, 1.88   3.46, 2.60, 1.90   3.73, 2.31, 1.73   3.71, 2.28, 1.73   3.92, 2.35, 1.62   3.91, 2.26, 1.60   3.19, 2.28, -   3.37, 2.36, -   3.16, 2.56, -   3.07, 2.61, -   3.48, -, -   3.32, -, -	3.73, 2.60, 1.84   3.69, 2.57, 1.83   3.65, 2.21, 1.68   3.70, 2.30, 1.70   3.92, 2.30, 1.58   3.92, 2.33, 1.52   3.13, -, -   3.28, -, -   3.38, -, -   3.34, -, -   3.69, -, -   3.52, 2.37, -	3.64, 2.51, 1.80   3.56, 2.38, 1.73   3.57, 2.09, 1.63   3.56, 2.28, 1.63   3.75, 2.26, 1.47   3.74, 2.12, 1.51   3.14, -, -   3.25, -, -   3.28, -, -   3.24, -, -   3.59, 2.41, -   3.42, 2.30, -	3.50, 2.36, 1.70   3.55, 2.40, 1.69   3.55, 2.09, -   3.43, 2.16, 1.56   3.66, 2.06, 1.47   3.65, 2.10, 1.45   3.07, -, -   3.21, -, -   3.17, -, -   3.12, -, -   3.44, 2.26, -   3.26, 2.14, -	3.14, 2.05, 1.59   3.11, 2.03, 1.52   3.29, 1.86, -   3.30, 1.90, -   3.35, -, -   3.29, -, -   2.95, -, -   3.01, -, -   2.96, -, -   2.90, -, -   3.01, 2.03, -   2.93, -, -[A3]

Якщо побудувати концентраційні залежності швидкості для всіх розглядуваних напрямків, то можна чітко бачити, що її поведінка для концентрацій свинцю y = 0 (Sn₂P₂S₆) і y = 0.1 помітно відрізняється від поведінки швидкостей звуку для концентрацій y = 0.2, 0.3, 0.45, 1.

Це пояснюється тим, що при кімнатній температурі кристали тіогіподифосфату олова і (Sn_0.90Pb_0.10)₂P₂S₆ знаходяться в сегнетоелектричній фазі. У Sn₂P₂S₆ при температурі 337 К відбувається сегнетоелектричний фазовий перехід змішаного характеру – між типами зміщення і лад-безлад.

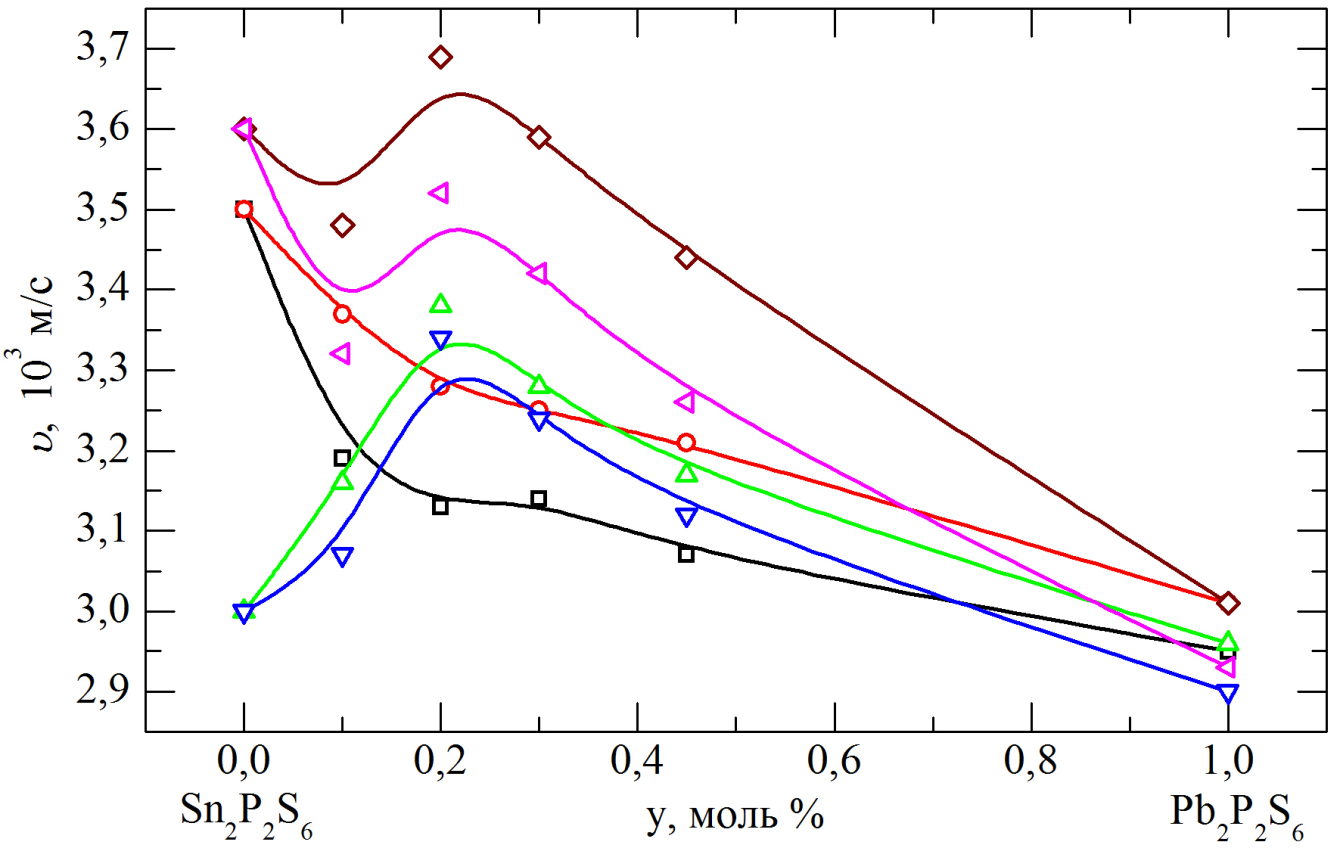[A4]

Рис. 3.716. Залежності швидкостей поширення гіперзвуку від концентрації Sn(Pb) у твердих розчинах (Pb_ySn_y-1)₂P₂S₆ при кімнатній температурі вздовж різних кристалографічних напрямків, отримані з 180° геометрії розсіювання: □ – X(Y0)-Y,○ – X(Z0)-X, – Y(X0)-Y, – Y(Z0)-Y,

◊ – Z(X0)-Z, – Z(Y0)-Z.

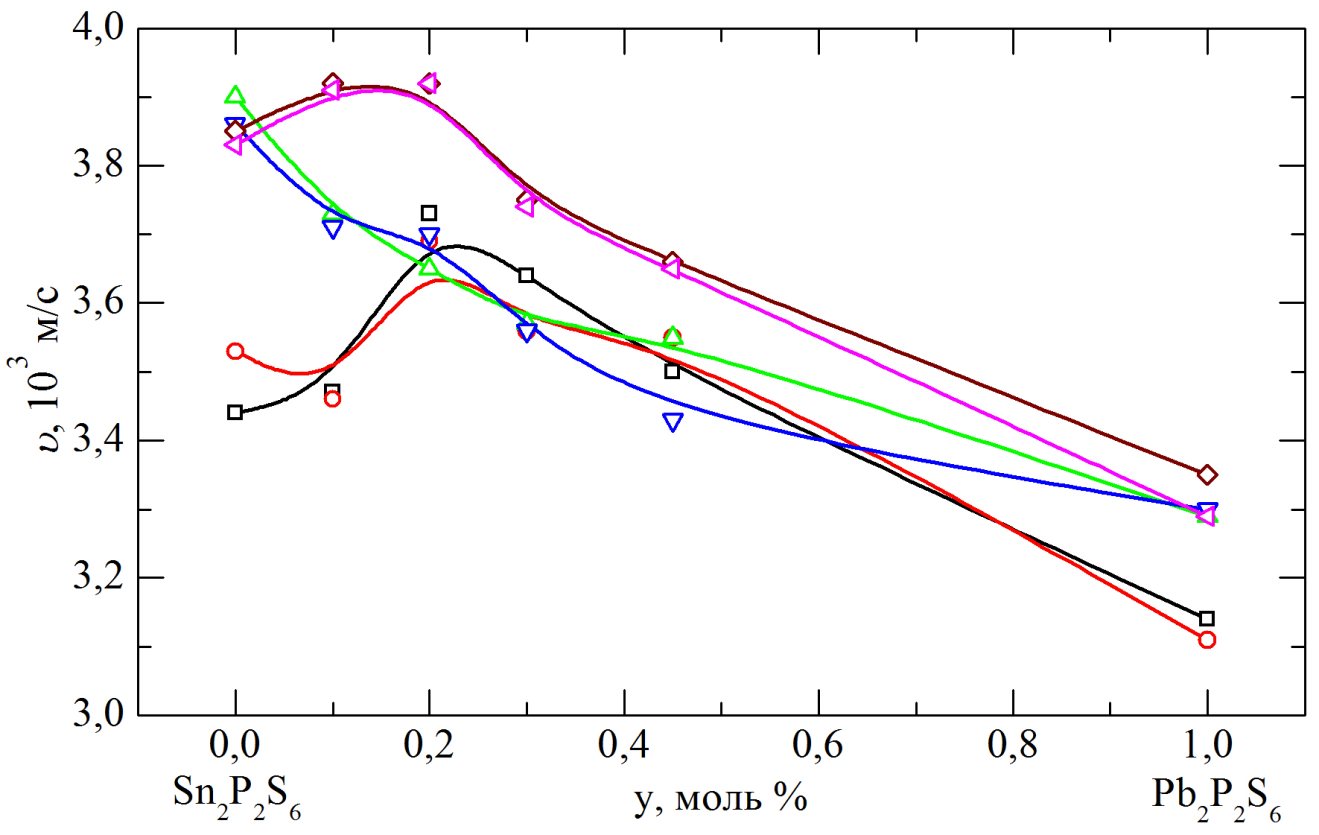[A5]

Рис. 3.817. Залежності швидкостей поширення гіперзвуку від концентрації Sn(Pb) у твердих розчинах (Pb_ySn_y-1)₂P₂S₆ при кімнатній температурі вздовж різних кристалографічних напрямків, отримані з 90° геометрії розсіювання: □ – X(Y0)-Y, ○ – Y(X0)Z, – X(Y0)Z, – X(Y0)Z,

◊ – -X(Z0)Z, – X(Z0)Y.

При переході із параелектричної фази в сегнетоелектричну швидкість поздовжньої гіперзвукової хвилі стрибком зменшується. Далі, зі зменшенням температури швидкість монотонно зростає і виходить на насичення. Для монокристалів Sn₂P₂S₆ різниця швидкостей між їх пара фазним значенням (υ_p ≈ 3440 м/с) і значенням при кімнатній температурі становить в напрямку [010] приблизно D ≈ 440 м/с, для [001] – D ≈ 268 м/с. А в напрямку [100] значення швидкості при Т_к більше ніж в парафазі. Це пов’язано з тим, що для Sn₂P₂S₆ близько до напрямку [100] орієнтований вектор спонтанної поляризації, із-за чого при поширенні пружної хвилі створюється нерівноважний розподіл поляризації. В кристалі (Sn_0.90Pb_0.10)₂P₂S₆ ситуація подібна. Для напрямку [001] –

D ≈ 266 м/с. Починаючи від вмісту свинцю y = 0.2 і зі збільшенням його концентрації до Pb₂P₂S₆, величина швидкості гіперзвукової хвилі при кімнатній температурі монотонно зменшується для всіх напрямків. В таблиці 3.23 зведені величини затухання поздовжнього гіперзвуку для досліджуваних твердих розчинів. А на рис. 3.918 зображена їх концентраційна залежність.

Табл. 3.2.3 Затухання повздовжнього гіперзвуку в твердих розчинах (Pb_ySn_y-1)₂P₂S₆ при кімнатній температурі вздовж різних кристалографічних напрямків, отримане 180⁰ геометрій розсіювання.

Напрямок	у = 0.10 α LA, 10^6м^-1	у = 0.20 α LA, 10^6м^-1	у = 0.30 α LA, 10^6м^-1	у = 0.45 α LA, 10^6м^-1	у = 1.0 α LA, 10^6м^-1
X(Y 0)-X   X(Z 0)-X   Y(X 0)-Y   Y(Z 0)-Y   Z(X 0)-Z   Z(Y 0)-Z	2.08   1.71   2.35   2.52   2.91   2.46	2.63   1.94   1.62   1.90   1.88   1.52	2.35   1.89   2.07   2.22   1.85   2.10	2.16   2.15   1.90   2.06   2.06   1.95	3.22   2.21   3.20   2.66   3.63   2.54[A6]

[A7]

Рис. 3.918. Залежності затухання повздовжнього гіперзвуку від зміни концентрації Sn(Pb) у твердих розчинах (Pb_ySn_y-1)₂P₂S₆ при кімнатній температурі вздовж різних кристалографічних напрямків, отримані з 180° геометрії розсіювання: □ – X(Y0)-Y, ○ – X(Z0)-X, – Y(X0)-Y,

– -Y(Z0)-Y, ◊ – Z(X0)-Z, – Z(Y0)-Z.

З допомогою 90А геометрії розсіювання ми отримали орієнтаційні залежності для твердих розчинів з концентраціями свинцю y = 0.1, 0.2, 0.3. Вони зображені на рис. 3.1019. Одержані результати свідчать про те, що найбільша різниця у швидкостях поздовжніх гіперзвукових фононів, що поширюються в площині (001) (див. рис. 3.1019) при кімнатній температурі притаманна для складу (Sn_0.90Pb_0.10)₂P₂S₆. Тут швидкості варіюють у межах від 2811 м/с до 3944 м/с. Для (Sn_0.80Pb_0.20)₂P₂S₆ варіація швидкостей – від 3227 м/с до 3947 м/с, і для (Sn_0.70Pb_0.30)₂P₂S₆ – від 3296 м/с до 3989 м/с. Така особливість даних орієнтаційних залежностей є також наслідком того, що твердий розчин з концентрацією свинцю y = 0.1 при кімнатній температурі знаходиться в сегентоелектричній фазі і є уже близьким до точки фазового переходу, а тверді розчини з y = 0.2 і y = 0.3 – в параелектричній фазі.

Рис.3.1019. Швидкості поздовжніх гіперзвукових хвиль, що поширюються в площині (001) для твердих розчинів (Pb_ySn_y-1)₂P₂S₆, отримані в 90А геометрії розсіювання.

3.4. Анізотропія пружних властивостей (Pb_ySn_y-1)₂P₂S₆

Розраховані орієнтаційні залежності швидкості поширення поздовжніх і поперечних гіперзвукових хвиль для твердого розчину (Pb_ySn_y-1)₂P₂S₆ показані на рис. 3.119 – 3.142. Для їх визначення з МБР визначалися швидкості гіперзвуку для різних напрямків поширення хвиль з використанням 90^о, 180^о та 90А геометрії розсіювання. Потім всі незалежні компоненти тензора пружності оцінювалися шляхом розв'язування рівняння Крістоффеля (3.12) Слід зазначити, що число незалежних компонент тензора пружності скорочено з 21 до 13 через моноклінну симетрію досліджуваних сполук. За допомогою рішення зворотного завдання рівняння Крістоффеля можна знайти значення швидкостей звуку для будь-якого напрямку поширення звукової хвилі. Для цього потрібно розв’язати кубічне рівняння (3.17) із коефіцієнтами (3.18):

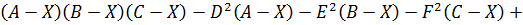
(3.17)

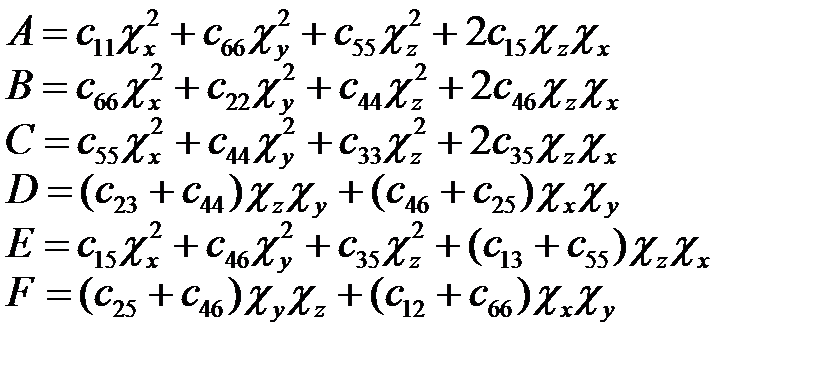, (3.18)

де 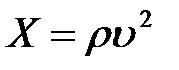, а 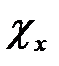, , 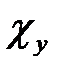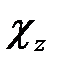– направляючі косинуси. З отриманих швидкостей гіперзвуку визначені всі 13 незалежних ненульових компонент тензора пружних модулів 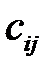для досліджуваних складів твердих розчинів (Pb_уSn_1-y)₂P₂S₆, які представлені в табл. 3.31. Поведінка відповідних коефіцієнтів 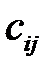при кімнатній температурі зі зміною концентрації свинцю пов’язана з концентраційними залежностями сталих ґратки досліджуваних об’єктів, а також з тим, що внаслідок збільшення вмісту свинцю при постійній температурі на фазовій діаграмі відбувається переміщення із області сегнетоелектричної фази (y ≤ 0.10) до параелектричної (y > 0.10).

Табл. 3.31. Компоненти c_ij тензора жорсткості кристалів (Pb_ySn_1-у)₂P₂S₆ при кімнатній температурі.

c × 10^-10, Н/м^2	c11	c22	c33	c44	c55	c66	c12	c13	c15	c23	c25	c35	c46
Sn2P2S6	4.2	3.2	4,5	1.6	2.2	2.2	2.0	1.8	-0.7	1.0	-0.4	0.5	0.1
(Pb0.10Sn0.90)2P2S6	4.5	3.0	4.2	1.8	2.1	2.3	1.7	2.1	0.0	0.7	-0.5	0.3	-0.1
(Pb0.20Sn0.80)2P2S6	4.7	4.7	4.9	1.5	1.9	2.2	2.0	2.6	-0.2		-1.7	0.1	-0.1
(Pb0.30Sn0.70)2P2S6	4.9	4.9	4.8	1.5	2.1	1.5	2.9	1.4	-0.1	0.9	-1.2	0.5	-0.5
(Pb0.45Sn0.55)2P2S6	4.0	4.0	4.9	1.7	2.1	2.1	2.3	2.4	-0.7	1.8	-0.8	0.2	-0.2
Pb2P2S6	4.4	4.1	4.1	1.5	2.0	1.7	2.6	2.1	0.0	2.0	0.2	0.3	-0.1

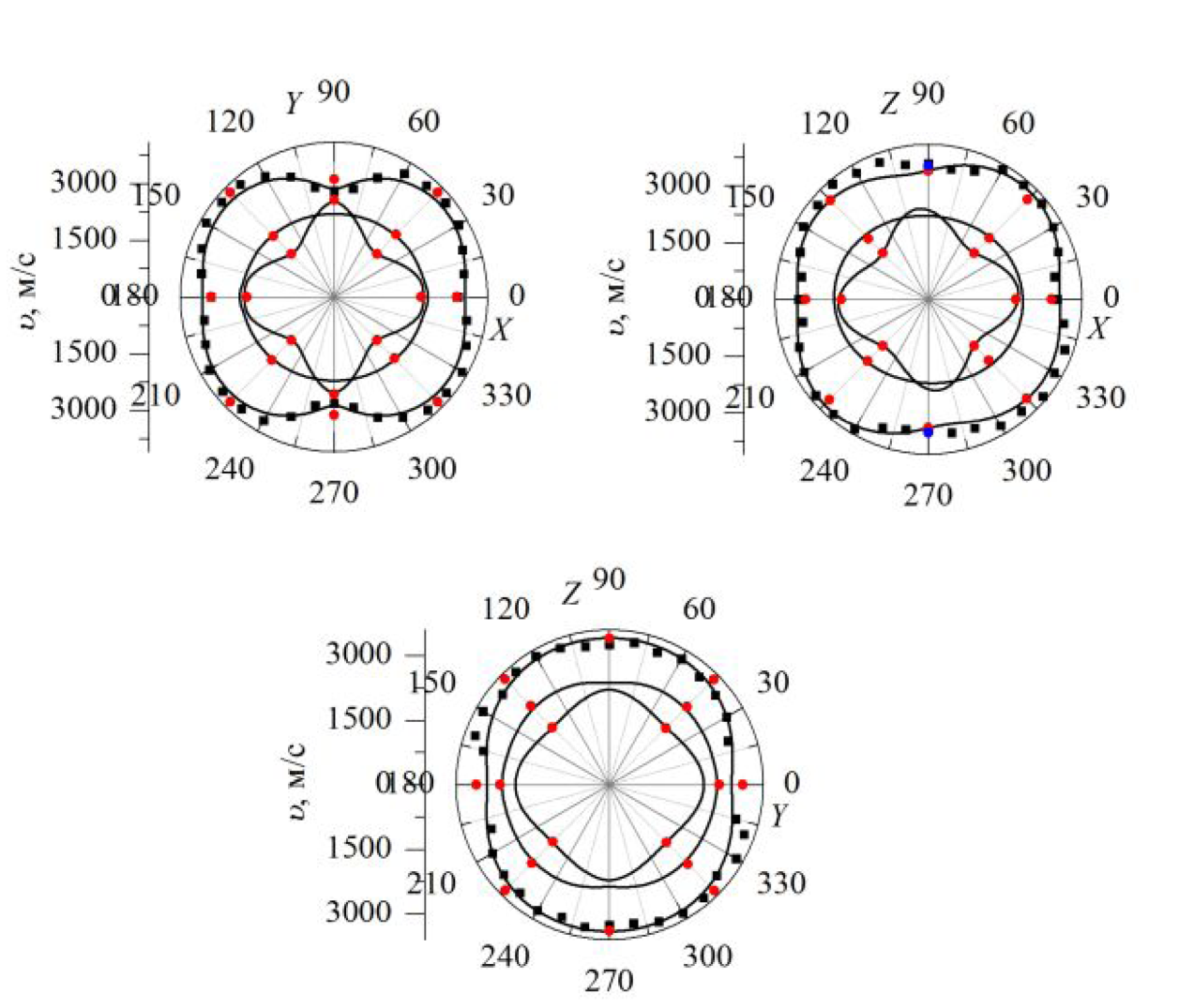
Рис. 3.119. Розрахункові індикатриси (–) та експерементально отримані значення швидкостей звуку (з 90А (■), 90⁰ та 180⁰ (●) геометрії МБР, ● – ультразвук) у кристалі (Pb_0.10Sn_0.90)₂P₂S₆ при кімнатній температурі.

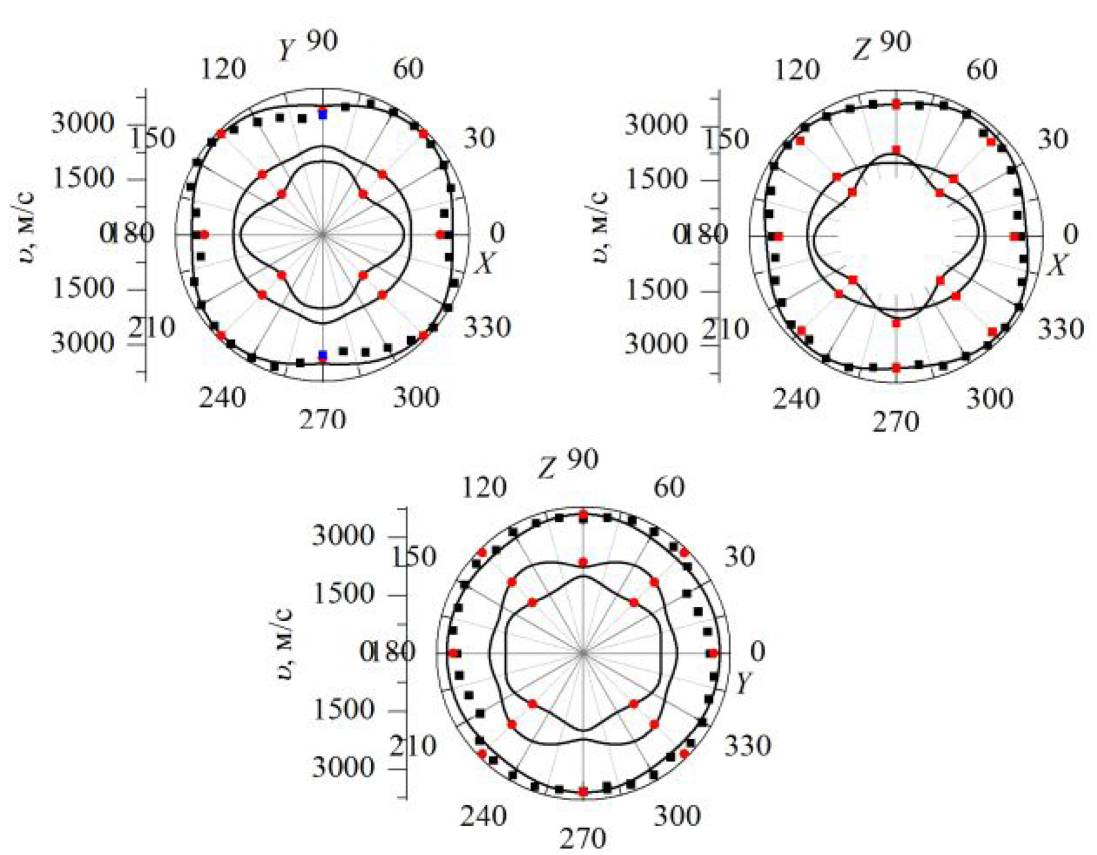
Рис. 3.1210. Розрахункові індикатриси (–) та експерементально отримані значення швидкостей звуку (з 90А (■), 90⁰ та 180⁰ (●) геометрії МБР, ● – ультразвук) у кристалі (Pb_0.20Sn_0.80)₂P₂S₆ при кімнатній температурі.

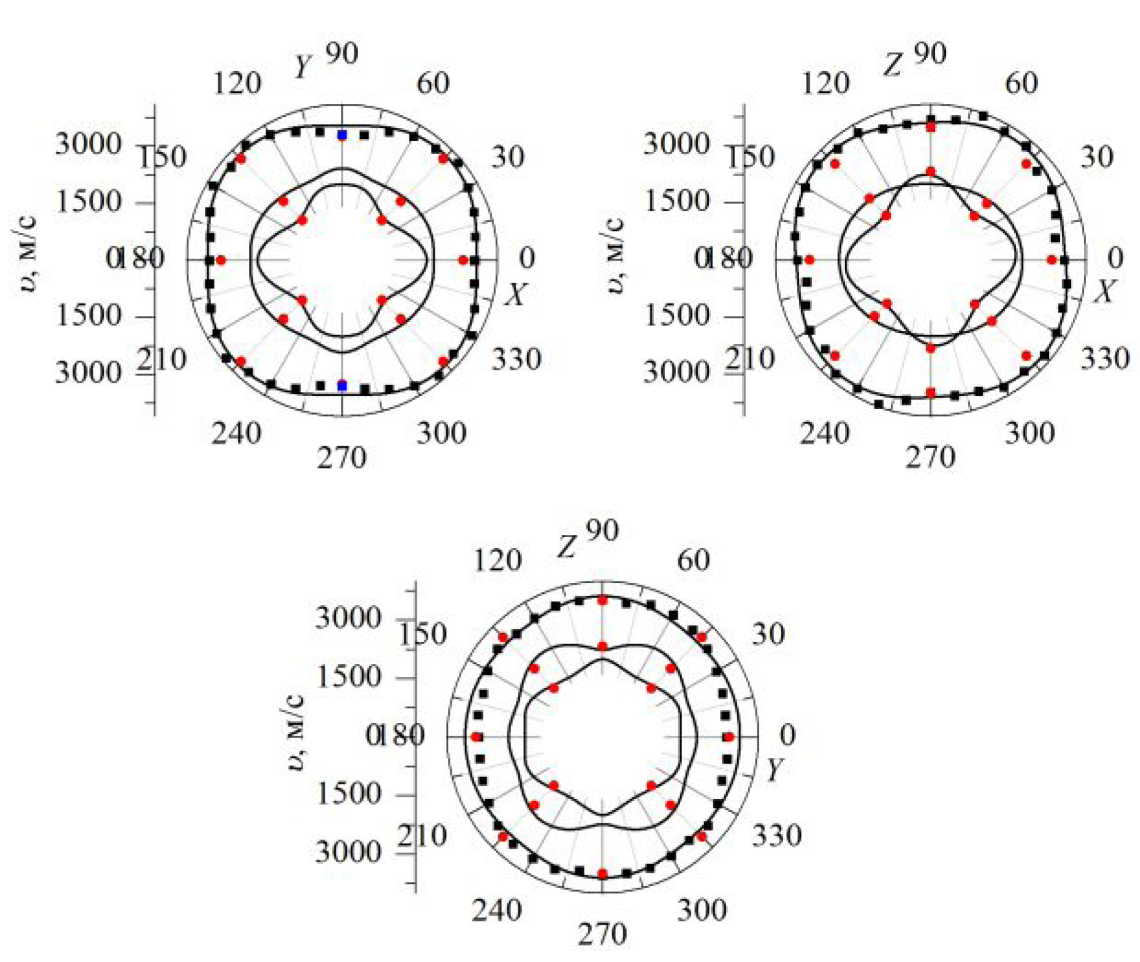
Рис. 3.131. Розрахункові індикатриси (–) та експерементально отримані значення швидкостей звуку (з 90А (■), 90⁰ та 180⁰ (●) геометрії МБР, ● – ультразвук) у кристалі (Pb_0.30Sn_0.70)₂P₂S₆ при кімнатній температурі.

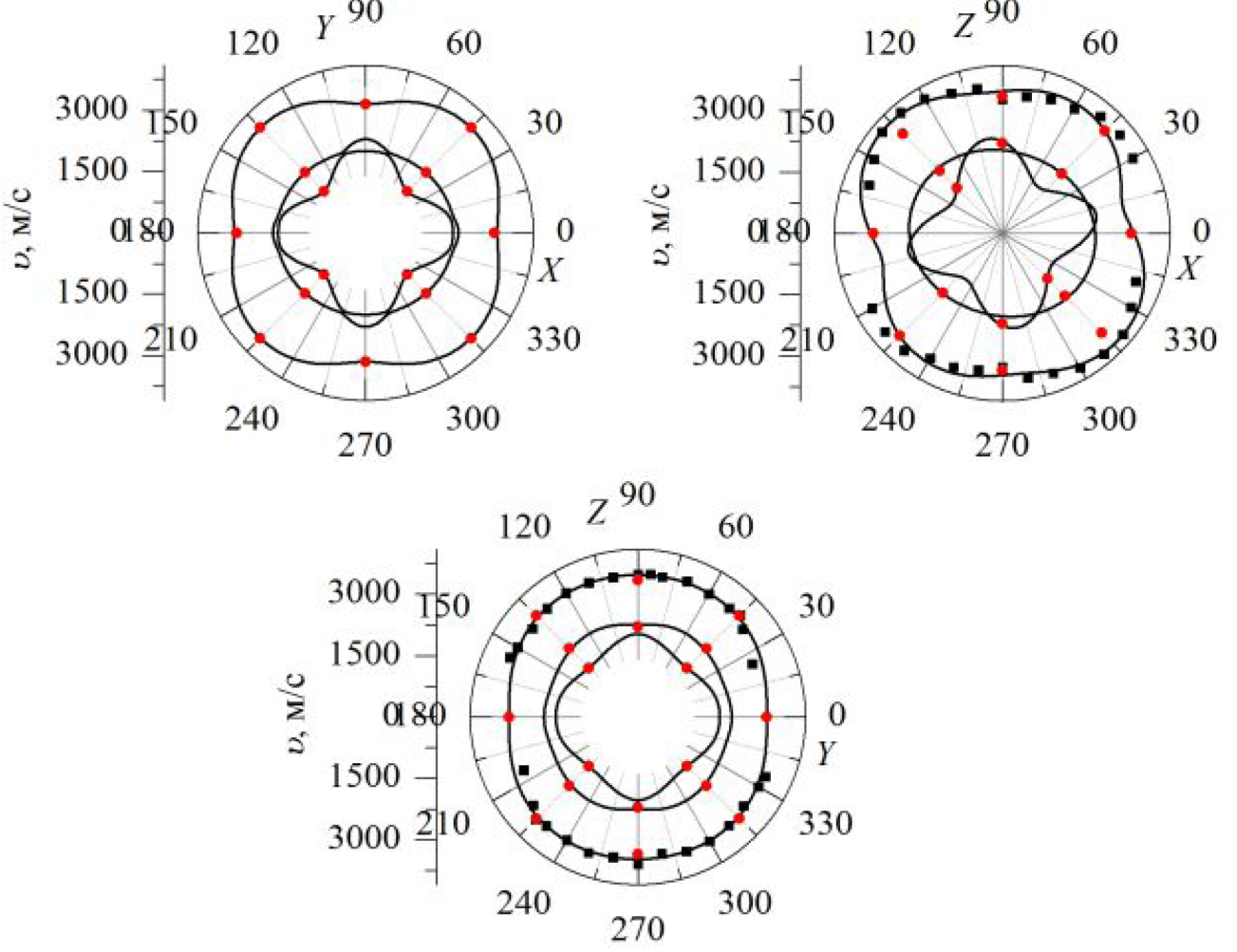
Рис. 3.142. Розрахункові індикатриси (–) та експерементально отримані значення швидкостей звуку (з 90А (■), 90⁰ та 180⁰ (●) геометрії МБР) у кристалі (Pb_0.45Sn_0.55)₂P₂S₆ при кімнатній температурі.

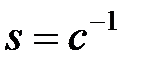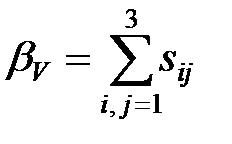Концентраційна залежність коефіцієнтів жорсткості c_ij твердих розчинів (Pb_ySn_1-у)₂P₂S₆ при кімнатній температурі зв’язана із відповідними параметрами ґратки, густиною і рухом з сегнетоелектричної фази у параелектричну на фазовій діаграмі із збільшенням концентрації іонів свинцю. Враховуючи співвідношення та , де 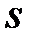– тензор податливості, 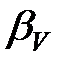– об’ємна стисливість, для досліджуваних кристалів можна знайти концентраційну залежність стисливості. Відповідні результати приведені на рис. 3.153

.

Рис. 3.153. Концентраційна залежність об’ємної стисливості кристалів (Pb_ySn_{1- у}) ₂P₂S₆ при кімнатній температурі.

Дата добавления: 2015-08-31