
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Анізотропія пружних властивостей
|
|
|
|
РОЗДІЛ 3
3.1 Пружні властивої діелектричних анізотропних кристалів
Дослідження розсіювання Мандельштама-Бріллюена в кристалах із метою вивчення їх пружних і фотопружних властивостей вийшло на перший план завдяки створенню лазерів. Результати одержуються при частотах порядка 10ГГц, що дозволяє вивчення дисперсії. Вимірювання інтенсивності спектральних ліній дозволяють розраховувати пружньооптичні константи. Проте, необхідність використання прозорих матеріалів обмежує застосування методу.
При розгляді умов поширення плоских об’ємних бігучих акустичних хвиль в діелектричних кристалах необхідно вияснити, як залежать від напрямку поширення в кристалі їх поляризація і швидкість розповсюдження. Оскільки довжини акустичних хвиль значно більші міжатомних відстаней, кристал розглядається як суцільне пружне анізотропне безмежне середовище. Опис руху малих елементів об’єму такого середовища ведеться в кристалографічній системі координат. Для кожного класу симетрії міжнародними угодами визначено розміщення елементів симетрії кристала, що належить до певного класу, в цій системі координат. Рівняння руху малого об’єму кристалу:
ρ  = ƒi =
= ƒi = 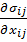 (3.1)
(3.1)
де ρ – густина, ui – компоненти вектора зміщення, ƒi – компоненти об’ємних пружних сил, що діють на даний елемент об’єму,  – компоненти тензора пружних напруг на границях цього виділеного елемента. В кожному реальному кристалі існують неоднорідні залишкові напруги. Уявімо собі рівноважний стан кристала, в якому відсутні напруги і різниця температур. Розглянемо відхилення від такого положення, пов’язане із зміщенням його елементів ui і зміною їх температури
– компоненти тензора пружних напруг на границях цього виділеного елемента. В кожному реальному кристалі існують неоднорідні залишкові напруги. Уявімо собі рівноважний стан кристала, в якому відсутні напруги і різниця температур. Розглянемо відхилення від такого положення, пов’язане із зміщенням його елементів ui і зміною їх температури  T від рівноважної температури T. Термодинаміка встановлює наступні залежності:
T від рівноважної температури T. Термодинаміка встановлює наступні залежності:
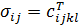 ukl - ukl -  T T
| (3.2) |
 S = S = 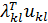 - - 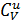  T/T T/T
| (3.3) |
Де  – компоненти тензора пружних постійних, ukl – компоненти тензора малих деформацій, СV – теплоємність,
– компоненти тензора пружних постійних, ukl – компоненти тензора малих деформацій, СV – теплоємність, 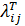 – компоненти тензора коефіцієнтів термічних напруг,
– компоненти тензора коефіцієнтів термічних напруг,  S – зміна ентропії елемента об’єму. Розповсюдження акустичних об’ємних хвиль в кристалі з великою точністю можна вважати адіабатичним аж до гіперзвукових частот. Справа в тому, що періодичні зміни температури, що пов’язані з коливаннями напруг і деформацій в акустичній хвилі, впливають лише на відстанях, значно менших довжини хвилі. При цьому зміною ентропії можна знехтувати, тоді:
S – зміна ентропії елемента об’єму. Розповсюдження акустичних об’ємних хвиль в кристалі з великою точністю можна вважати адіабатичним аж до гіперзвукових частот. Справа в тому, що періодичні зміни температури, що пов’язані з коливаннями напруг і деформацій в акустичній хвилі, впливають лише на відстанях, значно менших довжини хвилі. При цьому зміною ентропії можна знехтувати, тоді:
 T = — T = — 
| (3.4) |
Напруги при адіабатичних коливаннях:
 = = 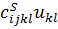
| (3.5) |
пов’язані з деформаціями адіабатичними пружними постійними. Підставляючи (3.2) в (3.1), отримаємо хвильові рівняння:
ρ  = = 
| (3.6) |
яким задовольняють розв’язки у виді бігучих плоских хвиль
ul = Apl  Apl Apl 
| (3.7) |
де А — амплітуда коливань, рі — компоненти одиничного вектора поляризації,  — циклічна частота, кр — компоненти хвильового вектора, β =
— циклічна частота, кр — компоненти хвильового вектора, β =  t — крхр. Підставляючи (3.7) в (3.6), отримаємо систему характеристичних рівнянь:
t — крхр. Підставляючи (3.7) в (3.6), отримаємо систему характеристичних рівнянь:
𝜌  = = 
| (3.8) |
де 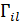 =
=  — компоненти симетричного тензора Крістофеля. Якщо помножити кожне з рівнянь системи (3.8) на
— компоненти симетричного тензора Крістофеля. Якщо помножити кожне з рівнянь системи (3.8) на  і, враховуючи, що
і, враховуючи, що  = 1 додати їх, отримаємо дисперсійне рівняння:
= 1 додати їх, отримаємо дисперсійне рівняння:

| (3.9) |
яке визначає лінійну залежність між р і  для акустичних пружних хвиль в діелектричних кристалах. Із цього слідує, що фазова швидкість пружних хвиль в даному наближенні суцільного анізотропного середовища не залежить від частоти, тобто в кристалах відсутня дисперсія фазової швидкості об’ємних хвиль. Звідси фазова швидкість розповсюдження плоскої бігучої хвилі поляризації р в напрямку
для акустичних пружних хвиль в діелектричних кристалах. Із цього слідує, що фазова швидкість пружних хвиль в даному наближенні суцільного анізотропного середовища не залежить від частоти, тобто в кристалах відсутня дисперсія фазової швидкості об’ємних хвиль. Звідси фазова швидкість розповсюдження плоскої бігучої хвилі поляризації р в напрямку 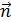 визначається з (3.9):
визначається з (3.9):

| (3.10) |
Проте, перш ніж користуватися цим виразом для розрахунків, треба вияснити, які види поляризації пружних хвиль можуть поширюватися в кристалі в напрямку 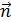 . Система рівнянь (3.8), при заданому напрямку
. Система рівнянь (3.8), при заданому напрямку 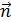 і відомих
і відомих  кристала, являється системою рівнянь для визначення компонент вектора поляризації. Використовуючи символ Кронекера, її можна представити у виді
кристала, являється системою рівнянь для визначення компонент вектора поляризації. Використовуючи символ Кронекера, її можна представити у виді
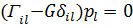
| (3.11) |
де G = ρV2 — являється власним значенням, а вектор  — власним вектором тензора Крістофеля. Умовою нетривіального розв’язку системи (3.11) являється рівність нулю її детермінанта:
— власним вектором тензора Крістофеля. Умовою нетривіального розв’язку системи (3.11) являється рівність нулю її детермінанта:
det|  | = 0 | = 0
| (3.12) |
Він має три корні  , які в загальному випадку різні. Оскільки
, які в загальному випадку різні. Оскільки  є симетричний тензор з дійсними компонентами, то його власні значення також дійсні, а відповідні їм власні вектори поляризації взаємно ортогональні. Таким чином, в загальному випадку в заданому напрямку
є симетричний тензор з дійсними компонентами, то його власні значення також дійсні, а відповідні їм власні вектори поляризації взаємно ортогональні. Таким чином, в загальному випадку в заданому напрямку 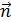 в кристалі можуть розповсюджуватися три плоскі лінійно-поляризовані пружні хвилі з взаємно-ортогональними поляризаціями, що мають різні швидкості.
в кристалі можуть розповсюджуватися три плоскі лінійно-поляризовані пружні хвилі з взаємно-ортогональними поляризаціями, що мають різні швидкості.
|
|
|
|
|
Дата добавления: 2015-08-31; Просмотров: 323; Нарушение авторских прав?; Мы поможем в написании вашей работы!