Расчет рам на устойчивость методом перемещений

III. УСТОЙЧИВОСТЬ РАМ И БАЛОК

Как было отмечено ранее, метод перемещений является универсальным методом расчета на устойчивость. При этом вводится ряд дополнительных допущений, например, не учитывается сближение концов стержней при их изгибе, а продольные деформации считаются равными нулю.

Ход расчета на устойчивость методом перемещений тот же, что и при расчете на прочность.

Устанавливается степень кинематической неопределимости системы и формируется основная система путем введения дополнительных связей, препятствующих возможным угловым и линейным смещениям узлов заданной системы.

Записывается система канонических уравнений, физический смысл которых остаётся обычным. Отличие в том, что основные неизвестные 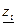являются малыми смещениями узлов, возникающими при потере устойчивости. Поскольку на раму действует узловая нагрузка, то в нагруженных элементах возникают лишь продольные усилия, а реактивные усилия в дополнительно введённых связях от внешней нагрузки 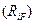до момента потери устойчивости равны нулю. Канонические уравнения метода перемещений превращаются в однородные линейные уравнения вида:

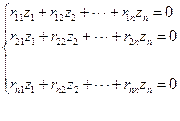
Поскольку при решении задач устойчивости рассматривается деформированное состояние системы, которую мы доводим до потери устойчивости, то неизвестные 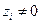. Следовательно, уравнения будут удовлетворяться при условии, когда определитель из коэффициентов равен нулю, т.е.

D=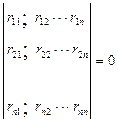

Раскрывая определитель, получаем уравнение устойчивости метода перемещений в развернутом виде.

При nk=1 уравнение устойчивости:

r11 =0

При n_k=2

Для определения реактивных усилий r_ik наложенным связям даются смещения 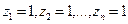и строятся эпюры 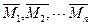. При этом для стержней, не несущих сжимающих нагрузок, можно пользоваться обычными таблицами метода перемещений, приведенными в основном курсе строительной механики. Эпюры моментов на сжатых стержнях имеют криволинейное очертание, а их ординаты содержат в виде множителей функции параметра v критической силы. Всего имеется шесть таких функци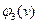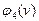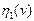й:

, , , , и .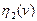

Например, 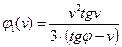; и т.д.

Параметр v и его шесть функций вводится в расчет для того, чтобы уравнения устойчивости в численном виде имели более лаконичный вид. Все функци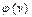и и табулированы при различных значениях v (от 0 до 2π) и приведены в любой литературе по устойчивости.

В зависимости от конкретной задачи уравнение устойчивости решается однозначно или путём пробных попыток относительно параметров v_i для загруженных стержней. Целесообразно все параметры v_i выразить через один параметр v и упростить исходные уравнения. После определения параметра v определяют критическую силу по формуле Эйлера .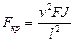

Таблица изгибающих моментов и реакций опор в сжатых стержнях от единичных перемещений

Дата добавления: 2015-08-31