
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Без учета сил сопротивления
|
|
|
|
Вынужденные колебания систем с одной степенью свободы

Этот вид колебаний рассмотрим на примере балки, где динамическая нагрузка представлена в виде гармонической, изменяющейся по синусоидальному закону,
т.е.  , где
, где 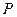 и
и  соответственно максимальная составляющая (амплитуда) нагрузки и круговая частота возмущающей силы.
соответственно максимальная составляющая (амплитуда) нагрузки и круговая частота возмущающей силы.
Уравнение динамического равновесия
 ;
; 
или, сохраняя предыдущие обозначения,

Разделив на m и обозначив  получаем неоднородное дифференциальное уравнение:
получаем неоднородное дифференциальное уравнение:

Решение уравнения в установившемся режиме имеет вид

Из решения следует, что вынужденные колебания совершаются с той же частотой, которую имеет возмущающаяся сила, а амплитуда вынужденных колебаний (yDИН) зависит от величины составляющей Р возмущающей силы P(t) и соотношения частот свободных и вынужденных колебаний.
Динамический прогиб можно представить в виде
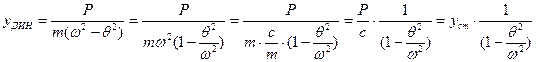
или 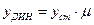 ;
; 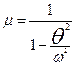
где, ycт –статический прогиб, т.е. прогиб, вызываемый статическим действием амплитудного значения динамической нагрузки P(t).
Отвлеченная величина 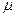 носит название динамического коэффициента и в системах с одной степенью свободы выражает отношение динамических величин (усилий, прогибов) к их статическим величинам.
носит название динамического коэффициента и в системах с одной степенью свободы выражает отношение динамических величин (усилий, прогибов) к их статическим величинам.
Представим график изменения численных значений динамического коэффициента 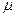 в зависимости от соотношения
в зависимости от соотношения  .
.

Из формулы для 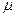 и графика видно, что с приближением частоты возмущающей силы
и графика видно, что с приближением частоты возмущающей силы  к частоте свободных колебаний
к частоте свободных колебаний  динамический коэффициент, равно как и динамический прогиб стремительно возрастают. При равенстве частот
динамический коэффициент, равно как и динамический прогиб стремительно возрастают. При равенстве частот
( =
=  ) динамический коэффициент становится равным бесконечности. Этот случай в технике носит название явления резонанса и представляет большую опасность для сооружения, так как усилия, перемещения и напряжения в элементах системы достигают больших значений. Для ответственных сооружений недопустимы не только явления резонанса, но и условия, при которых эти сооружения находились бы в зоне резонанса (см. график).
) динамический коэффициент становится равным бесконечности. Этот случай в технике носит название явления резонанса и представляет большую опасность для сооружения, так как усилия, перемещения и напряжения в элементах системы достигают больших значений. Для ответственных сооружений недопустимы не только явления резонанса, но и условия, при которых эти сооружения находились бы в зоне резонанса (см. график).
Во избежание резонанса обычно обеспечивается условие, чтобы частота свободных колебаний системы отличалась от частоты вынужденных её колебаний на 25–30 %, причем,  должна быть меньше
должна быть меньше 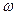 , чтобы резонанс не произошел при разгоне или остановке двигателя.
, чтобы резонанс не произошел при разгоне или остановке двигателя.
Пример:

| Определить максимальный прогиб балки и максимальный изгибающий момент.
Исходные данные возьмём из рассмотренного выше примера:
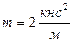 ,
EJ = 4000 кнм2, ,
EJ = 4000 кнм2,
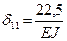 (вычислено ранее),
Pmax = 15 кн
ϴ =6,6с-1(≈ 63об/мин)
(вычислено ранее),
Pmax = 15 кн
ϴ =6,6с-1(≈ 63об/мин)
| |
Круговая частота свободных колебаний была вычислена ранее: 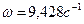 .
.
Проверяем на резонанс:
 (минимально на 25
(минимально на 25  30 %),
30 %),
в нашем случае  (30 %)(резонанс не происходит).
(30 %)(резонанс не происходит).
Динамический коэффициент равен:

Максимальный прогиб балки (на конце консоли):
 м = = 28 см
м = = 28 см
Максимальный изгибающий момент над правой опорой
 кнм
кнм
|
|
|
|
|
Дата добавления: 2015-08-31; Просмотров: 970; Нарушение авторских прав?; Мы поможем в написании вашей работы!