Понятие о степенях свободы в динамике сооружений

Задачи и методы решения задач динамики

Основными методами являются статический и энергетический.

Статический метод (точный) основан на использовании уравнений динамического равновесия, в которые дополнительно входят силы инерции перемещающихся масс. При расчёте сложных систем применение статического метода может вызвать значительные трудности ввиду громоздкости вычислений, и в этих случаях часто используются приближённые методы и способы.

В основу энергетического метода пожен закон сохранения энергии, согласно которому, при отсутствии сил сопротивления, сумма потенциальной и кинетической энергий колеблющейся упругой системы в любой момент времени остаётся постоянной.

Первая основная задача динамики сооружений заключается в исследовании так называемого спектра главных, или собственных, частот и форм колебаний упругих систем и в проверке этих систем на резонанс при действии периодических нагрузок.

Вторая основная задача динамики состоит в определении внутренних сил и перемещений, вызываемых в упругих системах динамическими нагрузками. Эту вторую задачу часто называют динамическим расчётом сооружений.

Степень свободы в динамике сооружений – это наименьшее число независимых параметров, которые определяют положения всех масс сооружения в любой момент времени при любом его движении.

Можно дать также второе определение. Степень свободы можно определять как минимальное число связей, которое нужно наложить на систему, чтобы сделать неподвижными всё её массы.

Число степеней свободы W_D является основной характеристикой системы и играет такую же роль в решении задач динамики, как, например, число лишних связей при расчёте статически неопределимых систем методом сил.

Чем большим количеством независимых перемещений обладают массы, тем сложнее её расчёт.

С целью упрощения расчёта сосредоточенные массы системы обычно считаются точечными, а также пренебрегают продольными деформации стержней при поперечных колебаниях. Вследствие этого каждая масса в балках имеет одну степень свободы.

Любая система, несущая распределённые массы, должна рассматриваться как система с бесконечной степенью свободы.

4. Свободные колебания систем с одной степенью свободы без учёта сил сопротивления

Системы с одной степенью свободы наиболее просты, но закономерности, установленные для них, справедливы и для более сложных систем.

Здесь и далее будем рассматривать только колебания без учёта сил сопротивления, т.е. незатухающие колебания с постоянной начальной амплитудой. В реальных условиях неизбежны силы сопротивления. Это – сопротивление окружающей среды (например, воздуха), трение в опорных устройствах системы, внутреннее трение частиц материала в процессе деформирования системы и др. При наличии сил сопротивления часть энергии системы необратимо расходуется на преодоления этих сил и свободные колебания затухают. Влияние сил сопротивления на колеблющуюся систему учитывается обычно в предположении, что эти силы пропорциональны скорости колебания системы.

Рассмотрим невесомую простую балку, масса которой расположена в середине пролёта. В любой момент времени перемещение у массы зависит от силы упругости S (восстанавливающая сила) и силы инерции движущейся массы J_m. Сила упругости S стремится вернуть балку на линию равновесия и при любых отклонениях массы будет направлена к линии равновесия.

Для упругих систем эта сила пропорциональна величине отклонения массы от начального положения и может быть принята равной S = c·y, где c – жесткость балки, определяемая силой, необходимой для перемещения точки расположения массы по направлению колебаний на величину, равную единице; у – отклонение массы от положения равновесия.

Сила инерции J_m выражается зависимостью:

, где – ускорение массы (знак «минус» указывает, что сила инерции направлена в сторону, противоположную ускорению).

В любой момент времени уравнение динамического равновесия () массы имеют вид S-J_m=0 или .

Разделив на m слагаемые равенства и обозначив , получаем уравнение свободных колебаний системы с одной степенью свободы без учёта сил сопротивления .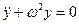

Опуская теоретические выкладки, решение этого однородного дифференциального уравнения принимает вид

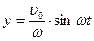
Колебания совершаются по синусоидальному закону. А – амплитуда колебаний, 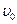– начальная скорость движения массы. Время, за которое масса совершает один полный

цикл колебаний, называют периодом колебаний Т:

Число полных циклов колебаний в единицу времени называется частотой колебания. Частоту 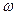, равную числу полных циклов колебаний в течение секунд, принято называть круговой частотой.

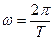или

Частота колебаний в одну секунду выражается в герцах и равна:

.

В практических расчётах часто пользуются так называемой технической частотой n (число полных циклов колебаний за одну минуту):

,

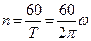Частота и период являются основными динамическими характеристиками системы. Для каждой конкретной системы они остаются постоянными величинами и зависят от упругих свойств этой системы и величины массы.

Как было отмечено выше, жёсткость с – сила, обеспечивающая перемещение, равное единице. При действии реальных нагрузок F они вызывают у_ст (статический прогиб по направлению их действия).

Вследствие этого величину с можно выразить:

Из определения жёсткости с системы также вытекает, что должно соблюдаться условие , откуда 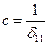, где 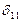– перемещение точки приложения массы по направлению колебания, вызванные силой F= 1. 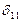можно назвать также податливостью сечения. Тогда

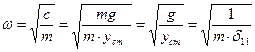, с^-1

Примеры расчёта

Пример 1

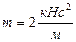
Определить круговую частоту 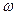и период T свободных колебаний массы.

,

(за 2π с)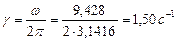

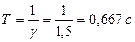
Пример 2

Определить круговую частоту .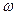

 

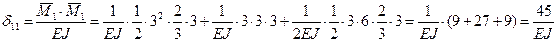
Пример 3

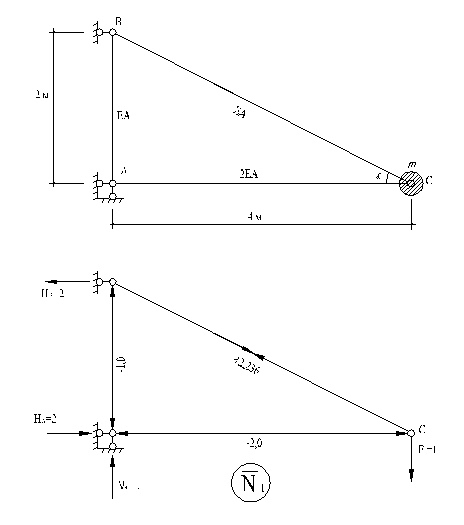
Определить частоту .

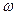Рассматриваем только поперечные колебания массы m (продольными колебаниями пренебрегаем):

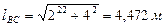
_[C^-1_]

Дата добавления: 2015-08-31