Синтез регуляторов в пространстве состояний

Рассмотрим линейную непрерывную стационарную систему в пространстве состояний:

dx / d t = Ax + Bu; y = Cx +Du.

Требуется найти управление

u = - К x,

такое, чтобы все или часть собственных чисел (мод) матрицы А - ВК замкнутой системы имели заданные значения или принадлежали заданному множеству.

Действительно, уравнение замкнутой системы

dx / d t = Ax + Bu = (А - ВК) х = Н х

и её характеристическое уравнение

det [p I - A + BK ] = 0.

Управление, основанное на применении алгебры собственных чисел передаточных матриц линейных стационарных систем, называется модальным управлением. Вектор К есть вектор постоянных коэффициентов размерностью m ´ n.

Задача синтеза заключается в определении желаемого положения корней характеристического уравнения замкнутой системы и нахождении коэффициентов К_ij, обеспечивающих заданное размещение корней.

Можно предположить, что вход системы равен нулю. Тогда и выходная величина должна быть равна нулю. На практике система подтверждена влиянию возмущений, которые стремятся сделать выход объекта отличным от нуля. Цель обратной связи по переменным состояния – вернуть значения выходной переменной и всех переменных состояния к нулю определённым, наперёд заданным, образом. Система такого типа при нулевом или постоянном входном сигнале называется регулятором состояния.

Синтез модальных систем управления основан на применении современной теории управления и называется методом размещения или назначения полюсов. Этот метод похож на метод корневого годографа, позволяющий разместить два доминирующих полюса в заданных точках. Однако современная теория позволяет реализовать заданное положение всех полюсов передаточной функции замкнутой системы. При этом возникает необходимость измерения всех или почти всех переменных состояния. Те переменные, которые не могут быть измерены непосредственно, подлежат оценке на основании измеряемых переменных. Очевидно, что такие системы используют обратную связь по состоянию и синтез регуляторов связан с понятиями управляемости и наблюдаемости.

Состоянием системы Х(t) можно управлять, изменяя вектор входа U(t), а наблюдать состояние системы можно, измеряя вектор выхода Y(t). В связи с этим возникает два вопроса:

- можно ли, выбрав соответствующим образом входы U(t), перевести объект управления из некоторого произвольного состояния X (t0) в другое состояние X (t1);

- можно ли, наблюдая вектор выхода Y(t) в течении достаточно долгого

промежутка времени, определить начальное состояние X(t0).

В большинстве систем, являющихся либо неуправляемыми, либо ненаблюдаемыми, либо то и другое, происходит сокращение нуля и полюса. Следовательно, в результате такого сокращения модель системы имеет более низкий порядок. Система, в которой число переменных состояния больше, чем её минимальный порядок, будет либо неуправляемой, либо ненаблюдаемой, либо то и другое.

Все корни характеристического уравнения можно разместить на комплексной плоскости в заданных точках только в том случае, когда система является наблюдаемой и управляемой.

Говорят, что система, описываемая матрицами (А, В) называется управляемой, если существует такое неограниченное управление u, которое может перевести систему из произвольного начального состояния x (0) в любое другое заданное состояние х (Т) за конечное время Т. Если матрица

Р =[ B AB A² B …A^n-1B]

имеет себе обратную, то система управляема.

Для системы с одним входом и одним выходом вводится понятие матрицы управляемости Р_С, которая выражается через А и В как

Р_С = [ B AB A² B …A^n-1B]

и имеет размерность n ´ n. Если определитель матрицы Р_С отличен от нуля, то система является управляемой.

Линейная стационарная система является наблюдаемой, если по значениям выходной функции y(t) можно определить начальное состояние х (0) за конечное время Т. Если матрица

Q = [ C CA CA² …CA^n-2 CA^n-1 ]^T

имеет себе обратную, то система наблюдаема.

Выбор полюсов определяется заданными показателями качества и также имеет свои ограничения. Чем больше модуль вещественной части, тем больше быстродействие системы, полоса пропускания и влияние высокочастотных помех из-за неучтённых малых постоянных времени и нелинейностей. Чем дальше полюса замкнутой системы сдвинуты по отношению к полюсам разомкнутой системы, тем большее воздействие требуется от исполнительного механизма (устройств силовой электроники, сервомеханизмов и т.д.). При этом не допускается совпадение выбранных полюсов и нулей системы управления, ибо в этом случае ухудшается управляемость системы.

Желаемое характеристическое уравнение системы можно записать в виде

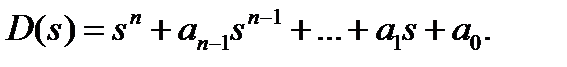
В соответствии с процедурой синтеза путём размещения полюсов необходимо найти такую матрицу К, чтобы выполнялось равенство

Это уравнение содержит n неизвестных k_i. Приравнивая в этих уравнениях коэффициенты при одинаковых степенях s, мы получим n уравнений относительно n неизвестных.

В дальнейшем ограничимся системами с одним входом и одним выходом, поэтому u(t) и y(t) есть скалярные переменные. Закон управления можно записать в виде

u(t) = - K₁x₁(t) - K₂x₂(t) - … - K_nx_n(t).

Отсюда видно, что сигнал, поступающий на вход объекта, представляет собой линейную комбинацию всех переменных состояния (рис. 69).

Рис. 69

Следовательно, и уравнения относительно неизвестных К_i будут линейными.

Пример: рассмотрим систему, дифференциальное уравнение которой в операторной форме записи имеет вид

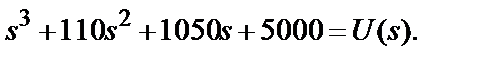
В качестве переменных состояния примем фазовые переменные, тогда уравнения состояния можно представить в матричной форме:

Матрицу обратной связи по состоянию принимаем равной

К = [ k 1 k 2 k 3].

Вычисления реализуем в MATLAB:

>> syms s k1 k2 k3 K

>> A=[0 1 0;0 0 1;-5000 -1050 -110]

A =

0 1 0

0 0 1

-5000 -1050 -110

>> B=[0;0;1]

B =

>> K=[k1 k2 k3]

K =

[ k1, k2, k3]

>> I=eye(3)

I =

1 0 0

0 1 0

0 0 1

>> D=s*I-A+B*K

D =

[ s, -1, 0]

[ 0, s, -1]

[ 5000+k1, 1050+k2, s+110+k3]

>> det(D)

ans =

s^3+110*s^2+s^2*k3+1050*s+s*k2+5000+k1

и её характеристический полином

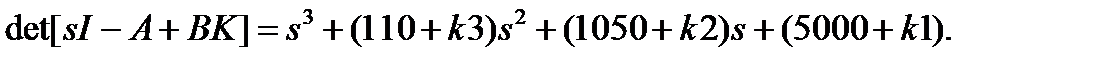
Для систем третьего порядка желательно, чтобы характеристический полином имел вид

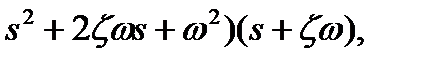
где w – собственная частота; ζ – декремент затухания. Это обеспечивает быстрое нарастание переходного процесса и малое перерегулирование, если принять z = 0,707. Потребуем также, чтобы время регулирования не превышало 0,13 с. Собственную частоту рассчитаем по выражению

t_P = 4/(zw),

откуда w = 40 c^-1. В этом случае характеристический полином имеет вид

(s² + 56,6 s + 1600) (s + 28,3) = s³ + 84,9s² + 3230s + 45280.

Приравнивая коэффициенты при одинаковых степенях s, получим

110 + k 3 = 84,9;1050 + k 2 = 3230; 5000 + k 1= 45280.

Следовательно, k 1= 40280; k 2= 2180; k 3= - 25,1.

При этих настройках время регулирования не превышает 0,13 с.

Для систем с одним входом и одним выходом матрица коэффициентов обратной связи по состоянию К = [ k ₁ k ₂ … k_n ], а управляющий сигнал u = - Kx можно определить с помощью формулы Аккермана. Если задан желаемый характеристический полином замкнутой системы

q (s) = sⁿ + a₁ s^{n- 1}+ … + a_n,

то матрица коэффициентов обратной связи по состоянию определяется выражением

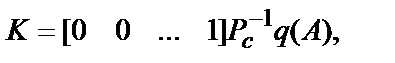
которое и называется формулой Аккермана.

Здесь

q (A)= A ⁿ + a₁ A ^{n -1}+ … + a_{n- 1} A + a_n I -

матричный полином, образованный путём использования коэффициентов желаемого характеристического уравнения q(s).

Следует отметить, что если исходная информация задана в терминах вход – выход, то Р_С – матрица наблюдаемости желаемой системы, а А – матрица состояния исходной системы.

Рассмотрим решение формулы Аккермана для предыдущего примера в MATLAB:

Расчёт матрицы управляемости желаемой системы

>> A=[0 1 0;0 0 1;-45280 -3230 -84.9]

A =

1.0e+004 *

0 0.0001 0

0 0 0.0001

-4.5280 -0.3230 -0.0085

>> B=[0;0;1]

B =

>> Pc=[B A*B A*A*B]

Pc =

1.0e+003 *

0 0 0.0010

0 0.0010 -0.0849

0.0010 -0.0849 3.9780

Расчёт обратной матрицы управляемости

>> Pci=inv(Pc)

Pci =

1.0e+003 *

3.2300 0.0849 0.0010

0.0849 0.0010 0

0.0010 0 0

Расчёт коэффициентов обратных связей

>> k=[0 0 1]

k =

0 0 1

>> Ai=[0 1 0;0 0 1;-5000 -1050 -110] – матрица состояния

Ai =

0 1 0

0 0 1

-5000 -1050 -110

>> I=eye(3)

I =

1 0 0

0 1 0

0 0 1

>> qA=Ai^3+84.9*Ai^2+3230*Ai+45280*I – матричный полином

qA =

1.0e+007 *

0.0040 0.0002 -0.0000

0.0126 0.0067 0.0005

-2.4705 -0.5063 -0.0477

>> K=k*Pci*qA

K =

1.0e+004 *

4.0280 0.2180 -0.0025 – коэффициенты обратных связей.

Это совпадает с предыдущим результатом.

Для определения матрицы К можно использовать функции K = acker(A,B,p) и К = place(A,B,p), где р – вектор-строка желаемых полюсов передаточной функции замкнутой системы управления. Первая команда может быть использована только для систем с одним входом по u при n ≤ 5. Вторая не имеет таких ограничений, однако кратность полюсов не должна превышать ранг матрицы В. Для первой команды этого ограничения нет. Ниже приведён пример использования этих функций:

>> A=[0 1 0;0 0 1;-5000 -1050 -110]

A =

0 1 0

0 0 1

-5000 -1050 -110

>> B=[0;0;1]

B =

>> p=roots([1 84.9 3230 45280])

p = -28.7821 +28.7755i

-28.7821 -28.7755i

-27.3358

>> p=[-28.78+28.78i -28.78-28.78i -27.33]

p =

-28.7800 +28.7800i -28.7800 -28.7800i -27.3300

>> K=acker(A,B,p)

K =

1.0e+004 *

4.0274 0.2180 -0.0025

>> K=place(A,B,p)

K =

1.0e+004 *

4.0274 0.2180 -0.0025

Переменные состояния характеризуют динамику системы и инженера в первую очередь интересуют такие переменные состояния, как напряжение, ток, скорость, перемещение, температура, давление и другие физические величины.

Рассмотрим математическую модель двигателя постоянного тока с независимым возбуждением (рис. 70).

Рис. 70

Принимаем за переменные состояния ток якоря i(t), угловое перемещение α (t) и ω (t). Противоэдс е = k₁Фω, электромагнитный момент М = k₂Фi, момент нагрузки М_С = k₃ω. Здесь Ф – магнитный поток, k – коэффициенты пропорциональности, J – момент инерции двигателя.

Тогда

Уравнения равновесия электрической и механической частей двигателя получены на основании закона сохранения энергии и разрешены относительно первых производных переменных состояния. Запишем эту систему в матричной форме:

или в векторно-матричной форме

dx / d t = Ax + Bu.

Рассмотрим систему тиристорный преобразователь – двигатель, представленную на рис. 71.

Рис. 71

В качестве переменных состояния выбираем угловую скорость w, ток якоря i и напряжение на выходе тиристорного преобразователя u.

Пусть К_П = 23; кФ = с = 1,36; J = 1,3; R_Я = 0,116 Ом; Т_Я = 0,06 с; Т_П = 0,01 с; Т_М = 0,0815 с; L_Я = 0, 00696 Гн; желаемый характеристический полином

q(p)= p³ + 84,9p² +3230p +45280.

Тогда уравнения в переменных состояния можно представить в виде:

dw /dt = (кФ/J) i

di /dt = (–кФ/ L_Я) w + (– R_Я / L_Я) i + (1 / L_Я) u;

du /dt = (–1/ T_П) u + (K_П / T_П) U_У;

Отсюда следует, что матрицы

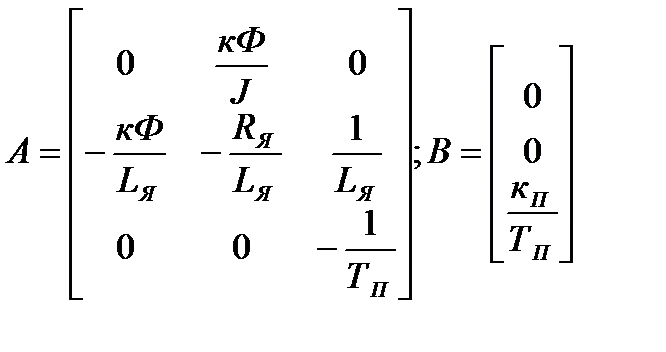
Тогда

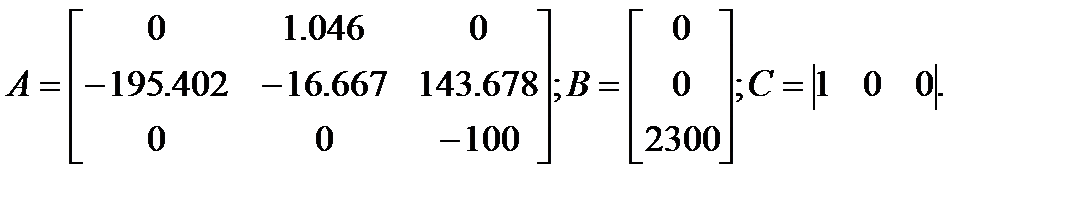
Все остальные вычисления необходимо выполнить в MATLAB.

С помощью Simulink→Continuous→State-Space создаём динамический объект, описываемый матрицами А, В, С и D. Вскрываем блок параметров и вводим эти матрицы (рис. 72). Матрицa D равна нулю. Вектор начальных условий также считаем равным нулю. Абсолютную погрешность моделирования программа выберет автоматически.

Проверяем объект на управляемость и наблюдаемость:

>> A=[0 1.046 0;-195.402 -16.667 143.678;0 0 -100]

A =

0 1.0460 0

-195.4020 -16.6670 143.6780

0 0 -100.0000

>> B=[0;0;2300]

B =

>> C=[1 0 0]

C =

1 0 0

>> Pc=[B A*B A*A*B]

Pc =

1.0e+007 *

0 0 0.0346

0 0.0330 -3.8554

0.0002 -0.0230 2.3000

>> det(Pc)

ans =

-2.6272e+014

Рис. 72

На рис. 73 представлена переходная функция – прямой пуск двигателя – изменение угловой скорости двигателя во времени.

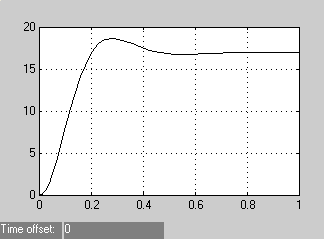
Рис. 73

Для формирования матриц управляемости и наблюдаемости предусмотрены функции Co=ctrb(A,B) и Ob=obsv(A,C):

>> Co=ctrb(A,B)

Co =

1.0e+007 *

0 0 0.0346

0 0.0330 -3.8554

0.0002 -0.0230 2.3000

>> rank(Co)

ans =

>> Ob=obsv(A,C)

Ob =

1.0000 0 0

0 1.0460 0

-204.3905 -17.4337 150.2872

>> rank(Ob)

ans =

Так как ранг этих матриц равен трём, то объект управления управляем и наблюдаем.

Далее выполняем расчет матрицы коэффициентов обратных связей:

>> Pci=inv(Pc)

Pci =

0.0048 0.0003 0.0004

0.0003 0.0000 0

0.0000 0 0

>> I=eye(3)

I =

1 0 0

0 1 0

0 0 1

>> q=A*A*A+84.9*A*A+3230*A+45280*I

q =

1.0e+005 *

0.3133 0.0198 -0.0477

-3.6899 -0.0014 7.2774

0 0 -4.2872

>> K=[0 0 1]*Pci*q

K = 0.0906 0.0057 -0.0138

Структурные схемы математической модели двигателя и системы автоматического управления с обратными связями представлены на рис. 74.

Рис. 74

Если к системе предъявляется требование астатизма как по постоянному входному сигналу, так и по нагрузке, то этого можно добиться только с помощью ПИ-регулятора (рис. 75), при этом порядок n системы увеличивается на единицу.

Рис. 75

Синтез регулятора осуществим также методом размещения полюсов. Задачу целесообразно решать при наличии единичной обратной связи по скорости. Уравнения состояния и входной сигнал объекта

dx / dt = Ax + Bu;

y = Cx = [1 0 0 0] x ₁;

u = –Kx – K ₄ x ₄;

dx ₄ /dt = x ₁ – U,

где x ₄ – выходная координата интегратора ПИ-регулятора.

Данную систему уравнений можно представить в виде

dx_f /dt = A_f x_f – B_f K_f x_f + 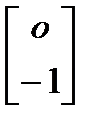U,

где

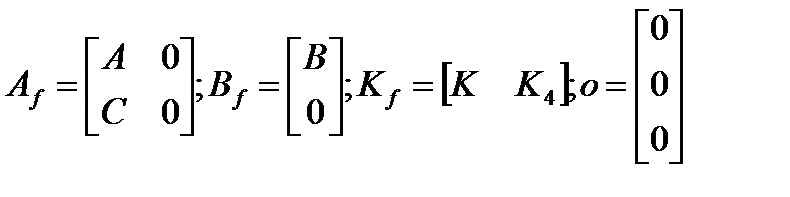
или

Характеристическое уравнение системы

.

Желаемое характеристическое уравнение зададим в виде полинома Баттерворта четвёртого порядка (время переходного процесса t _п @ 0, 12 с):

.

Матричный полином, образованный путём использования коэффициентов желаемого характеристического уравнения

Программа определения коэффициентов в MATLAB

>> Af=[0 1.046 0 0;-195.402 -16.667 143.678 0;0 0 -100 0;1 0 0 0]

Af =

0 1.0460 0 0

-195.4020 -16.6670 143.6780 0

0 0 -100.0000 0

1.0000 0 0 0

>> Bf=[0;0;2300;0]

Bf =

>> Pc=[Bf Af*Bf Af*Af*Bf Af*Af*Af*Bf]

Pc =

1.0e+009 *

0 0 0.0003 -0.0403

0 0.0003 -0.0386 3.8796

0.0000 -0.0002 0.0230 -2.3000

0 0 0 0.0003

>> det(Pc)

ans =

-9.0812e+019

>> Pci=inv(Pc)

Pci =

0.0048 0.0003 0.0004 0.0591

0.0003 0.0000 0 0.0054

0.0000 0 0 0.0003

0 0 0 0.0000

>> I=eye(4)

I =

1 0 0 0

0 1 0 0

0 0 1 0

0 0 0 1

>> q=Af^4+174*Af^3+15156*Af^2+773333*Af+19753086*I

q =

1.0e+008 *

0.1723 0.0056 0.0099 0

-1.0467 0.0830 -0.1780 0

0 0 0.1998 0

0.0074 0.0001 0.0001 0.1975

>> K=[0 0 0 1]*Pci*q

K =

2.1442 0.0373 0.0249 57.1459

Структурная схема системы управления с ПИ-регулятором представлена на рис. 76. Результаты расчётов были проверены в системе MATLAB 6.5 + Simulink 4 (рис. 77). Очевидно, что переходный процесс в системе с ПИ – регулятором (кривая 3) имеет лучшие показатели качества по сравнению с прямым пуском (кривая 1) и оптимальными связями (кривая 2).

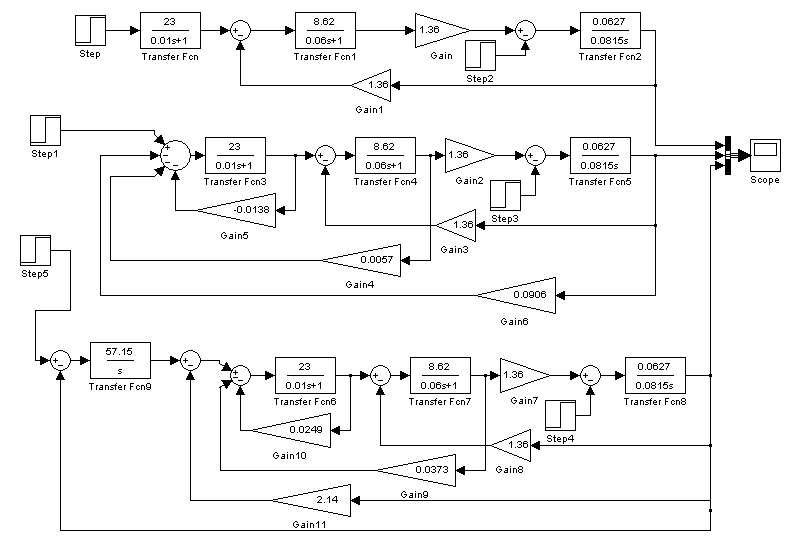
Рис. 76

Быстродействие системы возросло примерно в 2,5 раза по сравнению с прямым пуском двигателя, отсутствует перерегулирование и система лучше отрабатывает изменение нагрузки; блоки К ₂ и К ₃ являются датчиками тока и скорости, их можно рассматривать как пропорциональные регуляторы, реализующие жёсткие отрицательные обратные связи по соответствующим переменным состояния и улучшающие динамику системы в целом; блок К ₁ реализует положительную обратную связь по напряжению тиристорного преобразователя, очевидно, это компенсирует внутреннее падение напряжения преобразователя и стабилизирует напряжение питания двигателя; при выборе К_I учитывается влияние внутренней обратной связи по ЭДС; система в целом является статической, обладает заданными динамическими свойствами и может быть рекомендована для приводов, не требующих нулевой статической ошибки; система имеет более плавные переходные процессы и большее быстродействие по сравнения с стандартными настройками по критериям модульного и симметричного оптимумов.

Все примеры, приведённые выше, рассматривались при условии нулевого входного сигнала. Так как у системы нет входного воздействия (Х_З = 0), то система будет возвращать все переменные состояния к нулю после того как они по той или иной причине приняли ненулевое значение. На практике система должна отслеживать входное воздействие и управление в этом случае принимает вид

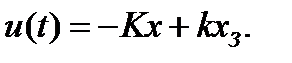
Время, с

1 – прямой пуск; 2 – с обратными связями; 3 – с ПИ – регулятором

Рис. 77

В этом уравнении неизвестным является коэффициент k и его находят, используя различные критерии синтеза. Кроме того, коэффициенты передачи датчиков обратных связей k_д не равны единице. Поскольку общий коэффициент обратной связи по переменной x_i должен быть равен k_i, то необходимо ввести дополнительный блок с коэффициентом передачи k_i/k_д. При этом необходимо изменять и масштаб входного сигнала.

Элементы матриц A, B, C могут отличаться друг от друга на несколько порядков, что создает определённые вычислительные трудности при определении матриц управляемости и наблюдаемости.В этом случае целесообразно оценить управляемость и наблюдаемость системы с помощью функций Грама, которые называются грамианами, для непрерывных в пространстве состояний систем определяются интегралами

соответственно, и более удобны для вычислений.

По определению, грамиан управляемости Gc положительно определён тогда и только тогда, когда пара матриц (А, В) является управляемой. Аналогично, грамиан наблюдаемости Go положительно определён тогда и только тогда, когда пара матриц (А, С) является наблюдаемой. В MATLAB предусмотрены две функции:

- Gc = gram(sys,’c’) – вычисляет грамиан управляемости для непрерывной или дискретной системы;

- Go = gram(sys,’o’) – вычисляет грамиан наблюдаемости для непрерывной или дискретной системы:

>> A=[0 1.046 0;-195.402 -16.667 143.678;0 0 -100]

A =

0 1.0460 0

-195.4020 -16.6670 143.6780

0 0 -100.0000

>> B=[0;0;2300]

B =

>> C=[1 0 0]

C =

1 0 0

>> D=0

D = 0

>> sys=ss(A,B,C,D)

a =

x1 x2 x3

x1 0 1.046 0

x2 -195.4 -16.67 143.7

x3 0 0 -100

b =

u1

x1 0

x2 0

x3 2300

c =

x1 x2 x3

y1 1 0 0

d =

u1

y1 0

Continuous-time model.

>> Gc=gram(sys,'c')

Gc =

1.0e+005 *

0.0172 -0.0000 0.0033

-0.0000 2.7597 0.3201

0.0033 0.3201 0.2645

>> det(Gc)

ans =

1.0783e+013

>> Go=gram(sys,'o')

Go =

0.0708 0.0026 0.0032

0.0026 0.0002 0.0002

0.0032 0.0002 0.0003

>> det(Go)

ans =

3.8607e-012

Обе матрицы положительно определены, следовательно, система управляемая и наблюдаемая.

Грамианы используются также для понижения порядка системы (построения их минимальных реализаций).

Достоверность компьютерных вычислений можно улучшить балансировкой системных матриц – их замене более пригодными для численных расчётов. Операция балансировки делает примерно равными наибольшие суммы абсолютных значений чисел каждого столбца и строки примерно равными, в MATLAB для этого используется команда [sysb,T] = ssbal(sys):

>> [sysb,T]=ssbal(sys)

a =

x1 x2 x3

x1 0 33.47 0

x2 -6.106 -16.67 17.96

x3 0 0 -100

b =

u1

x1 0

x2 0

x3 17.97

c =

x1 x2 x3

y1 32 0 0

d =

u1

y1 0

Continuous-time model.

T =

0.0313 0 0

0 0.0010 0

0 0 0.0078

Очевидно, что новая матрица а хорошо сбалансирована.

Дата добавления: 2015-08-31