Квадратичных оценок качества

Синтез регуляторов с помощью интегральных

Рассмотрим метод синтеза оптимальных систем управления с использованием обратной связи по состоянию и интегральных квадратичных оценок качества [26-29], представленных в функции вектора состояния

.

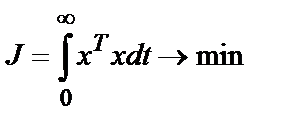Для получения минимального значения J будем считать, что существует производная

если положить, что

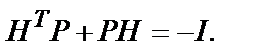
Тогда

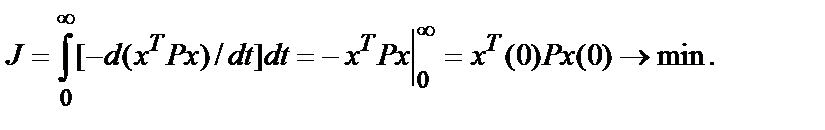
При подстановке верхнего предела интегрирования мы предполагали, что система устойчива и, следовательно, х (¥) = 0.

Таким образом, чтобы минимизировать оценку качества J, необходимо определить матрицу Р, удовлетворяющую уравнениям

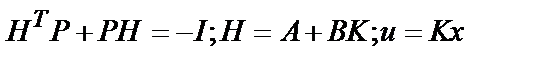
и найти минимум интегральной квадратичной оценки качества

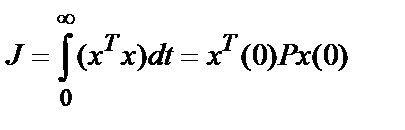
путем настройки одного или нескольких параметров системы.

Рассмотрим в качестве примера систему, у которой

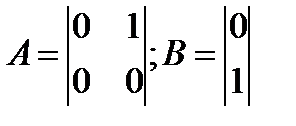
Управляющий сигнал выберем в виде линейной комбинации двух переменных состояния:

u = - к₁х – к₂х,

тогда

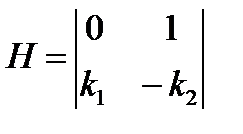
Решение матричного уравнения

H^T P + P H = - I

при условии, что матрица Р – симметричная, и k₁ = 1, приводит к следующему результату:

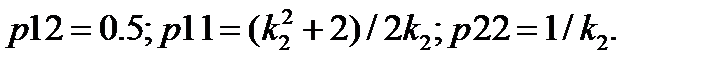
Если 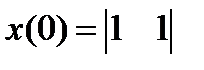, то

.

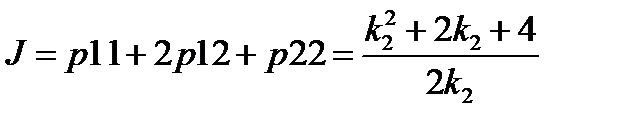Приравняем производную dJ/dk₂ нулю, отсюда k₂ = 2 и минимальное значение J = 3.

Матрица Н для скорректированной замкнутой системы примет вид:

,

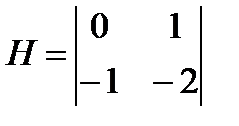характеристическое уравнение будет равно

det p I – H = p² + p2 + 1 = 0

и переходный процесс апериодический.

Чтобы учесть затраты энергии на выработку управляющего сигнала, можно использовать оценку качества

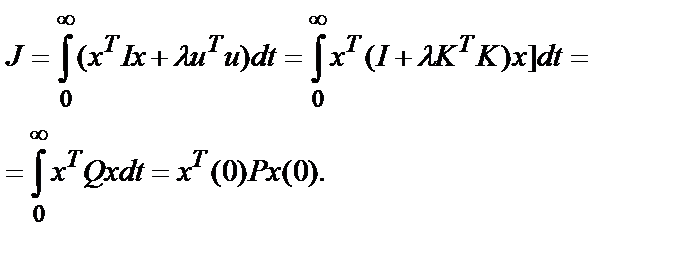
Матрица Р, как и раньше, подчиняется уравнению

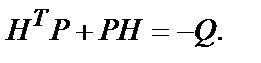
Скалярный весовой коэффициент l следует выбирать так, чтобы вклад переменных состояния в оценку качества был сопоставим с вкладом в неё второго слагаемого подинтегрального выражения, учитывающего ограниченные энергетические возможности системы.

В более сложных случаях матрица Р размерности n ´ n находится из решения уравнения Рикатти

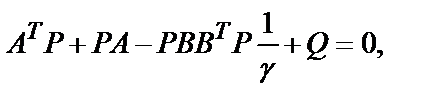
где γ – скалярный весовой коэффициент. Во многих случаях Q = I.

Другой подход к задаче стабилизации основан на том, что если система устойчива, то у неё есть квадратичная функция Ляпунова вида

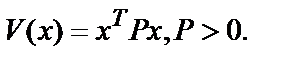(1)

Рассмотрим систему

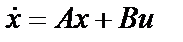
с обратной связью по состоянию 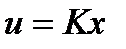и уравнением замкнутой системы

.

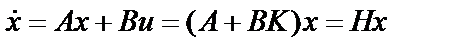Тогда, если найдутся К и Р > 0 такие, что

,

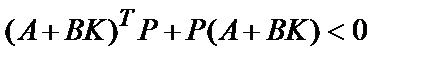то для системы существует функция Ляпунова вида (1). Две матричные переменные, Р и Q, входят в это неравенство нелинейным образом. Введением двух новых переменных – Y=KQ, Q=P ^-1 – это неравенство становится линейным по переменным Р и Q.

Матрица коэффициентов обратных связей регулятора определяется на основании следующей теоремы: если Q – решение матричного неравенства Ляпунова 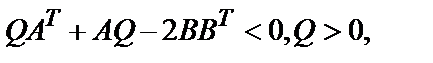то регулятор 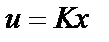с матрицей 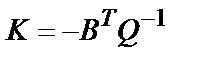стабилизирует систему 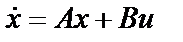, а квадратичная форма 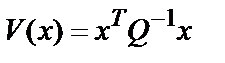является функцией Ляпунова для замкнутой системы.

Поиск квадратичной функции Ляпунова называется квадратичной стабилизацией. Он не дает решения в явном виде, а сводит задачу к решению линейных матричных неравенств. Однако такой подход особенно эффективен для задач робастной стабилизации объектов управления при наличии неопределённостей.

Дата добавления: 2015-08-31