Решение задач оптимизации в MATLAB

В MATLAB [15-20] с помощью оператора lqr(A,B,Q,R,N) реализуется проектирование линейно-квадратичного регулятора для непрерывных линейных систем. Результатом расчёта является матрица К оптимальных обратных связей по переменным состояния х, при использовании которых реализуется оптимальное управление u^* = - Kx и минимизируется функционал

,

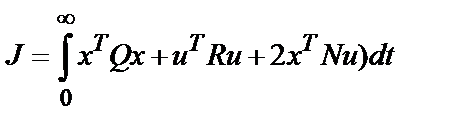если объект управления описывается векторно-матричным уравнением

.

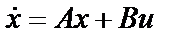Одновременно вычисляются матрица Р (в MATLAB эта матрица обозначается S) – решение уравнения Риккати

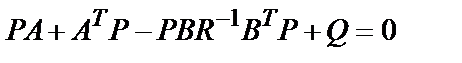
и собственные значения Е замкнутой системы управления

.

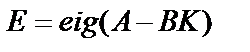Матрица N по умолчанию принимается нулевой, если при обращении к процедуре lqr(*) она не указана.

Рассмотрим применение этого оператора для синтеза системы управления двигателем постоянного тока:

>> A=[-100 0 0;143.678 -16.667 -195.402;0 1.046 0]

A =

-100.0000 0 0

143.6780 -16.6670 -195.4020

0 1.0460 0

>> B=[2300;0;0]

B =

>> C=[0 0 1]

C =

0 0 1

>> D=[0]

D =

>> R=1

R =

>> Q=eye(3)

Q =

1 0 0

0 1 0

0 0 1

>> [K,S,E]=lqr(A,B,Q,R)

K =

1.0114 0.8869 0.2545 – матрица коэффициентов обратных связей

S =

0.0004 0.0004 0.0001

0.0004 0.0066 0.0024 - решение уравнения Риккати (матрица Р),

0.0001 0.0024 1.4784 симметричная матрица

E =

1.0e+003 *

-2.2977 - корни характеристического уравнения замкнутой

-0.1434 системы управления (собственные значения

-0.0018 замкнутой системы)

>> k=R^(-1)*B'*S

k =

1.0114 0.8869 0.2545 - матрица коэффициентов обратных

связей

С помощью оператора lqry(P,Q,R,N) минимизируется функционал

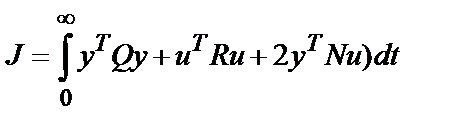
не по вектору состояния, а по вектору выхода у. Модель объекта управления Р должна быть задана в форме

,

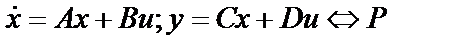и сама ss- модель является параметром процедуры:

>> Р=ss(A,B,C,D)

a =

x1 x2 x3

x1 -100 0 0

x2 143.7 -16.67 -195.4

x3 0 1.046 0

b =

u1

x1 2300

x2 0

x3 0

c =

x1 x2 x3

y1 0 0 1

d =

u1

y1 0

>> Q=1

Q =

>> [K,S,E]=lqry(p,Q,R)

K =

0.0271 0.0247 0.9058

S =

0.0000 0.0000 0.0004

0.0000 0.0000 0.0005

0.0004 0.0005 0.0307

E =

1.0e+002 *

-1.0478

-0.3708 + 0.4393i

-0.3708 - 0.4393i

На рис. 78 представлена структурная схема системы управления с оптимальными обратными связями, а на рис. 79 – переходная функция.

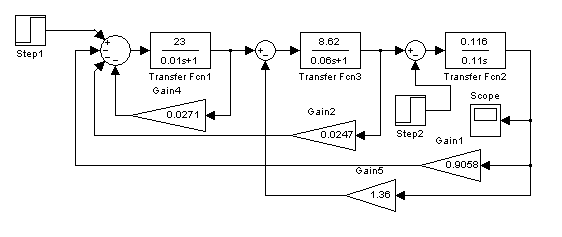
Рис. 78

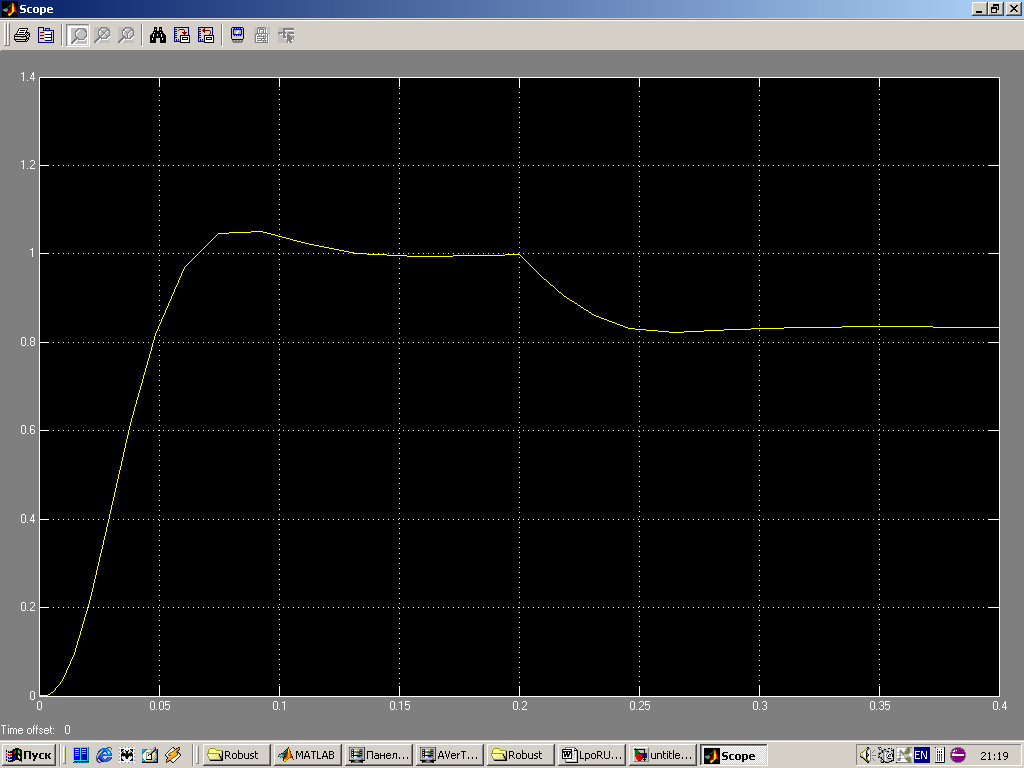
Рис. 79

Таким образом, для одной и той же системы управления существует несколько управлений, которые будут оптимальными в соответствии с выбранными критериями качества. Задачи оптимального управления могут быть решены методами вариационного исчисления, принципом максимума Понтрягина, динамическим программированием, компромиссным управлением, с помощью функций Ляпунова и уравнения Риккати, Н_∞-оптимизации.

Литература

1. IPC – CAD.

2. Ключев В.И. Теория электропривода [Текст]: Учеб. для вузов. - 2-е изд. перераб. и доп. – М.: Энергоатомиздат, 1988. – 704 с.: ил.

3. В.В. Рудаков. Электроприводы с программным управлением и последовательной коррекцией [Текст]: Учеб. пособие / Ленингр. горный ин-т. Л., 1990.

4. Егоров В.Н., Шестаков В.М. Динамика систем электропривода. [Текст] -Л.: Энергоиздат. Ленингр. отд-ние, 1983.

5. Онищенко Г.Б. Электрический привод: учебник для студ. высш. учеб. заведений/Г.Б. Онищенко. – М.: Издательский центр <<Академия>>, 2006. – 288 с.

6. Белов М.П. Автоматизированный электропривод типовых производственных механизмов и технологических комплексов: Учебник для вузов/ М.П. Белов, В.А. Новиков, Л.Н. Рассудов. – М.: Издательский центр <<Академия>>, 2004. – 576 с.

7. Терехов В.М. Системы управления электроприводом: Учебник для студ. высш. учеб. заведений/ В.М. Терехов, О.И. Осипов; Под ред. В.М. Терехова. - – М.: Издательский центр <<Академия>>, 2005. – 304 с.

8. Соколовский Г.Г. Электроприводы переменного тока с частотным регулированием: учебник для студ. высш. учеб. заведений/Г.Г. Соколовский. – М.: Издательский центр <<Академия>>, 2006. – 272 с.

9. Воронов А.А. Основы теории автоматического управления []Текст]. Часть 1. Линейные системы регулирования одной величины. М.-Л., Энергия, 1965. Часть 2. Специальные линейные и нелинейные системы автоматичес- кого регулирования одной величины, 1966. Часть 3. Оптимальные многосвязанные и адаптивные системы, Л- Энергия, 1970.

10. Методы классической и современной теории автоматического управления. Учебник в пяти томах. Под ред. К.А. Пупкова. М.: Издательство МГТУ им. Н.Э. Баумана, 2004.

11. Лукас В.А. Теория управления техническими системами. [Текст] - Екатеринбург: Изд-во УГГГА, 2002.

12. Ротач В.Я. Теория автоматического управления: Учебник для вузов [Текст] – 2-е изд., перераб. и доп. – М.: Издательство МЭИ, 2004. – 400 с., ил.

13. Трофимов А.И., Егупов Н.Д., Дмитриев А.Н. Методы теории автоматического управления, ориентированные на применение ЭВМ. Линейные стационарные и нестационарные модели [Текст]: Учебник для вузов. – М.: Энергоатомиздат, 1997. – 656 с.: ил.

14. Кулаков Г.Т. Анализ и синтез систем автоматического регулирования [Текст]: Учеб. пособие / Г.Т. Кулаков. – Мн.: УП “Технопринт”, 2003. – 135 с.

15. Медведев В.С., Потёмкин В.Г. Control System Toolbox. MATLAB 5 для студентов. [Текст] –М.: ДИАЛОГ - МИФИ, 1999.

16. Дьяконов В., Круглов В. Математические пакеты расширения MATLAB. Специальный справочник. [Текст] –СПб.: Питер, 2001.

17. Дьяконов В., Круглов В. MATLAB. Анализ, идентификация и моделирование систем. Специальный справочник. [Текст] – СПб.: Питер, 2002.

18. Дьяконов В. Simulink 4. Специальный справочник. [Текст]–СПб.: Питер, 2002.

19. В. П. Дьяконов. MATLAB 6.5 SP1/7 + Simulink 5/6. Основы применения. Серия <<Библиотека профессионала>>. –М.: СОЛОН-Пресс, 2005. – 800 с.: ил.

20. В. П. Дьяконов. MATLAB 6.5 SP1/7 + Simulink 5/6 в математике и моделировании. Серия <<Библиотека профессионала>>. –М.: СОЛОН-Пресс, 2005. – 576 с.: ил.

21. Филлипс Ч., Харбор Р. Системы управления с обратной связью. [Текст] М.: Лаборатория Базовых Знаний, 2001.

22. Дорф Р. Современные6 системы управления [Текст] / Р. Дорф, Р. Бишоп. Пер. с англ. Б.И. Копылова. – М.: Лаборатория Базовых Знаний, 2002. – 832 с.: ил.

23. Юревич Е.И. Теория автоматического управления. – 3-е изд. – СПб.: БХВ-Петербург, 2007. – 560 с.: ил.

21. Власов К.П. Теория автоматического управления. Учебное пособие. Х.: Изд-во Гуманитарный центр, 2007, 526 с.

24. Востриков А.С., Французова Г.А. Теория автоматического ренулирования:Учеб. пособие. – Новосибирск: Изд-во НГТУ, 2003. - 364 с.

25. Савин М.М. Теория автоматического управления: учеб. пособие / М.М. Савин, В.С. Елсуков, О.Н. Пятина; под ред. д.т.н., проф. В.И. Лачина. – Ростов н/Д: Феникс, 2007.- 469 с.: ил.

26. Интрилигатор М. Математические методы оптимизации и экономическая теория [Текст]/ Пер. с англ. Г.И. Жуковой, Ф.Я. Кельмана. – М.: Айрис-пресс, 2002. – 576 с.: ил. – (Высшее образование).

27. Автухов В.В. Метод отыскания оптимального и компромиссного законов управления объектами автоматического регулирования [Текст]. Изв. вузов, Цветная металлургия, 1984, №2, с. 111-117.

28. Поляк Б.Т. Робастная устойчивость и управление. [Текст]. /Б.Т. Поляк, П.С. Щербаков. – М.: Наука, 2002. – 303 с.

29. Гудвин Г.К. Проектирование систем управления/Г.К. Гудвин, С.Ф. Гребе, М.Э. Сальгадо. – М.: БИНОМ. Лаборатория знаний, 2004. – 911 с., ил.

30. Осипов В.М., Кибардин В.В., Буралков А.А. Методы оптимизации в электротехнике: Учеб. пособие/ ГАЦМиЗ. – Красноярск, 2001. – 156 с.

Приложение 1

Дата добавления: 2015-08-31