Розділ 5. Побудова годографа амплітудно-фазової частотної характеристики розімкнутої системи і визначення запасу стійкості

Передаточна функція розімкненої системи має вигляд:

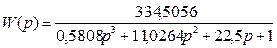
Щоб виділити цілу і уявну частини, замінимо р=јω.

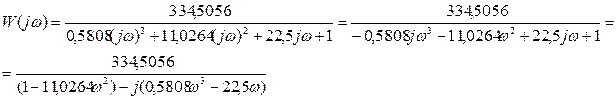
Щоб позбутися комплексної одиниці в знаменнику домножимо дріб на спряжений до знаменника вираз:

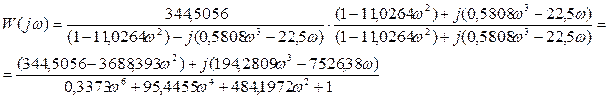Виділимо дійсну та уявну частини W (jω)= Р (ω)+ jQ (ω):

Р (ω)= 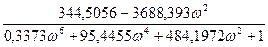– дійсна частотна характеристика;

Q (ω)= 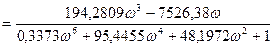– уявна частотна характеристика.

Підставивши ω отримаємо наступні значення

Таблиця 5.1

Область значень Р(ω) та Q(ω)

ω		0,005	0,0075	0,025	0,05	0,075	0,1	0,2	0,5
Р (ω)	334,50	330,413	325,434	255,016	147,115	84,1936	50,8623	9,1113	-4,5898	-5,7728
Q (ω)		-37,181	-54,951	-144,44	-170,18	-151,45	-128,58	-73,278	-29,205	-12,620

1,5
-5,0488	-4,13568	-1,19272	-0,27496	-0,09445	-0,03981	-0,01026	-0,00157
-6,74105	-3,87164	-0,17627	0,088805	0,0618	0,037883	0,015509	0,004074

Годограф виглядає наступним чином:

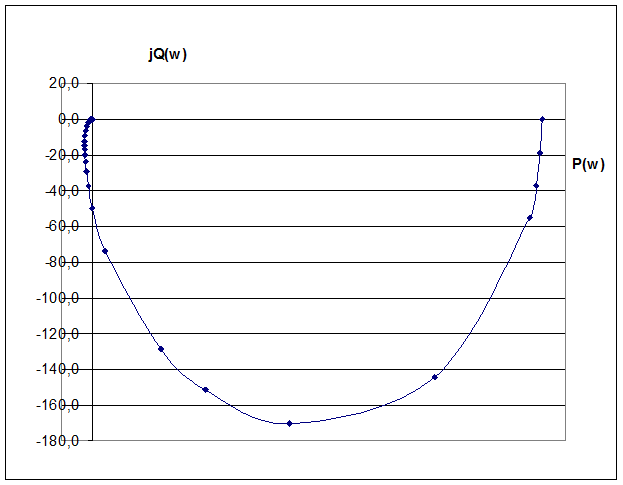Рис 5.1. Годограф амплітудно-фазової частотної характеристики розімкнутої системи

Для визначення запасів стійкості використаємо критерій Найквіста.

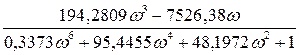Для визначення запасу стійкості за амплітудою знайдемо частоту, яка відповідає точці перетину годографа АФЧХ з від'ємною дійсною піввіссю (з умови jQ () = 0):

=0

Знайдемо корені чисельника. Для цього прирівняємо його до нуля:

=0

Маємо: ω ₁=0; ω ₂=-6,224; ω ₃=6,224.

Нас задовольняє лише ω ₃=6,224, оскільки частота не може бути від’ємною. При такому значення ω Р (6,224)= - 0,7849138.

Отже запас стійкості за амплітудою А_зап=1- 0,7849138=0,215

Побудуємо одиничне коло і проведемо пряму, яка проходить через точку перетину цього кола з годографом, щоб визначити запас стійкості по фазі.

Як бачимо годограф перетинає коло одиничного радіусу у точці (-0,996;-0,089)

Для визначення запасу стійкості за амплітудою використаємо наступну залежність:

φ=arctg(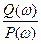)=arctg(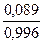)=5,106

Отже φ=5,106°

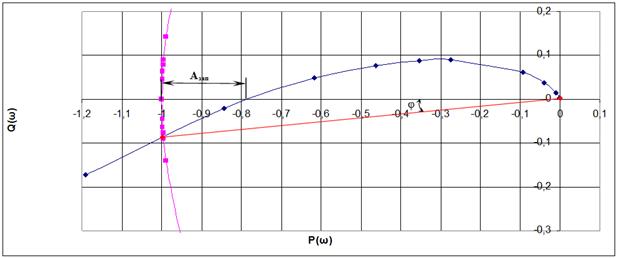
Рис 5.2. Графік перетину годографа та одиничного кола

Висновок: з графіка видно, що запас стійкості за амплітудою становить А_зап=0,215, а запас стійкості за фазою становить φ =5,106°.

Дата добавления: 2015-08-31