Применение правила Вант-Гоффа и уравнения Аррениуса

Влияние температуры на скорость химических реакций.

Скорость химических реакций увеличивается с ростом температуры. Экспериментально установлено, что при увеличении температуры на десять градусов скорость гомогенной реакции возрастает в 2¸4 раза. Эта закономерность называется правилом Вант-Гоффа. Число, показывающее, во сколько раз возрастает константа скорости при повышении температуры на десять градусов, называется температурным коэффициентом константы скорости и обозначается g:

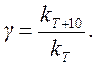(4.11)

Это правило является приближенным, так как температурный коэффициент сохраняет постоянное значение только в узкой температурной области. Правило Вант-Гоффа можно записать следующим образом:

или (4.12)

Более точную зависимость константы скорости химической реакции от температуры установил Аррениус, предложивший уравнение

(4.13)

где Е – энергия активации; k –константа скорости.

Энергией активации называется минимальное избыточное количество энергии молекул (по сравнению со средней), необходимое для их вступления в химическую реакцию.

Определенное интегрирование уравнения (4.13) позволяет получить

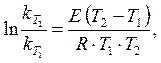(4.14)

или

(4.15)

где и – константы скорости реакции при температуре Т₁ и Т₂.

Понятие «энергия активации» было введено Аррениусом в теории активных столкновений (ТАС), сущность которой состоит в следующем: химическое взаимодействие осуществляется только при взаимодействии активных частиц, которые обладают достаточной энергией для преодоления потенциального барьера реакции и ориентированы в пространстве определенным образом относительно друг друга.

Зависимость константы скорости от температуры определяется уравнением, которое может быть получено при неопределенном интегрировании уравнения Аррениуса (4.13):

(4.16)

где k – константа скорости реакции;

А – предэкспоненциальный множитель.

Постоянные А и Е обычно определяют опытным путем по температурной зависимости константы скорости реакции. Для этого уравнение (4.16) можно записать в форме:

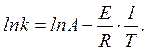(4.17)

Откладывая на оси ординат ln k, а по оси абсцисс , получают прямую линию, тангенс угла наклона которой из этого соотношения находят Отрезок, отсекаемый продолжением прямой до пересечения с осью ординат (1/Т = 0), соответствует величине lnA. Отсюда можно рассчитать предэкспоненциальный множитель А.

П р и м е р 4.6. Для одной и той же реакции определены две константы скорости при двух температурах: 0,00312 мин^-1 при 288 К (Т₁) и 0,00838 мин^-1 при 300 К (Т₂). Вычислить энергию активации, температурный коэффициент и константу скорости при температуре 320 К. Расчет константы скорости выполнить двумя методами: по уравнению Вант–Гоффа и с применением уравнения Аррениуса.

Дата добавления: 2017-01-14