Законы электролиза Фарадея и их применение для расчета количественных характеристик процесса электролиза

Тогда

, (3.53)

а сама константа равновесия:

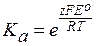. (3.54)

П р и м е р 3.11. Рассчитать потенциал кадмиевого электрода, опущенного в водный раствор сульфата кадмия с активностью ионов кадмия 0,015, при температуре 30 ^ОС (303 К).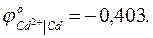

Р е ш е н и е

Электродная реакция может быть записана следующим образом:

Cd²⁺ + 2 e ^– ↔ Cd.

Количество электронов, участвующих в данной электродной реакции, z = 2.

Равновесный электродный потенциал рассчитываем по уравнению Нернста:

,

П р и м е р 3.12. Рассчитать ЭДС гальванического элемента, составленного из полуэлементов Zn²⁺│Zn и Cu²⁺│Cu при температуре 20 ^оС, если активности ионов цинка и меди равны 0,1 и 0,05, соответственно.

Р е ш е н и е

Zn – 2 e ^– ↔ Zn²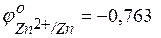⁺; В,

Cu²⁺ + 2 e ^– ↔ Cu; .

Находим стандартную ЭДС:

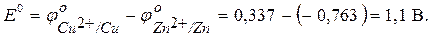
Для данного гальванического элемента z = 2; T = 293 K.

ЭДС гальванического элемента рассчитываем по уравнению (3.39):

.

П р и м е р 3.13. Как должен быть записан гальванический элемент, состоящий из хлорсеребряного и каломельного электродов, в котором протекает следующая химическая реакция:

2Ag + Hg₂Cl₂ ↔ 2 AgCl + 2 Hg.

Чему равна стандартная ЭДС этого элемента?

Р е ш е н и е

При работе гальванического элемента серебро окисляется, а ртуть восстанавливается:

2 Ag – 2 e^– → 2 Ag⁺ (ионы переходят в раствор)

2 Hg⁺ + 2 e^– → 2 Hg,

следовательно, хлорсеребряный электрод – отрицательный, а каломельный является положительным электродом. Поэтому гальванический элемент должен быть записан следующим образом:

Ag│AgCl, KCl║ KCl, Hg₂Cl₂│Hg.

Стандартные потенциалы электродных реакций:

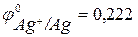В, В.

Стандартная ЭДС гальванического элемента:

В.

П р и м е р 3.14. Написать химическую реакцию, протекающую в данном гальваническом элементе в стандартных условиях:

Pt│H⁺, MnO₄^–, Mn²⁺ ║ Co³⁺, Co²⁺│Pt.

Р е ш е н и е

В таблице стандартных потенциалов находим потенциалы электродных реакций, соответствующих данному гальваническому элементу:

MnO₄^– + 8 H ⁺ + 5 e^– ↔ Mn²⁺ + 4 H₂O; 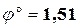В;

Co³⁺ + e ^– ↔ Co²⁺; В.

Так как при записи гальванического элемента сначала указывается более отрицательный электрод, на котором происходит окисление, следовательно, эта запись соответствует окислению ионов марганца Mn²⁺ и восстановлению ионов кобальта Co³⁺.

Тогда протекающая в элементе реакция должна быть записана следующим образом:

5Co³⁺ + Mn²⁺ + 4 H₂O = 5 Co²⁺ + 8 H⁺ + MnO₄^–.

П р и м е р 3.15. Для химической реакции

Pb + Hg₂Cl₂ = PbCl₂ + 2 Hg,

протекающей обратимо в гальваническом элементе, зависимость ЭДС от температуры описывается уравнением E = 0,5353 + 1,45·10^–4 Т. Рассчитать при температуре 298 К ЭДС гальванического элемента, изменение энергии Гиббса, изменение энтропии, изменение энтальпии и количество теплоты, которое будет поглощаться в этом процессе.

Р е ш е н и е

Находим ЭДС гальванического элемента, подставляя в известное уравнение зависимости Е = f(T) заданную температуру:

E = 0,5353 + 1,45·10^–4 · 298 = 0,5353 + 0,0432 = 0,5785 B.

В гальваническом элементе будут происходить следующие реакции:

Pb – 2 e^– = Pb²⁺ (окисление); 2 Hg⁺ + 2e^– = 2Hg (восстановление); z = 2.

Рассчитываем изменение энергии Гиббса по формуле (3.43)

∆G = – z · F · E = – 2 · 96485 · 0,5785 = – 111633 Дж/моль.

Температурный коэффициент ЭДС находим, дифференцируя по температуре известное из условия уравнение зависимости Е = f(T):

= 1,45·10^–4 В/K.

Изменение энтропии находим по формуле (3.45):

.

Изменение энтальпии ∆H рассчитываем по формуле (3.48):

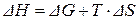= – 111633 + 298 · 27,98 = – 103295 Дж/моль.

Рассчитываем связанную энергию процесса:

T ·ΔS = 298 · 27,98 = 8338 Дж/моль.

Так как > 0, то такое количество энергии будет поглощаться при работе гальванического элемента.

П р и м е р 3.16. Рассчитать константу равновесия при стандартных условиях следующей окислительно-восстановительной реакции:

Zn + 2 HCl ↔ ZnCl₂ + H₂.

Р е ш е н и е

Данная реакция может быть осуществлена в следующем гальваническом элементе:

Zn│ZnCl₂║H⁺│H₂, Pt.

Уравнения полуреакций и соответствующие им стандартные потенциалы, значения которых взяты из справочной таблицы, выглядят так:

2 H⁺ + 2 e ^– ↔ H₂; В;

Zn²⁺ + 2 e ^– ↔ Zn; В.

Тогда стандартная ЭДС гальванического элемента определяется следующим образом:

В.

Константу равновесия рассчитываем, используя уравнения (3.53) и (3.54):

; .

Высокое значение константы равновесия свидетельствует о практической необратимости реакции вытеснения водорода цинком при стандартной температуре.

П р и м е р 3.17. Может ли железо вытеснить медь из раствора сульфата меди? Чему равна константа равновесия этой реакции при стандартной температуре?

Р е ш е н и е

Уравнение окислительно-восстановительной реакции выглядит так:

Fe + Cu²⁺ ↔ Fe²⁺ + Cu.

Полуреакции и соответствующие им стандартные потенциалы определяется так:

Fe²⁺ + 2 e ^– ↔ Fe;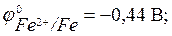

Cu²⁺ + 2 e ^– ↔ Cu;

При протекании данной реакции в гальваническом элементе:

Fe│FeSO₄║CuSO₄│Cu

его стандартная ЭДС находится из уравнения

Константу равновесия рассчитываем, используя уравнения (3.53) и (3.54):

Значение константы равновесия показывает, что процесс вытеснения меди из раствора железом протекает при стандартной температуре практически полностью.

Электролизом называется совокупность электрохимических окислительно-восстановительных реакций, протекающих на электродах при прохождении постоянного электрического тока через раствор или расплав электролита. При этом на катоде происходит процесс восстановления, а на аноде – окисления. Катионы восстанавливаются в ионы более низкой степени окисления или в атомы, например:

Fe³⁺ + e ^– → Fe²⁺; (3.55)

Cu²⁺ + 2 e ^– → Cu. (3.56)

Нейтральные молекулы могут участвовать в превращениях на катоде непосредственно или взаимодействовать с продуктами катодного процесса, которые рассматриваются в этом случае как промежуточные вещества. Например, восстановление воды:

2 H₂O + 2 e ^– → H₂ + 2 OH^–. (3.57)

На аноде окисляются ионы или молекулы, поступающие из объема электролита, например:

4 OH^– – 4 e ^– → 2 H₂O + O₂; (3.58)

2 Cl^– – 2 e ^– → Cl₂,– (3.59)

или принадлежащие материалу анода. в последнем случае анод растворяется, например:

Cu – 2 e ^– → Cu²⁺ (растворение медного анода). (3.60)

Протекание электродных реакций зависит от состава и концентрации электролита, материала электродов, электродного потенциала, температуры, гидродинамических условий.

Процессы электролиза описываются законами Фарадея, которые в объединенной форме читаются следующим образом: массы веществ, испытавших электрохимические превращения на электродах, прямо пропорциональны количеству протекшего через электролит электричества и электрохимическим эквивалентам этих веществ:

(3.61)

где m – масса вещества, превратившегося на электроде (выделившегося на электроде),

электрохимический эквивалент – величина характеризующая массу продуктов электролиза, выделившихся на электродах при прохождении через электролит 1 Кл электричества;

Э – химический эквивалент вещества (эквивалентная масса вещества) при окислительно-восстановительном превращении, г/экв;

q – количество прошедшего электричества, Кл;

F – число Фарадея (96485 Кл/г-экв) – количество электричества, необходимое для химического превращения (выделения на электроде) 1 г-экв вещества.

Так как q = I · τ (I – сила тока, А; τ – продолжительность электролиза, с), то уравнение закона Фарадея может быть записано следующим образом:

(3.62)

Химический эквивалент вещества (эквивалентная масса вещества) при окислительно-восстановительном превращении рассчитывается по формуле:

, (3.63)

где М – молярная масса вещества, претерпевающего превращение на электроде, г/моль;

n – количество электронов, участвующих в одном акте химического превращения.

По законам Фарадея (3.61) и (3.62) рассчитываются теоретически возможные количества превращающихся веществ на электродах. На практике при электрохимических процессах наблюдаются отклонения от законов Фарадея: масса действительно полученного или разложившегося продукта может не соответствовать теоретической. Эти отклонения – кажущиеся и возникают за счет одновременного протекания побочных электрохимических процессов; химических реакций, в которые вступает продукт; потерь продукта и потерь электроэнергии на преодоление сопротивления электролизера. Эффективность электрохимического процесса оценивается выходом по току В_т:

(3.64)

Эта величина может быть выражена в процентах:

. (3.65)

Тогда практическое количество вещества, образующееся при электролизе рассчитывается по формуле:

. (3.66)

П р и м е р 3.18. Какое количество алюминия выделится при электролизе за время 12 ч, если сила тока I = 2,5 A, а выход по току составляет 88 %. Молярная масса алюминия М, равная его грамм-атомной массе А, составляет 26,98 г/моль.

Р е ш е н и е

Выделение алюминия при электролизе происходит на катоде при прохождении следующей реакции восстановления:

Al³⁺ + 3 e ^– = Al; n = 3.

Химический эквивалент алюминия рассчитываем по формуле (3.62):

Э = М / 3 = 26,98 / 3 = 8,99 г/экв.

Продолжительность электролиза τ = 12 час = 12 · 3600 = 43200 с.

По объединенному закону Фарадея (3.62) находим теоретическое количество алюминия, выделяющееся при электролизе в указанных условиях:

г.

Практическое количество выделившегося при электролизе алюминия находим с учетом величины В_Т по формуле (3.66):

П р и м е р 3.19. Определить время, необходимое для выделения при электролизе 1,2 г меди, если сила тока I = 2 A, а выход по току В_Т = 96 %.

Р е ш е н и е

На основании формулы (3.66) находим, на какое теоретическое количество меди необходимо рассчитывать продолжительность электролиза:

Выделение меди при электролизе происходит на катоде при прохождении следующей реакции восстановления:

Сu²⁺ + 2 e ^– = Cu; n = 2.

Химический эквивалент меди рассчитываем по формуле (3.63):

Э = М / 2 = 63,54 / 2 = 31,77 г/экв.

Из уравнения закона Фарадея (3.62) находим время процесса:

1. ХИМИЧЕСКАЯ КИНЕТИКА

Химическая кинетика – раздел физической химии, в котором рассматривается зависимость скорости химической реакции от концентрации реагентов, температуры, свойств среды и других факторов.

Дата добавления: 2017-01-14