Расчет характеристик растворов электролитов

Р е ш е н и е

Найдем мольную долю растворенного вещества в данном растворе, для чего воспользуемся уравнением закона Рауля (2.7):

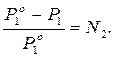
По условию задачи P₁ на 2 % ниже , то есть составляет , тогда:

Отсюда N₂ = 0,02.

Для определения моляльности m рассчитаем количество молей растворенного вещества n₂, приходящееся в растворе на 1000 г воды. В этом случае m = n₂.

Количество молей воды в 1000 г составляет:

n₁ = g₁/M₁ = 1000/ 18 = 55,55 моль.

В соответствии с определением (2.2) запишем выражение для мольной доли растворенного вещества:

в которое подставим значение n₁, а вместо n₂ – m, и найдем эту величину:

отсюда m = 0,02 · (55,55 + m); 0,98 · m = 1,111;

m = 1,134 моль/1000 г воды.

П р и м е р 2.3. Рассчитать общее давление насыщенного пара над бинарным совершенным раствором при температуре 313 К, состоящим из 200 г дихлорэтана C₂H₄Cl₂ (ДХЭ) и 350 г бензола C₆H₆ (Б), если давления насыщенного пара над этими чистыми веществами при указанной температуре составляют: Р^о_ДХЭ = 2,066·10⁴ Па и = 2,433·10⁴ Па.

Р е ш е н и е

Молярные массы веществ: M_ДХЭ = 99 г/моль; M_Б = 78 г/моль.

Находим количества молей компонентов в растворе:

n_ДХЭ = 200/ 99 = 2,020 моль; n_Б = 350/ 78 = 4,487 моль;

суммарное количество молей веществ:

n_ДХЭ + n_Б = 2,020 + 4,487 = 6,507 моль.

Рассчитаем мольные доли каждого компонента в растворе:

N_ДХЭ = 2,020/6,507 = 0,31; N_Б = 4,487/6,507 = 0,69.

Давление насыщенного пара над раствором каждого компонента находится по уравнению закона Рауля для совершенных растворов (2.7):

Общее давление рассчитываем по уравнению (2.8):

P = P_ДХЭ + P_Б = 0,640 · 10⁴ + 1,679 · 10⁴ = 2,319 · 10⁴ Па.

П р и м е р 2.4. Рассчитать температуру замерзания (кристаллизации) 1 % раствора серы S в железе Fe, если температура кристаллизации чистого железа составляет 1813 К, а его К_кр. = 101,5 К/моль. Молярная масса серы 32 г/моль.

Р е ш е н и е

Если данный раствор содержит 1 % растворенного вещества, то в 100 г этого раствора содержится 1 г серы (g₂) и 99 г железа (g₁). Рассчитаем моляльность раствора серы в железе по уравнению (2.5):

Понижение температуры замерзания рассчитываем по уравнению (2.12):

ΔT_зам. = К_кр. · m = 101,5 · 0,316 = 32,07 К.

Температура замерзания раствора серы в железе:

Т_зам. = Т^о_зам. – ΔT_зам = 1813 – 32,07 = 1780,93 К = 1507,73 ^оС.

П р и м е р 2.5. Рассчитать, какое количество этиленгликоля C₂H₄(OH)₂ необходимо добавить к 500 г воды (g₁), чтобы понизить температуру замерзания раствора на 3 градуса. Криоскопическая константа воды К_кр. = 1,86 град/моль. Молярная масса этиленгликоля М₂ = 62 г/моль.

Р е ш е н и е

Находим моляльность раствора по уравнению (2.15):

Из формулы (2.5) для расчета моляльности:

,

выражаем и рассчитываем величину g₂:

П р и м е р 2.6. Вычислить молярную массу вещества, если температура замерзания раствора, содержащего 200 г бензола (g₁) и 0,4 г исследуемого вещества (g₂), на 0,17 К ниже температуры замерзания бензола. Криоскопическая константа бензола К_{кр .} = 5, 16 К/моль.

Р е ш е н и е

Расчет производим по формуле (2.18) для криоскопии:

П р и м е р 2.7. Вычислить кажущуюся степень диссоциации соли BaCl₂ в 3,2%-ном водном растворе, если температура кипения водного раствора равна 100,21 ^оС. Молярная масса хлорида бария 208 г/моль. Эбулиоскопическая константа воды К_{эб .} = 0,512 град/моль.

Р е ш е н и е.

Определим моляльность раствора по формуле:

Расчет выполняем для 100г раствора. При указанной массовой концентрации содержание BaCl₂ в этом количестве раствора составит 3,2 г (g₂), а растворителя – воды g₁ = 100 – 3,2 = 96,8 г;

моль/1000 г воды.

ΔT_кип = 100,21 – 100 = 0,21 ^оС (К),

где 100 ^оС – температура кипения чистого растворителя (воды).

Находим изотонический коэффициент из уравнения (2.17):

.

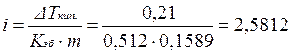Степень диссоциации α находим из соотношения (2.10):

;

для BaCl₂ ν = 3, так как при диссоциации одной молекулы этой соли образуются три иона;

.

Найденная степень диссоциации для сильного электролита является кажущейся, а истинная близка к 1.

1. ЭЛЕКТРОХИМИЯ

Электролитами называются вещества, которые в растворе или расплаве распадаются на ионы – заряженные частицы (положительные – катионы, отрицательные – анионы). Процесс распада растворенного вещества на ионы самопроизволен и называется электролитической диссоциацией. Диссоциация количественно характеризуется величиной степени диссоциации α, которая представляет собой отношение числа диссоциированных молекул к их общему числу в растворе. По степени диссоциации электролиты делятся на слабые (α £ 0,02) и сильные (α ³ 0,5).

К процессу диссоциации применим закон действующих масс. В случае 1,1-валентного электролита АВ с исходной концентрацией С (г-экв/л) равновесие при диссоциации имеет вид:

АВ ↔ А⁺ + В^-. (3.1)

Выражение для константы равновесия этого процесса К_Д (константы дисоциации) записывается следующим образом:

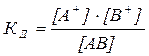, (3.2)

где [А⁺], [В^-], [АВ] – равновесные концентрации катионов, анионов и недиссоциированных молекул, которые при степени диссоциации α могут быть выражены следующим образом:

[А⁺] = α · С, [В^-] = α · С, [АВ] = (1 - α) · С, (3.3)

тогда после подстановки этих величин в уравнение (3.2) и сокращения на величину С получим выражение:

. (3.4)

Уравнение (3.4) может быть записано с введением понятия разведения. Разведение – это объем раствора данной концентрации, содержащий 1 г-эквивалент растворенного вещества:

(3.5)

Тогда

(3.6)

Константа равновесия диссоциации К_Д – это величина, зависящая от природы электролита, природы растворителя и температуры. Значения К_Д для электролитов приводятся в справочниках. Уравнения (3.4) и (3.6) известны как математические выражения закона разведения Оствальда.

Уравнение (3.4) может быть использовано для расчета степени диссоциации слабого электролита при заданной концентрации раствора по известной константе диссоциации. В этом случае решается квадратное уравнение:

Сα² + К_Д α – К_Д = 0. (3.7)

По найденному значению степени диссоциации и известной концентрации электролита могут быть рассчитаны концентрации ионов в растворе. Концентрации ионов Н⁺ или ОН ^– служат для характеристики среды (кислая, нейтральная, щелочная). По ним могут быть рассчитаны водородный рН или гидроксильный показатели рОН:

, (3.8)

. (3.9)

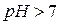В случае ( г-ион/л) среда нейтральная, при ( г-ион/л) среда кислая, при ( г-ион/л) среда щелочная. Сумма показателей: pH + pOH = 14.

Как указывалось в главе 2, Вант-Гофф ввел понятие об изотоническом коэффициенте i, который показывает, во сколько раз увеличивается число частиц в растворах электролитов за счет диссоциации. Изотонический коэффициент связан со степенью диссоциации α соотношением (2.10).

Растворы электролитов относятся к реальным раствором, так как в них существует взаимодействие между ионами, а также между ионами и молекулами растворителя. Для оценки отклонения свойств реальных растворов от свойств идеальных систем введено понятие термодинамической активности, которое используется в расчетах вместо концентрации и связано с ней коэффициентом термодинамической активности (γ):

. (3.10)

Концентрация растворов может выражаться при этом разными способами. Коэффициент термодинамической активности характеризует степень отклонения свойств реальных растворов от свойств идеальных систем. Активность и коэффициент активности зависят от природы, количественного состава растворов и от температуры. Они определяются опытным путем при изучении равновесий в растворах.

Для описания свойств растворов электролитов введено понятие средней активности ионов :

, (3.11)

где – количество катионов и количество анионов, образующихся при диссоциации молекулы электролита; .

Средняя ионная активность связана со средней концентрацией (средней моляльностью) раствора m_± и средним коэффициентом активности ионов соотношением:

. (3.12)

Каждая из этих средних величин представляет собой среднее геометрическое из соответствующих величин для катионов и анионов:

(3.13)

, (3.14)

где – моляльность катиона, – моляльность аниона, а

m – моляльность раствора электролита.

Средние ионные коэффициенты активности могут быть найдены различными экспериментальными методами, а также рассчитаны, например, на основании электростатической теории, которая была создана Дебаем и Гюккелем для описания свойств реальных растворов электролитов.

П р и м е р 3.1. Найти выражения для средних величин: γ_± , m_± , a_±, и a_общ. для электролита KCl, моляльность которого m.

Р е ш е н и е

Электролит KCl относится к валентному типу 1,1.

ν₊ = 1, ν_- = 1, ν = ν₊+ν_- = 2.

= = ;

=

a_± = m_± · γ_± = m · (γ₊γ_-)^1/2;

a_общ.= a_± = = .

П р и м е р 3.2. Определить концентрацию гидроксида аммония в воде, при которой он диссоциирован на 1% (α = 0,01). Константа диссоциации К_Д = 1,79·10 ^{– 5}.

Р е ш е н и е

Гидрооксид аммония – 1,1- валентный электролит, диссоциирующий следующим образом:

NH₄OH ↔ NH₄⁺ + OH^–.

Для решения задачи воспользуемся формулой (3.4):

,

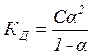откуда, выразив концентрацию С, получаем:

моль/л (г-экв/л).

П р и м е р 3.3. Вычислить рН раствора муравьиной кислоты концентрации 0,3 моль/л. Константа диссоциации кислоты 1,772·10^-4.

Р е ш е н и е

Муравьиная кислота диссоциирует по схеме:

HCOOH ↔ H⁺ + HCOO^–.

Находим степень диссоциации, решая уравнение (3.7):

Сα² + К_Д α – К_Д = 0,

в которое подставляются известные значения С и K_Д:

0,3 α ² + 1,772·10^-4 α – 1,772·10^-4 = 0.

Находим корни этого квадратного уравнения. Физический смысл имеет только положительный корень: α = 0,024.

Так как при диссоциации 1 моля муравьиной кислоты образуется 1 моль ионов водорода, то концентрация ионов водорода:

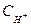= C · α = 0,3 · 0,024 = 7,2·10^-3;

Находим рН раствора:

= 2,1427 ~ 2,14 < 7 (кислая среда).

Дата добавления: 2017-01-14