Свойства растворов

Р е ш е н и е

Р е ш е н и е

Р е ш е н и е

Термодинамические свойства веществ

Вещества	Количество молей νi	, кДж/моль	, Дж/(моль·К)
Al2O3		–1675,69	50,92
SO3		–395,85	256,69
Al2(SO4)3		–3441,80	239,20

Находим стандартный тепловой эффект в виде изменения энтальпии по известным теплотам образования по формуле (1.17):

ΔН^о₂₉₈ = –3441,80 – (–1675,69 + 3 · (–395,85)) = –578,56 кДж.

Стандартное изменение энтропии находим по формуле (1.38):

ΔS^о₂₉₈

Стандартное изменение энергии Гиббса при Т = 298 К рассчитаем по уравнению (1.43):

ΔG^о₂₉₈ = –578,56 · 10³ – 298 · (– 581,79) = – 405186,6 Дж.

Расчет К_P производится по уравнениям (1.62):

Высокое значение константы равновесия свидетельствует о том, что равновесие практически полностью смещено в сторону конечных продуктов, и данная реакция по сути является необратимой.

П р и м е р 1.19. Рассчитать константы равновесия для химической реакции примера 1.15:

TiO₂ + 2H₂ = Ti + 2H₂O.

кр. газ кр. газ

при температурах 298 К и 1800 К. Записать закон действующих масс для данной гетерогенной реакции.

Расчет производится по уравнениям (1.62), в которые подставляют значения ΔG^о_Т (пример 1.16), соответствующие температурам, для которых выполняется расчет:

Закон действующих масс для данной гетерогенной реакции записывается только через равновесные парциальные давления газообразных веществ (оксид титана и титан находятся в твердом состоянии):

Расчет показал, что с увеличением температуры константа равновесия увеличилась (данная реакция является эндотермической). Однако и при стандартной температуре, и при температуре 1800 К константа равновесия << 1, то есть при данных температурах равновесие смещено в сторону исходных реагентов (реакция практически не идет).

П р и м е р 1.20. Определить, в каком направлении будет протекать при температуре 873 К химическая реакция

COCl₂ ↔ CO + Cl₂

при следующих заданных значениях неравновесных парциальных давлений компонентов (Н/м²), находящихся в газовой фазе: = 1,048·10⁵; = 3,039·10⁵; = 3,039·10⁵. Константа равновесия K_P при данной температуре равна 5,833·10⁵ Н/м².

Константа равновесия для данной реакции:

.

Проводим расчет изменения энергии Гиббса по уравнению (1.60):

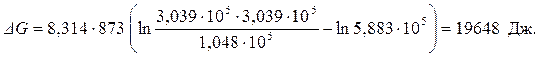
Так как для данной реакции ΔG > 0, то при указанных исходных значениях неравновесных парциальных давлений процесс возможен только в обратном направлении.

1.7. Фазовые равновесия в однокомпонентных системах. Уравнение Клапейрона–Клаузиуса и его применение для расчета теплоты испарения, давления насыщенного пара и температуры кипения

Фазовые равновесия в однокомпонентных системах – это равновесия в гетерогенных системах, в которых протекают процессы перехода компонента из одной фазы в другую.

В однокомпонентных системах различают следующие фазовые переходы:

жидкость ↔ пар (испарение и конденсация);

тв. вещество ↔ пар (возгонка и сублимация);

тв. вещество ↔ жидкость (плавление и кристаллизация);

тв. вещество ↔ тв. вещество (полиморфные превращения).

Фазовые переходы сопровождаются тепловыми эффектами и происходят при определенных температурах (Т). Температурой фазового перехода называется температура, при которой соответствующие фазы находятся в равновесии. Эта температура зависит от внешнего давления (Р). Взаимосвязь Р и Т при равновесии между двумя фазами описывается уравнением Клапейрона–Клаузиуса:

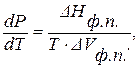(1.65)

где P и T – давление и температура при фазовом переходе;

ΔH_ф.п. – изменение энтальпии 1 моля вещества при фазовом переходе (мольный тепловой эффект фазового перехода при P = const);

ΔV_ф.п. – разность мольных объемов фаз, находящихся в равновесии.

Для процесса испарения и возгонки уравнение (1.65) может быть преобразовано и имеет вид:

(1.66)

где ΔH_{ф.п .} – изменение энтальпии 1 моля вещества при испарении (теплота испарения) или возгонке (теплота возгонки).

В настоящем пособии рассматривается применение уравнения (1.66) для процесса испарения.

Пар, находящийся в динамическом равновесии с жидкостью, из которой он образовался, называется насыщенным паром, а давление, которое оказывает пар, находящийся в равновесии с жидкостью, на поверхность жидкости и стенки сосуда называется давлением насыщенного пара. Температура кипения – это температура перехода вещества из жидкого состояния в парообразное, при которой давление насыщенного пара жидкости равняется внешнему давлению. При кипении испарение происходит по всему объему, а не только с поверхности жидкости

Уравнение Клапейрона–Клаузиуса позволяет рассчитывать теплоты испарения индивидуальных веществ, давление их насыщенного пара при различных температурах, температуры кипения веществ при различных давлениях.

Для расчетов применяется интегральная форма уравнения Клапейрона–Клаузиуса. В небольшом интервале температур DН_исп можно считать постоянной. В точных расчетах необходимо учитывать зависимость теплоты испарения от температуры. Интегрирование уравнения Клапейрона-Клаузиуса в пределах от Т₁ до Т₂, которым соответствуют давления Р₁ и Р₂, при постоянном значении DН_исп позволяет получить уравнения:

, (1.67)

. ( 1.68)

Уравнение (1.68) может быть использовано для расчета DН_исп, если известны давления насыщенного пара при двух температурах:

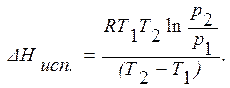(1.69)

Из уравнений (1.67) и (1.68) можно по известной теплоте испарения и данных о давлении насыщенного пара при одной температуре рассчитывать давление насыщенного пара при другой температуре или температуру кипения при заданном внешнем давлении.

При неопределенном интегрировании уравнения Клапейрона-Клаузиуса получим:

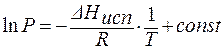. (1.70)

Обозначим величину А, а константу интегрирования В. Тогда

. (1.71)

Уравнение (1.71) позволяет вычислить давление насыщенного пара над жидкостью при любой температуре, если известны константы А и В, которые определяют на основе экспериментальных данных аналитическим или графическим методом по найденным экспериментально значениям температур кипения, по крайней мере, при двух давлениях. Найденное значение константы А может быть использовано для расчета теплоты испарения:

DН_исп.= R × A (1.72)

В соответствии с эмпирическим правиломТрутона мольная теплота испарения неполярных жидкостей (Дж/моль) связана с их температурой кипения при атмосферном давлении Т^о_кип ( К) соотношением:

. (1.73)

Это соотношение может быть использовано для расчета теплоты испарения неполярных жидкостей:

DH_исп.=89,12 × Т^о_{кип .}.(1.74)

Сопоставление найденных на основе экспериментальных данных значений теплот испарений с рассчитанными значениями DH_исп по правилу Трутона для данных жидкостей позволяет оценивать их полярность.

П р и м е р 1.21. Зависимость давления пара (мм рт. ст.) от температуры для жидкого металлического цинка выражается уравнением

Вычислить теплоту испарения цинка при температуре плавления (692,7 К).

Р е ш е н и е

Теплоту испарения цинка при температуре 692,7 К рассчитываем по уравнению (1.66), в котором ΔH_ф.п. = ΔH_исп.. Уравнение преобразуем к следующему виду:

Дифференцируя приведенное в условии задачи уравнение зависимости давления пара жидкого металлического цинка от температуры, получаем:

Подставляя полученное выражение в формулу для расчета теплоты испарения, получим:

П р и м е р 1.22. Температура кипения метилового спирта равна 34,7 ^оС при давлении 200 мм рт. ст. и 49,9 ^оС при давлении 400 мм рт. ст. Рассчитать теплоту испарения и температуру кипения метилового спирта при нормальном давлении (760 мм рт. ст.).

Запишем исходные данные, присваивая параметрам соответствующие индексы и переводя температуру в градусы по шкале Кельвина:

Т₁ = 34,7 + 273,2 = 307,9 К; P₁ = 200 мм рт. ст.;

Т₂ = 49,9 + 273,2 = 323,1 К; P₂ = 400 мм рт. ст;

Т₃ =? P₃ = 760 мм рт.ст.

Р е ш е н и е

Рассчитываем теплоту испарения по формуле (1.69) по известным температурам кипения Т₁ и Т₂ при соответствующих давлениях P₁ и P₂:

.

Для определения Т₃ найденное значение теплоты испарения, известную пару значений Т₁, P₁, а также величину P₃ подставляем в формулу (1.68):

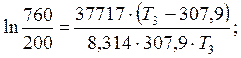
T₃ · ln 3,8 = 14,734 · (T₃ – 307,9);

1,335 Т₃ = 14,734 Т₃ – 4536,599; 13,399 · Т₃ = 4536,599;

T₃ = 338,58 K = 65,38 ^оС.

П р и м е р 1.23. При нормальном атмосферном давлении (P₁ = 101325 Па) гексан кипит при температуре 69 ^оС. Определить мольную теплоту испарения гексана и давление насыщенного пара этого вещества при температуре 25 ^оС.

Р е ш е н и е

Температура кипения гексана при нормальном атмосферном давлении Т₁ = 69 + 273,2 = 342,2 К. Т₂ = 25 + 273,2 = 298,2 К. P₂ =?

Гексан – неполярная жидкость, поэтому теплоту испарения рассчитываем, применяя правило Трутона, по формуле (1.74):

ΔH_исп. = 89,12 · 342,2 = 30497 Дж/моль.

Для нахождения P₂ найденное значение теплоты испарения, известную пару значений Т₁ и P₁, а также температуру Т₂ подставляем в уравнение (1.68):

П р и м е р 1.24. Температура кипения бензола при давлении 1 атм равна 80,1 ^оС. Теплота испарения бензола составляет 31,1 кДж/моль. Чему равно давление насыщенного пара бензола при 25 ^оС?

Р е ш е н и е

Запишем исходные данные, присваивая параметрам соответствующие индексы и переводя температуру в градусы по шкале Кельвина:

Т₁ = 80,1 + 273,2 = 353,3 К; P₁ = 1 атм;

Т₂ = 25 + 273,2 = 298,2 К; P₂ =?

Подставим известные величины в уравнение (1.68), при этом теплота испарения должна быть выражена в Дж/моль:

P₂ = e^–1,956 = 0,141 атм.

Растворами называются гомогенные системы, состоящие из двух и более компонентов, состав которых в определенных пределах может непрерывно изменяться. Различают газообразные, жидкие и твердые растворы. Растворы бывают идеальные (разбавленные и совершенные) и реальные. Состав растворов задается качественно и количественно.

Дата добавления: 2017-01-14