Термодинамические потенциалы

Р е ш е н и е

Р е ш е н и е

Р е ш е н и е

Р е ш е н и е

Р е ш е н и е

Т₁ = 25 + 273 = 298 К; Т₂ = 600 + 273 + 873 К.

Расчет производим, подставив в формулу (1.32) уравнение зависимости теплоемкости алюминия от температуры:

П р и м е р 1.9. Рассчитать изменение энтропии при нагревании 1 кг монооксида углерода от температуры 300 К (Т₁) до температуры 600 К (Т₂), используя среднюю теплоемкость данного вещества в указанном интервале температур, а также с учетом зависимости его теплоемкости от температуры. Необходимые справочные данные о теплоемкостях монооксида углерода приведены в табл. 1.1.

Находим количество молей нагреваемого монооксида углерода (СО):

n = g /M = 1·10³/28 = 35,71 молей,

где g – масса диоксида углерода, в г; M = 28 г/моль – молярная масса СО;

Изменение энтропии при нагревании 1 кг газообразного монооксида углерода от температуры 300 К (Т₁) до температуры 600 К (Т₂), если для расчета используется средняя теплоемкость данного вещества в интервале температур 298-600, рассчитываем по уравнению (1.33):

ΔS =35,71·29,99· ln 600/300 = 742,32 Дж/К.

Точный расчет производим, подставив в формулу (1.32) уравнение зависимости теплоемкости СО от температуры (C_P = 28,41 + 4,10· 10^-3 Т – 0,46· 10⁵/ T²):

= 35,71(19,688 + 1,230 – 0,192) = 740,13 Дж/К.

П р и м е р 1.10. Рассчитать изменение энтропии при расширении 100 г водорода в вакууме при постоянной температуре, если его объем увеличился в 3 раза.

Так как расширение газа совершается при постоянной температуре, то применим уравнение (1.34):

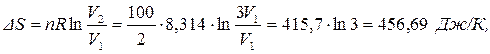
где 2 – молярная масса водорода, г/моль; V₁ – начальный объем водорода.

П р и м е р 1.11. Рассчитать изменение энтропии при плавлении 0,5 молей льда при температуре 0 ^оС (273 К), если теплота плавления ΔH_пл = 6025 Дж/моль.

Расчет изменения энтропии при фазовом переходе производим по формуле (1.36) с учетом количества молей (n) плавящегося вещества:

.

П р и м е р 1.12. Рассчитать изменение энтропии при нагревании 0,7 моль моноклинной серы от 25 ^оС (298 К) до 200 ^оС (473 К) при давлении 1 атм, если мольные теплоемкости серы (Дж·моль^-1·К^-1) равны: С_P(S_тв) = 23,64; C_P (S_ж) = 35,73 + 1,17 ·10^-3 Т; мольная теплота плавления моноклинной серы ΔH_пл = 1446,4 Дж/моль, температура плавления моноклинной серы 119 ^оС (392 К).

Общее изменение энтропии складывается из изменений энтропий на трех стадиях: 1) при нагревании твердой серы от 298 до температуры плавления 392 К в твердом состоянии (ΔS₁); 2) при плавлении серы при температуре 392 К (ΔS₂); 3) при нагревании жидкой серы от 392 до 473 К (ΔS₃):

ΔS = ΔS₁ + ΔS₂ + ΔS₃.

Для одного моля моноклинной серы:

Для 0,7 молей моноклинной серы изменение энтропии составит:

ΔS = 16,977 · 0,7 = 11,88 Дж· К^-1.

П р и м е р 1.13. Рассчитать изменение энтропии при превращении 1 моля льда, взятого при 0 ^оС (273 К), в пар при температуре 100 ^оС (373 К). Теплота плавления льда ΔH_пл = 6025 Дж/моль, теплота испарения воды ΔH_исп = 40590 Дж/моль, теплоемкость жидкой воды 75,44 Дж/моль·К.

Р е ш е н и е

Общее изменение энтропии складывается из изменений энтропий на трех стадиях: 1) при плавлении льда при температуре 273 К (ΔS₁); 2) при нагревании воды от 273 К до 373 К в жидком состоянии (ΔS₂); 3) при испарении воды при температуре 373 К (ΔS₃):

ΔS = ΔS₁ + ΔS₂ + ΔS₃.

1.5.2. Расчет изменений энтропии химических реакций

На основе постулата Планка существует возможность расчета абсолютной энтропии, то есть энтропии, отсчитанной от нулевого значения при Т = 0. Если вещество при изменении температуры от 0 К до Т К претерпело ряд фазовых переходов и стадий нагревания в различных фазовых состояниях при P = const, то, основываясь на вышеизложенном (глава 1.2.1), абсолютная энтропия газообразного вещества при температуре Т может быть рассчитана по следующему уравнению:

(1.37)

В справочных термодинамических таблицах приведены рассчитанные значения абсолютной энтропии веществ в стандартном состоянии – при температуре 298 К и стандартном давлении . С использованием этих значений может быть рассчитано стандартное изменение энтропии химических реакций, которое равно разности абсолютных энтропий продуктов реакции и абсолютных энтропий исходных веществ с учетом стехиометрических коэффициентов (количества молей):

(1.38)

Изменение энтропии химических реакций при нестандартной температуре при отсутствии фазовых переходов рассчитывают с учетом зависимости :

(1.39)

где ΔС_P – разность изобарных теплоемкостей продуктов реакции и исходных веществ с учетом количества молей реагентов (стехиометрических коэффициентов).

В точных расчетах необходимо учитывать зависимость ΔС_Р = f(T):

ΔС_P = Δa + Δb·T + Δc ·T² + Δc΄/ T².

Тогда после интегрирования получим:

(1.40)

П р и м е р 1.14. Рассчитать стандартное изменение энтропии и изменение энтропии при Т = 500 К реакции, проходящей в газовой фазе:

CH₃OH +1,5 O₂ = CO₂ + 2 H₂O.

метанол СH₄O

Необходимые справочные данные представлены в табл. 1.8.

Таблица 1.8

Абсолютные энтропии и коэффициенты в уравнениях С_P = f(T)

Вещества	Коли- чество молей νi	, Дж/моль∙K	Коэффициенты в уравнениях СP = f(T)
a	b·10 ^3	c·10 ^6	c΄·10^–5
CH3OH		239,76	15,28	105,20	–31,04	–
O2	1,5	205,04	31,46	3,39	–	–3,77
CO2		213,66	44,14	9,04	–	–8,54
H2O		188,72	30,00	10,71	–	0,33

Стандартное изменение энтропии находим по формуле (1.38):

Для данной химической реакции находим значения коэффициентов Δa, Δb, Δc, Δc ΄ уравнения ΔС_P = f(T):

Δa = (44,14 + 2 · 30,00) – (15,28 + 1,5 · 31,46) = 41,67;

Δb = {(9,04 + 2 ·10,71) – (105,20 + 1,5 · 3,39)} · 10^-3 = –79,82 · 10^–3;

Δc = – (–31,04) · 10^–6 = 31,04 · 10^–6;

Δc΄ = {(–8,54 + 2 · 0,33) – 1,5 · (–3,77)} · 10⁵ = –2,22· 10⁵.

Уравнение зависимости изменения теплоемкости от температуры после подстановки в него значений Δa, Δb, Δc, Δc ΄ будет иметь вид:

ΔС_P = 41,67 – 79,82 · 10^-3 Т + 31,04 · 10^-6 T² –2,22· 10⁵/ T².

Для нахождения изменения энтропии данной химической реакции при температуре 500 К найденные значение ΔS^о₂₉₈ и уравнение ΔС_P = f(T) подставляем в формулу (1.39):

1.5.3. Определение возможности самопроизвольного протекания химических процессов. Расчет изменения энергии Гиббса и изменения энергии Гельмгольца.

Самопроизвольные химические реакции, являясь разновидностью самопроизвольных термодинамических процессов, согласно второму закону термодинамики сопровождаются убылью свободной энергии системы и заканчиваются установлением в системе химического равновесия. В неизолированных (открытых) системах возможность протекания самопроизвольных процессов, их направленность и условия наступления равновесия при соответствующих внешних параметрах определяются с помощью термодинамических потенциалов (табл. 1.9).

Таблица 1.9

Термодина- мический потенциал	Постоянные величины	Условия самопроизвольного протекания процесса	Условия равновесия
U	S = const, V = const	d U < 0	d U = 0, d^2 U >0
H	S = const, P = const	d H < 0	d H = 0, d^2 H >0
F	T = const, V = const	d F < 0	d F = 0, d^2 F >0
G	T = const, P = const	d G < 0	dG = 0, d^2 G >0

Наибольшее значение в конкретных термодинамических расчетах имеют энергия Гиббса G (при P = const и T = const – изобарно-изотермический потенциал) и энергия Гельмгольца F (при V = const и T = const – изохорно-изотермический потенциал). Уменьшение энергии Гиббса и энергии Гельмгольца равно максимальной работе, которую может совершить система в соответствующем процессе. При самопроизвольных процессах G и F всегда уменьшаются (dG < 0 и dF < 0, соответственно), а в состоянии равновесия они достигают минимального значения и не изменяются. Условия равновесия при постоянстве соответствующих параметров:

dG = 0 (P, T = const); dF = 0 (V,T = const). (1.41)

Большинство химических и металлургических процеccов происходит при Р = const и T = const. Поэтому ниже рассматриваются методы расчета изменения энергии Гиббса (ΔG) химических реакций. Для того, чтобы рассчитать изменение энергии Гельмгольца (ΔF) при температуре Т, необходимо воспользоваться следующим соотношением:

ΔF = ΔG – Δn · RT, (1.42)

где Δn – изменений числа молей газообразных веществ за счет прохождения химической реакции; R = 8,314 Дж/(моль·К) – универсальная газовая постоянная.

Дата добавления: 2017-01-14