Порядок выполнения практической части.

Исходные данные (задаются преподавателем).

5.1. Контролируемый параметр (d_g=14мм).

5.2. Допуск IT на изготовление детали.

5.3. Схема измерения (4 измерения каждой детали – в 2^х продольных и 2^х поперечных сечениях.

5.4. Закон распределения случайных погрешностей.

5.5. Объем N общей выборки – 50 деталей.

5.6. Объем n мгновенной выборки – 5 деталей.

5.7. Центр X_H настройки верхний предельный размер или ось симметрии поля допуска детали.

6.1. Образуйте общую выборку, расположив детали, подлежащие измерению, в порядке, в котором они обрабатывались.

6.2. Образуйте m=N-n+1 мгновенных выборок заданного объема.

6.3. Настройте микрокатор, установленный в измерительной стойке, на размер, используя концевые меры длины.

6.4. Измерьте каждую деталь в заданных сечениях и направлениях, результаты измерений занесите в протокол № 1отчета (табл. 8.1)

Таблица 8.1 – Результаты измерения деталей.

№ детали n/n	Действительные отклонения в сечениях, мкм	Расчет отклонений формы, мкм	Размер детали, мм
1А	1Б	2А	2Б	В поперечном сечении	В продольном сечении

6.5. Определите по формуле (8.2) средние значения X_j (1≤j≤m) контролируемого параметра для каждой мгновенной выборки. Результаты занесите в протокол № 2.

6.6. Определите значение систематической погрешности δ_c по формуле:

_ _

δ_c = Х_m – Х_1, (8.4)

где 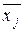, 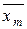- средние значения контролируемого параметра, определенные соответственно по первой и последней мгновенным выборкам.

6.7. Постройте график 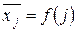и, ориентируясь на данные приложения 1, выдвиньте гипотезу о виде аппроксимирующей его функции.

Предположим, что аппроксимирующая функция линейна, т. е. имеет вид:

(8.5)

В этом случае:

1) заполните колонки 3 и 4 протокола №2 отчета;

2) вычислите коэффициенты 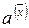и 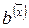по формулам:

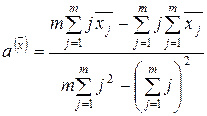, (8.6)

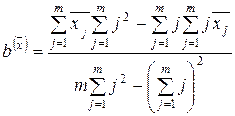. (8.7)

3) подставьте значения 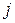, , 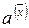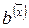в уравнение (8.5) и определите выравненные значения 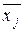по каждой выборке; заполните окончательно протокол №2 отчета;

4) рассчитайте основную погрешность 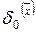определения 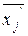по формуле:

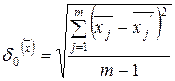. (8.8)

В случае нелинейности аппроксимирующей функции методика, изложенная в настоящем пункте, в принципе сохраняется (изменяются графы протокола №2 в соответствии с изменением формул для определения коэффициентов функциональной зависимости).

6.8. Определите с помощью формулы (4.2) средние квадратические отклонения по каждой мгновенной выборке. Заполните колонки 1. и 2 протокола №3 отчета.

6.9. Определите случайную погрешность 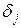обработки деталей по каждой выборке, имея в виду, что мгновенное поле рассеяния должно охватывать 99,73% всех значений контролируемого параметра. При нормальном распределении мгновенного поля рассеяние . Занесите результаты определения 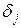в колонку 3 протокола №3 отчета.

6.10. Постройте график 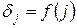и, ориентируясь на данные приложения 1, выдвиньте гипотезу о виде аппроксимирующей его функции. В случае линейности аппроксимирующей функции: 1) заполните колонки 4 и 5 протокола №3 отчета; 2) вычислите коэффициенты 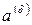и 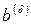по формулам:

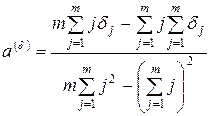, (8.9)

. (8.10)

3) Определите 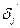подставляя в уравнение:

, (8.11)

Значения 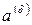, , 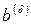, 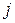выравненные значения 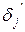, заполните окончательно протокол №3 и вычислите основную погрешность определения по формуле:

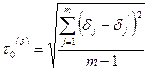. (8.12)

В случае нелинейности аппроксимирующей функции методика, изложенная в настоящем пункте, в принципе сохраняется (изменяются графы протокола и формулы для определения коэффициентов функциональной зависимости).

6.11. Определите числовое значение выражения 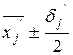по последней мгновенной выборке и оцените с его помощью соответствие исследуемого технологического процесса требованиям технологической документации.

Дата добавления: 2017-02-01