Застосування тригонометричних рядів до розвзування задач математичної фізики.

Розділ II.

У багатьох задачах науки і техніки часто як математичні моделі певних процесів виступають тригонометричні ряди Фур’є. Проте застосування таких рядів у задачах моделювання має певні особливості. Так, зокрема, зрозуміло, що в більшості випадків на практиці інтерес становлять лише моделі, які подаються рівномірно збіжними рядами Фур’є.

Так ряди Фур’є лежать в основі одного з найважливіших методів розв’язання крайових задач математичної фізики - метод відокремлення змінних ( метод стоячих хвиль або метод Фур ` є). Це один з найбільш ефективних аналітичних способів розв`язання крайових задач для широкого кола лінійних ДРЧП. Звичайно його застосовують тоді, коли рівняння і граничні умови є лінійними та однорідними. У багатьох випадках він дозволяє будувати розв`язки крайових задач і для неоднорідних ДРЧП з неоднорідними граничними умовами. Метод відокремлених змінних для диференціальних рівнянь з частинними похідними зводяться до задачі Штурма-Ліувілля для функції від однієї незалежної змінної.

2.1. Задача Штурма - Ліувілля.

Нехай задано диференціальний оператор

на відрізку , причому і неперервно диференційовна на цьому проміжку, –неперервна на цьому ж проміжку. Від функції вимагаємо, щоб вона була

а) двічі неперервно диференційовною на ;

б) неперервно диференційовною на ;

в) справджувала крайові умови

де – сталі, 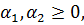, – додатна, неперервна на ; функція, яка називається ваговою.

Задачею Штурма-Ліувілля [3, 5] називають задачу знаходження таких значень (власних значень задачі Штурма-Ліувілля), для яких рівняння

має ненульовий розв’язок (власну функцію задачі Штурма-Ліувілля, яка відповідає даному власному значенню).

Для розв’язків задачі Штурма-Ліувілля мають місце наступні властивості:

1. Всі власні значення дійсні, невід’ємні при , їх множина зліченна, тобто може бути упорядкована:

2. Кожному власному значенню відповідає одна власна функція.

3. Власні функції, що відповідають різним власним числам, ортогональні на з вагою , тобто при

де – власні функції, які відповідають власним значенням

4. Справедлива теорема Стеклова: Власні функції утворюють базис у просторі двічі неперервно диференційовних на функцій 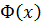, які справджують крайові умови, тобто кожна така функція є сумою рівномірно та абсолютно збіжного ряду Фур’є:

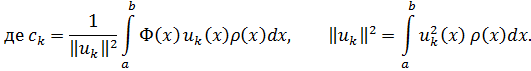
5. Якщо то відповідний ряд Фур’є збігається до 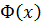у середньому з вагою , тобто

Дата добавления: 2017-02-01