Застосування методу відокремлених змінних до розв’язуваняння рівнянь параболічного типу типу

При дослідженні фізичних процесів різної природи часто зустрічаються ДРЧП параболічного типу. Так, наприклад, рівнянням

описуються такі процеси:

а) поширення тепла в однорідному ізотропному тілі. Тоді є температура точок тіла в різні моменти часу, – коефіцієнт внутрішньої теплопровідності тіла, c - його питома теплоємність, ρ – густина), , де F(t,x,y,z) – інтенсивність внутрішніх джерел тепла;

б) дифузія рідини або газу в однорідному середовищі. Тоді є концентрація речовини в точках середовища в різні моменти часу, (d – коефіцієнт дифузії, c – коефіцієнт пористості середовища), 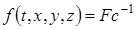, де F(t,x,y,z) – інтенсивність внутрішніх джерел речовини.

При складанні математичних моделей фізичних процесів, які відбуваються в об’єктах скінчених або напівнескінчених розмірів, окрім рівняння та початкової умови необхідно задавати режими на краї об’єкта (крайові умови), що приводить до змішаних задач для ДРЧП.

Для прикладу розглянемо наступну задачу: Дослідити процес теплоти в однорідному стержні завдовжки із теплоізольованою бічною поверхнею, якщо його початкова температура дорівнює , а на кінцях підтримується нульова температура.

Зі сформованої задачі випливає, що необхідно знайти розв’язок диференціального рівняння в області

Яякий задовольняє початкові умови

і крайові

Вважаємо, що функція задовольняє умови узгодженості

Будемо шукати розвязок мішаної задачі (2.91) – (2.93) у вигляді

Підставивши (2.95) у рівняння (2.91) і крайові умови (2.93) та відокремивши змінні, дістанемо

де – довільна стала.

Власними значеннями задачі Штурма-Ліувілля (2.97), (2.98) , а відповідно власні функції мають вигляд

Підставивши власні значення в рівняння (2.96) та зінтегрувавши його, дістанемо

Підставляючи (2.99) і (2.100) у (2.95), знаходимо

де – довільні сталі.

Отже, дістали нескінченну систему частинних розв’язків рівняння (2.91), які задовольняють крайові умови (2.93).

Згідно із доведеною лемою 2.1 ряд

також буде розв’язком рівняння (2.91), якщо він збігається і його можна почленно диференціювати один раз за і двічі за , причому цей ряд задовольняє і крайові умови (2.93).

Припустимо, що умови (2.93) виконуються. Тоді для відшукання єдиного розв’язку мішаної задачі (2.91) – (2.93) залишило вибрати коефіцієнти таким чином, щоб ряд (2.101) задовольняв і початкову умову, тобто щоб

Нехай функція , де – клас неперервних функцій, які мають кусково-неперервну похідну при і задовольняють умови узгодженості (2.94). Тоді на відрізку функція розвивається в ряд Фур’є за системою власних функцій і з рівності (2.102) маємо

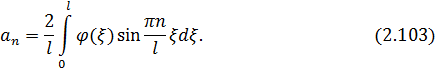
Підставивши знайдені коефіцієнти (2.103) у ряд (2.101), дістанемо формальний розв’язок мішаної задачі (2.91) – (2.93).

Для обґрунтування добутого результату доведемо таке твердження.

Твердження 1. Якщо , то ряд (2.101), де коефієнти визначаються формулою (2.103), в області можнапочленно диференціювати довільну кількість разів як , так і за , причому він визначає неперервну функцію в .

Доведення

За умовою твердження при маємо

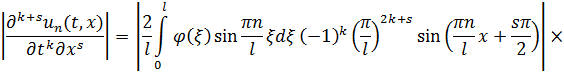
Де при .

Оскільки

то згідно з ознакою Д’Аламбера ряд збігається, а отже, на підставі (2.104) ряди

збігаються рівномірно при .

При справедлива оцінка

Але якщо , то з теорії рядів Фур’є відомо, що ряд збігається, а отже ряд (2.101) в області збігається рівномірно, й твердження доведенно.

Підставивши (2.103) у (2.101), дістанемо

Оскільки ряд

при збігається рівномірно, то порядок підсумування й інтегрування в попередній рівності можна змінювати, а отже,

Функція (2.105) називається функцією Гріна першої мішаної задачі для рівняння теплопровідності (2.91).

Дата добавления: 2017-02-01