Крайові задачі для рівняння коливань мембрани

Дослідимо коливання однорідної прямокутної мембрани зі сторонами і , які відбуваються внаслідок початкового відхилення, початкової швидкості і дії масової сили. Край мембрани нерухомо закріплений

Для визначення функції – відхилення мембрани від положення рівноваги маємо рівняння

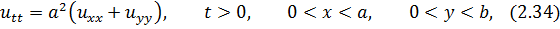
який задовольняє початкові умови

і крайові

Для побудови розв’язку мішаної задачі (2.34) – (2.37) розв’яжемо спочатку допоміжну задачу: знайти нетривіальні розв’язки рівняння (2.34), які задовольняли б крайові умови (2.36), (2.37).

Шукаємо ці розв’язки у вигляді

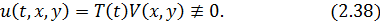
Підставивши (2.38) у рівняння (2.34) та крайові умови (2.36), (2.37) і відокремивши змінні, дістанемо

Перше з рівнянь системи (2.40) називається Гельмгольца.

Задачу на власні значення (2.40) для диференціального рівняння з частинними похідними другого порядку також розв’язуємо методом відокремлення змінних. Візьмемо

Відокремлюючи змінні в задачі (2.40), дістанемо

Повторюючи міркування, викладені в дослідженні задачі Штурма-Ліувілля (2.7), (2.8), матимемо

Отже, згідно з (2.41) власним значенням задачі (2.41)

відповідатимуть власні функції

де – деякий сталий множник. Виберемо його таким чином, щоб норма власної функції із вагою 1 дорівнювала одиниці, тобто

З останньої рівності знаходимо .

Ортогональність функцій у розглядуваному прямокутнику очевидна й не вимагає доведення.

Отже, система функцій

є ортонормованою системою власних функцій прямокутної мембрани.

Зазначимо, що серед знайдених власних значень можуть бути й кратні, тобто такі, яким відповідає не одна, а кілька лінійно незалежних власних функцій. Кількість лінійно незалежних власних функцій, які відповідають власному значенню , залежить від кількості цілочислових розв’язків і рівняння

Наприклад, якщо , то власному значенню відповідатимуть дві лінійно незалежні функції

тобто є двократним власним значенням.

Нехай – довільна задана в прямокутнику дійсна інтегрована з квадратом функція

коефіцієнтами Фур’є функції відносно ортономованої системи (2.44)

називається середньою квадратичною похибкою. Маємо

Таким чином, середня квадратична похибка за фіксованих і буде мінімальною при .

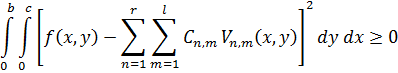
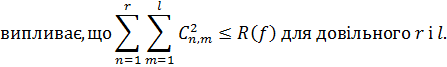
Отже, ряд складений із квадратів коефіцієнтів Фур’є функцій збігаються:

Добуте співвідношення називається нерівність Бесселя.

Означення. Ортонормавану систему функцій у прямокутнику [0,b;0,c] називають повною, якщо для всякої неперервної і інтегрованої з квадратом у цьому прямокутникові функції справедлива рівність Парсевалля-Стеклова

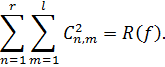
Твердження. Власні функції і , які відповідають різним значенням задаці (2.40), є ортогональними

Припустимо тепер, що задача (2.40) має власну функцію яка не належить системі (2.44). згідно з наведеного твердження вона є ортогональною до всіх функцій (2.44). із теорії кратних рядів Фур’є відомо: якщо функція і задовольняє крайові умови задачі (2.40), то її можна розвинути в абсолютно й рівномірно збіжний ряж за системою власних функцій (2.44). Унаслідок ортогональності і у розвиненні функції за системою (2.44) залежить тільки скінченне число членів, які відповідають власному значенню Тому є лінійною комбінацією лише тих функцій (2.44), які відповідатимуть власному значенню . Отже, всі власні функції прямокутної мембрани даються формолою (2.44).

Підставивши знайдені власні значення у рівняння (2.39) і зінтегрувавши його, дістанемо

де , – довільні сталі. Підставляючи (2.44) і у рівняння (2.38), маємо

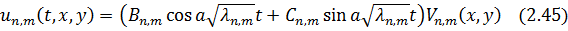
Ми дістали нескінченну множину частинних розв’язків лінійного однорідного рівняння (2.34), які задовольняють крайові умови (2.36), (2.37).

Згідно з доведеної леми [] ряд

також буде розв’язком рівняння (2.34) і задовольняє крайові умови (2.36), (2.37), якщо він збігається рівномірно і його можна почленно диференціювати двічі за у розглядуваній області

Визначимо коефіцієнти і таким чином, щоб ряд (2.46) задовольняв і початкові умови (2.35). Для цього підставляємо (2.46) у (2.34):

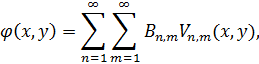
(2.47)

Припустимо, що ряди (2.47) збігаються рівномірно в прямокутнику . Тоді, помноживши їх на функцію та зінтегрувавши добутий результат по прямокутнику, матимемо

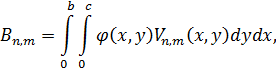
Підставивши знайдені значення і у ряд (2.46), дістанемо розв’язок мішаної задачі (2.34) – (2.37).

Обґрунтування методу відокремлення змінних.

Теорема. Якщо функцій та неперервні разом із похідними до четвертого порядку включно в прямокутник то ряд (2.46) збігається рівномірно в області і його можна почленно диференціювати двічі за і .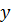

Доведення

Унаслідок крайових умов

Беручи до уваги та інтегруючи частинами, дістанемо

Очевидно, існує така стала , що

а отже, останній збігається абсолютно й рівномірно в області .

Здиференціюємо почленно ряд (2.46) двічі за і . Маємо

Унаслідок (2.48) мажорантними для рядів (2.49) будуть числові ряди

які є збіжними. Але тоді (2.49) абсолютно й рівномірно збіжні в області .

Теорему доведено.

Зазначимо, що твердження є справедливими і тоді, коли

2.3. Загальна схема методу відокремлення змінних

Метод Фур'є побудови розв'язку мішаної задачі можна застосувати лише для певного класу лінійних ДРЧП другого порядку. У зв'язку з дим розглянемо диференціальне рівняння

де коефіцієнти – досить гладкі функції при 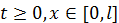і

На підставі останніх умов рівняння (2.50) належить до гіперболічного типу.

Нехай потрібно знайти розв'язок рівняння (2.50) при , який задовольняв би початкові умови

і крайові

де сталі такі, що

Формальна схема методу відокремлення змінних. Побудову розв'язку мішаної задачі (2.50)—(2.52) розіб'ємо на два етапи.

Перший етап. Шукаємо нетривіальні розв'язки рівняння (2.50), які задовольняли б крайові умови (2.52), у вигляді

Підставивши (2.53) у рівняння (2.50), крайові умови (2.52) та розділивши змінні, дістанемо

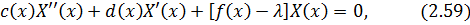
де – довільна стала.

Таким чином, ми прийшли до задачі Штурма-Ліувілля: дістати ті значення параметра (власні значення), за яких задача (2.59), (2.50) має нетривіальні розв'язки (власні функції), і знайти ці розв'язки.

Сукупність усіх власних значень задачі (2.59), (2.60) називається її спектром.

Припустимо, що задачу Штурма-Ліувілля (2.59), (2.60) розв'язано і – її власні значення, а – відповідні власні функції.

Унаслідок однорідності рівняння (2.59) і крайових умов (2.60) власні функції визначаються з точністю до сталого множника. Але всякому власному значенню задачі (2.59), (2.60) відповідає тільки одна лінійно незалежна власна функція. (В цьому випадкові кажуть, що власні значення розглядуваної задачі Штурма-Ліувілля є простими.) Справді, якщо власному значенню відповідали б дві лінійно незалежні власні функції і , то функція

була б загальним розв'язком рівняння (2.59) при , який задовольняє крайові умови (2.60). Але це неможливо, бо завжди можна знайти розв'язок рівняння (2.59) за таких початкових умов і , що він не задовольнятиме першу з крайових умов (2.60) (наприклад, поклавши .

Покажемо, що рівняння (2.59) можна подати у вигляді

де - цілком визначена для заданого рівняння функція. Справді, домноживши (2.59) на , дістанемо

Виберемо таким чином, щоб

Маємо

Введемо позначення: . Тоді внаслідок (2.62) рівняння (2.61а) запишеться у вигляді (2.61). ^\

Оскільки власні функції визначаються з точністю до сталого множника, то виберемо його таким чином, щоб

Власні функції, які задовольняють умову (2.63), називаються нормованими.

Всяка власна функція , помножена на число стає нормованою. Очевидно, що кожному власному значенню задачі Штурма-Ліувілля (2.59), (2.60) відповідає нормована власна функція, яка визначається з точністю до знака.

Теорема 1. Якщо – два різних власних значення задачі Штурма-Ліувілля (2.59), (2.60), то відповідні їм власні функції і ортогональні з вагою на відрізку , тобто

З умови ортогональності власних функцій випливає дійсність власних значень. Справді, якщо існує комплексне власне значення , якому відповідає комплексна власна функція , то на підставі того, що коефіцієнти рівняння (2.59) і крайових умов (2.60) є дійсними, комплексно-спряжене число також буде власним значенням і йому відповідатиме комплексно-спряжена з власна функція . З умови ортогональності маємо

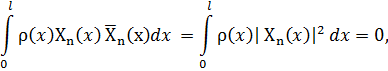
тобто , а це означає, що комплексне число не є власним значенням.

Теорема 2. Якщо існують власні значення задачі Штурма-Ліувілпя (2.59), (2.209), де , то вони додатні.

Зазначимо, що власні функції задачі (2.59), (2.60) створюють повну систему, тобто не існує ненульової квадратно сумовної функції, яка була б ортогональною до всіх власних функцій.

Переходимо до інтегрування рівняння (2.58). Підставивши в нього власне значення знаходимо два його частинних розв'язки і , які задовольняли б умови

Очевидно, розв'язки і , є лінійно незалежними, а отже, загальний розв'язок рівняння (2.58) можна записати у вигляді

це , — довільні сталі.

Згідно з (2.53) маємо

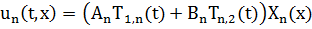
Функції за будь-яких задовольняють рівняння (2.50) і крайові умови (2.53).

Другий етап. За допомогою знайдених нетривіальних розв'язків будуємо розв'язок поставленої мішаної задачі (2.50)-(2.52).

Розглянемо ряд

і припустимо, що при , він збігається рівномірно і його можна почленно диференціювати двічі за двічі за . Тоді ряд (2.65) буде розв'язком рівняння (2.50) через його лінійність та однорідність і задовольнятиме крайові умови (2.52).

Підставивши (2.65) у початкові умови (2.51) і врахувавши (2.64), дістанемо

Помножимо добуті рівності на і зінтегруємо їх за у межах від 0 до . Тоді, врахувавши ортонормованість власних функцій, матимемо

Підставивши знайдені коефіцієнти , у ряд (2.65), дістанемо розв’язок мішаної задачі (2.203)-(2.205)

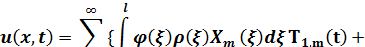
Обґрунтування методу Фур’є

Для цього необхідно показати:

· Існування розв’язків задачі Штурма-Ліувілля;

· Можливість розвинення функцій і на відрізку у ряди за системою власних функцій задачі Штурма-Ліувілля (2.59), (2.60).

· Рівномірно збіжність рядів (2.66) при і його почленну диференційованість двічі за t і двічі за x.

Для доведення існування розв’язку задачі Штурма-Ліувілля (2.59), (2.60) зведемо її до інтегрального рівняння. Для цього розглянемо функцію Гріна задачі (2.59), (2.60)

Означення 1. Функцією Гріна задачі (2.59), (2,60) називають функцію , визначену в квадратурах , яка задовольняє такі умови:

1) як функція від неперервна, а при має неперервні похідні за до другого порядку включно й задовольняє однорідне рівняння

2) як функція від задовольняє крайові умови (2.60);

3) Похідна першого порядку 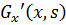при 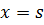зазнає розриву першого роду й має скачок, що дорівнює , тобто

Для спрощення наступних викладок вважатимемо, що в крайових умовах (2.209)

Будуємо функцію Гріна у вигляді

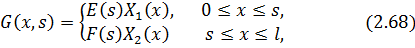
де , – довільні функції, визначені на , а , – два нетривіальних частинних розв’язків рівняння (2.67), які задовольняють умови

Розв’язки , існують і є лінійно незалежними. Справді якщо б , то згідно умови (2.69) ми би мали

тобто було б власне значенням задачі Штурма-Ліувілля (2.59), (2.60), а це суперечить теоремі 2.6 про додатність власних значень.

З умови неперервності функції Гріна в прямокутнику , маємо

тобто

Визначивши з цього відношення функції і та підставивши їх у (2.68), дістанемо функцію

яка задовольняє першу й другу умови функції Гріна. Згідно третьою умовою маємо

Тобто

Вираз у квадратних дужках є детермінантом Вронського лінійно незалежних розв’язків рівняння (2.67) і згідно з відомого з курсу звичайних диференціальних рівнянь формулою Ліувілля

де – стала величина.

Таким чином, і шукана функція Гріна має вигляд

Із (2.70) випливає симетричність функції Гріна, тобто

Теорема 1. Задачі Штурма-Ліувілля (2.61), (2.60) та інтегральне рівняння

еквівалентні.

Введемо позначення

Тоді, помноживши рівняння (2.71) на дістанемо

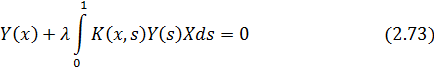
Отже, задача Штурма-Ліувілля (2.61), (2.60) еквівалентні інтегральному рівнянню Фредгольма другого роду з дійсними систематичним ядром .

Для інтегрального рівняння (2.73) справедливі наступні теореми.

Теорема 2. Інтегральне рівняння (2.72) з дійсним симетричним ядром, яке не дорівнює тотожно нулю, має принаймні одне власне значення.

Теорема 3. Усі власні значення рівняння (2.73) із симетричним ядром є дійсними числами.

Теорема 4. Усі власні функції інтегрального рівняння з дійсними симетричними ядрами є дійсними.

Отже, на підставі еквівалентності інтегрального рівняння (2.73) і задачі Штурма-Ліувілля (2.61), (2.60) можемо стверджувати:

1) розв’язок задачі Штурма-Ліувілля (2.61), (2.60) існує;

2) власні значення є дійсними числами, а власні функції – дійсними функціями.

Наведемо достатні умови розвинення на проміжку функції та у рівномірно збіжні ряди за системою власних функцій задачі Штурма-Ліувілля (2.61), (2.60). Для цього наведемо наступну теорему

Теорема 5. (СТЕКЛОВА): Нехай – довільна з класу функція, яка задовольняє умови

Тоді на відрізку розвивається в рівномірно й абсолютно збіжний ряд за системою власних функцій 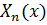задачі Штурма-Ліувілля (2.61).

На підставі цієї теореми можемо стверджувати: якщо і задовольняють умови узгодженості, то вони розвиваються в рівномірно збіжні ряди за системою власних функцій задачі (2.61), (2.60) на проміжку .

Для завершення обґрунтування методу відокремлення змінних покажемо, що ряд (2.66) збігається рівномірно при і що його можна почленно диференціювати двічі за та двічі за .

У подальшому вважатимемо що коефіцієнти рівняння (2.50) неперервні разом iз похідними до третього порядку включно в розглянуті області.

Введемо позначення

Теорема 6. Якщо функція і задовольняє умови

то ряд (2.66) збігається рівномірно і його можна почленно диференціювати двічі за і двічі за при

Доведення

Для спрощення наступних викладок покладемо

Тоді

і ряд (2.215) запишемо у вигляді

Для доведення рівномірної збіжності ряду (2.81) і рядів, які дістають унаслідок почленного диференціювання за і двічі за на проміжку , достатньо довести рівномірну збіжність таких рядів:

Оскільки внаслідок (2.61)

то з рівномірної збіжності рядів (2.82), (2.82а) випливає рівномірна збіжність ряду (2.82б)

Введемо позначення:

Лема: Нехай функція задовольняє умови і має на проміжку кусково-неперервну похідну, інтегровну з квадратом. Тоді справедлива нерівність

Доведення

Оскільки то . Інтегруючи частинами, маємо

Використовуючи цю рівності, дістанемо

Остання нерівність виконується для довільного , а отже, й при .

Лему доведено.

Функція 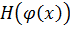задовольняє умови леми. Отже

Оскільки

то

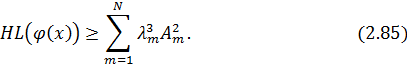
Маємо

Аналогічно

Відома нерівність Беcселя: для довільної нескінченної ортонормованої послідовності і довільної інтегрованої з квадратом функції на виконується нерівність

Беручи до уваги попередні рівності та нерівність Беселля, дістанемо

Рівність (2.74) еквівалентна рівності

звідки

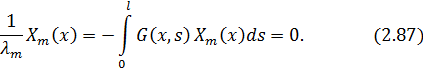
Таким чином зафіксованого є -м коефіцієнтом Фур’є функції яка задовольняє як функція умови доведеної леми. Тому

Диференціюючи (2.87) і застосовуючи нерівність Бесселя, дістанемо

Покажемо тепер, що ряд (2.87) рівномірно збіжний. Справді, застосовуючи нерівність Коші-Буняковського, маємо

Унаслідок нерівностей (2.85), (2.86) ряди 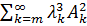, збіжні, а тоді з останьої нерівності випливає рівномірна збіжність ряду (2.82).

Беручи до уваги (2.89), дістанемо

Але

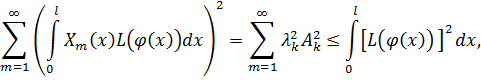
і, отже ряди 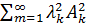, збіжні, Тоді з (2.90) випливає рівномірна збіжність при 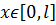ряду (2.82а).

Теорему доведено.

Дата добавления: 2017-02-01