Неоднорідне рівняння

Дослідити процес вимушених коливань однорідної струни задавши , нерухомо закріпленої на кінцях, якщо на неї діє рівномірно розподілена зовнішня сила інтенсивністю , а в початковий момент струна має форму і швидкість .

Для розв’язання поставленої задачі необхідно знайти розв’язок диференціального рівняння

Який задовольняє початкові умови

та крайові

Розв’язок мішаної задачі (2.19) – (2.21) шукатимемо у вигляді

де – розв’язок однорідного рівняння коливання струни, який задовольняє умови (2.19), (2.22); 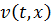– розв’язок рівняння (2.19) з однорідними початковими й крайовими умовами (2.21)

Згідно з формулою (2.12)

Функцію 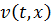шукаємо у вигляді

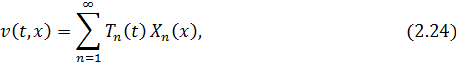
де – власні функції відповідної задачі Штурма-Ліувілля. В нашому випадкові (за різними крайовими умовами дістанемо різні власні функції).

Надалі вважатимемо, що ряд (2.24) збігається рівномірно і його можна почленно диференціювати двічі за і . Зазначимо, що ряд (2.24) задовольняє крайові умови. Залишилось функцію вибрати таким чином, щоб ряд (2.24) задовольняв рівняння (2.19) та однорідні початкові умови.

Нехай функцію можна розвинути в ряд Фур’є за системою власних функцій . Тоді матимемо

Підставивши (2.24) і (2.25) у рівняння (2.19), дістанемо

Остання рівність можлива тоді й лише тоді, коли

Для того щоб функція 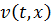задовольняла однорідні початкові умови, слід покласти

Інтегруючи задачі Коші (2.26), (2.27), дістанемо

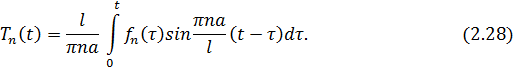
Підставивши (2.28) в (2.24), а потім добутий результат і (2.23) у (2.22), матимемо розв’язок поставленої мішаної задачі

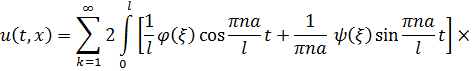
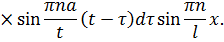
2.3.3. Задача про вимушені коливання струни з рухливими кінцями

Розглянемо вимушені коливання однорідної струни під дією зовнішньої сили, коли кінці струни не закріплені, а рухаються за заданим законом. Задача формулюється таким чином: знайти розв’язок u (x,t) неоднорідного хвильового рівняння

який задовольняє неоднорідні початкові умови

та неоднорідні крайові умови

Ідея розв’язання цієї задачі полягає в тім, щоб звести її до задачі з однорідними крайовими умовами, яку вже вміємо вирішувати для неоднорідного рівняння. З метою реалізації цієї ідеї візьмемо яку-небудь функцію , що задовольняє заданим крайовим умовам (2.31). Звичайно намагаються обрати цю функцію так, щоб вона була досить простою, але диференційованою. Легко зміркувати, що в розглянутому випадку функцію можна обрати у вигляді

Дійсно, тут

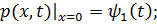
Тоді функція

буде задовольняти вже однорідним крайовим умовам. Відмітимо, що якщо крайові умови (2.31) будуть іншого виду, то й функцію потрібно підбирати в іншому вигляді.

Для функції що задовольняє однорідні крайові умови, складемо крайову задачу з огляду на задане диференціальне рівняння (2.29) і початкових умов (2.30). Для цього підставимо (2.33) у рівняння (2.29). Тоді отримаємо рівняння

або з урахуванням (2.32)

Знайдемо тепер початкові умови для :

Таким чином, отримаємо таку крайову задачу для функції знайти розв’язок неоднорідного рівняння

який задовольняє початкові умови

та однорідні крайові умови

Вирішивши цю задачу методом, викладеним раніше, і підставивши знайдене значення , визначимо шуканий розв’язок як суму .

Дата добавления: 2017-02-01