Застосуваняння методу відокремлених зміних до зозвязуваняння рівнянь еліптичного типу.

До рівнянь еліптичного типу приводить вивчення стаціонарних процесів різної фізичної природи (теплопровідність, дифузія, рівновага та інші). Одним із простіших рівнянь еліптичного типу є рівняння Лапласа

Крайові задачі для рівняння Лапласа у випадку прямокутних областей розв’язуються за допомогою методу відокремлення змінних (методу Фур’є) аналогічно до змішаних задач для рівнянь гіперболічного та параболічного типів.

Метод відокремлення змінних Фур'є, який було розглянуто В пункті 2.2 і 2.3, застосовується й до інтегрування задачі Діріхле у випадку таких простих областей, як круг, кільце, прямокутник і т. д. Тут методом Фур'є розв'яжемо задачу Діріхле для круга.

В крузі радіусом R із центром у початку координат знайти гармонічну функцію , яка на краю круга дорівнює , тобто в області знайти розв'язок рівняння Лапласа

який задовольняє крайову умову

У зв'язку з тим, що задача Діріхле (2.106), (2.107) може мати єдиний розв'язок, , і розв'язок мають бути періодичними з періодом 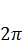функціями за .

Нетривіальні розв'язки рівняння (2.106) шукаємо у вигляді

Підставивши (2.108) у рівнянні Лапласа (2.106) та відокремивши змінні, дістанемо

де — довільна стала. Очевидно, .

Отже, потрібно знайти ті значення параметра , за яких рівняння (2.109) має ненульові періодичні з періодом 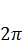розв'язки (власні значення) й побудувати ці розв'язки (власні функції). Легко бачити, що розв'язки рівняння (2.109), які відповідають двом різним власним значенням, ортогональні на відрізку 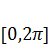. Покажемо, шо всі власні значення дійсні. Для цього припустимо супротивне: нехай є власним значенням, а відповідна йому власна функція буде .Тоді виконується тотожність

а отже,

Віднімаючи почленно ці тотожності, дістаємо

тобто власним значенням, а відповідна йому власна функція буде . Унаслідок ортогональності власних функцій має бути

Але

Отже, власні значення не можуть бути комплексними.

Нехай . Тоді (2.9) маємо . Для виконання умови періодичності потрібно покласти , і ми дістанемо

При ненульових періодичних розв'язків рівняння (2.109) не має. Нехай 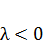. Тоді, зінтегрувавши (2.109), дістанемо загальний розв'язок який буде періодичним із періодом 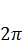, якщо .

Отже, ненульовими періодичними з періодом 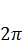розв'язками рівняння (2.109) будуть функції

Підставивши добуті значення у рівняння (2.110), матимемо

Рівняння (2.113) — це рівняння Ейлера, й підстановкою воно зводиться до вигляду

звідки

Або

Для того щоб функція (2.9) у крузі була неперервною, треба покласти Таким чином,

Підставляючи (2.112) і (2.115) у (2.108), дістаємо

де .

Унаслідок лінійності й однорідності рівняння Лапласа сума частинних розв’язків

також буде розв'язком рівняння Jlaiuiaca, якщо ряд (2.116) збігається рівномірно і його можна почленно диференціювати двічі за і в області . Припустимо, що ці умови виконуються. Тоді для визначення розв'язку задачі Діріхле (2.106), (2.107) залишилося так вибрати коефіцієнти і щоб ряд (2.116) задовольняв і крайову умову (2.107), на підставі якої

Ми дістали представлення функції 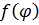на відрізку рядом Фур'є. З математичного аналізу відомо: якщо функція 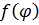періодична, неперервна й кусково-диференційовна на відрізку , то її ряд Фур'є в кожній точці збігається й має суму, що дорівнює 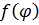, а коефіцієнти ряду визначаються за формулами

(2.117)

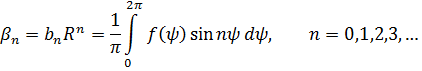
Підставивши знайдені коефіцієнти в ряд (2.116), дістанемо формальний розв’язок поставленої задачі Діріхле

Для обґрунтування добутого розв’язку доведемо наступну теорему.

Теорема: Якщо функція 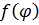періодична з періодом і неперервна на відрізку , то функція , визначена рядом (2.116), є гармонічною в крузі і неперервною в .

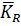Доведення

Спочатку припустимо, що 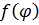є кусково-диференційовна на відрізку . Тоді, як відомо з теорії рядів Фур’є, ряд

збігається. Оскільки

то зі збіжності ряду (2.119) випливає рівномірна збіжність ряду (2.118) всюди в 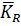, а отже, є неперервною в .

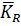Покажемо, що ряд (2.118) можна почленно диференціювати довільну кількість разів і за , і за при .

Здиференціюємо почленно (2.118) разів за . Маємо

Позначимо

і розглянемо рял

Для довільного

а отже, на підставі ознаки Д'Аламбера ряд (2.121) збігається при (унаслідок довільності ). Зі збіжності ряду (2.121) випливає рівномірна збіжність ряду (2.120), тобто ряд (2.118) можна почленно диференціювати довільну кількість разів за у крузі . Аналогічно доводиться можливість почленного диференціювання ряду (2.118) за у крузі .

Таким чином, якщо функція періодична з періодом 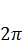, неперервна й кусково-диферендійовна, то ряд (2.118) є розв'язком задачі Діріхле (2.106), (2.107).

о

а

Доведемо тепер, що розв'язок задачі Діріхле (2.106), (2.107) представляється у вигляді ряду (2.118) й у випадку довільної неперервної функції 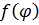. Для цього побудуємо послідовність неперервних і кусково-диференційовних функцій , яка рівномірно збігається при до функції 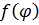, і розглянемо задачу Діріхле

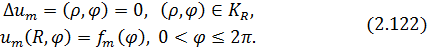
Згідно з доведеним вище розв’язком задачі (2.122) набирає вигляду

Оскільки послідовність функцій рівномірно збігається при , то вона рівномірно збігається всюди в до неперервної функції , причому . Покажемо, що функція представляється рядом (2.118), який, згідно з доведеним, є гармонічною функцією при .

Нехай і – коефіцієнти ряду Фур'є функції . Тоді внаслідок рівномірної збіжності послідовності функцій , для всякого і досить великого буде , тобто для всіх

Беручи до уваги останні нерівності й (2.118), дістанемо

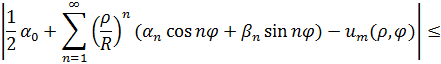
а отже, гранична функція при набирає вигляду(2.13).

Теорему доведено.

Дата добавления: 2017-02-01