Рівняння вільних коливань струни

Застосування методу відокремлених змінних до розв’язування рівнянь гіперболічного типу.

Рівняння гіперболічного типу, до яких найчастіше призводять фізичні задачі, пов’язані з процесами коливання струни, мембрани, газу, електромагнітних коливань. Характерною особливістю згаданих процесів є скінченна швидкість їх поширення.

Ряди Фур’є найчастіше використовують для розв’язування задач математичної фізики. Розглянемо задачу про малі коливання однорідної струни довжини l, закріпленої на кінцях. Рівняння коливань для однорідної струни має вигляд

(2.1)

з початковими умовами

(2.2)

Та крайовими умовами

де – переміщення струни; – величина, що залежить від зведеної (до лінії) густини матеріалу і сили натягу струни .

Згідно з методом Фур’є будемо шукати нетривіальні (не рівні тотожно нулеві) частинні розв’язки рівняння (2.1), які задовольняють крайові умови (2.3), у вигляді добутку двох функцій, кожна з яких залежить тільки від однієї змінної

Підставимо (2.4) в рівняння (2.1) і отримаємо

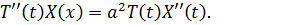
Або

Ліва частина рівняння (5) залежить лише від , а права – тільки від звідси висновок, що обидва відношення дорівнюють сталій:

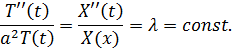
Отримаємо два звичайні диференціальні рівняння

Таким чином, для визначення функції 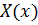одержали крайову задачу Штурма-Ліувілля для рівняння (7)із крайовими умовами:

Таким чином, ми отримали наступну задачу: знайти такі значення параметра , при яких існують нетривіальні розв’язки (2.7), що задовольняють умовам (2.8).

Ті значення , при яких задача (2.7)-(2.8) має нетривіальні розв’язки, називаються власними числами або власними значеннями, а самі ці розв’язки – власними функціями.

Знайдемо власні числа та власні функції задачі (2.7)-(2.8).

Потрібно розглянути три випадки: , та .

1) Якщо , то характеристичне рівняння для рівняння (2.7) має вигляд , а тоді загальний розв’язок рівняння (2.7) буде

З (КУ) (2.8) отримаємо систему для знаходження та :

Визначник цієї системи не дорівнює нулю, а значить, .

Отримали – тривіальний розв’язок.

2) Якщо , то загальний розв’язок рівняння (2.7) є . З (КУ) (8) отримаємо

Звідси , а значить, .

3) . Позначимо тоді характеристичне рівняння прийме вигляд , а загальним розв’язком рівняння (2.7) буде

і знайдемо з (КУ) (2.7):

З першого рівняння , а з другого . Ми шукаємо нетривіальний розв’язок, тому а значить, 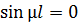, тобто 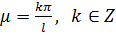,. Отже, нетривіальні розв’язки задачі (2.7)-(2.8) можливі лише при

Цим власним числам 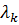відповідають власні функції

Знайдемо тепер функції з рівняння (2.6):

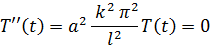
Характеристичне рівняння знову має уявні корені 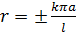а тому загальний розв’язок рівняння (2.6) є

де та – довільні числа.

Таким чином, функції

задовольняють рівнянню (2.1) та (КУ) (2.3). Рівняння (2.1) лінійне і однорідне, а тому розв’язком цього рівняння буде всяка скінченна сума. Але розв’язком рівняння (2.1) буде і ряд

якщо він збігається і його можна двічі диференціювати по x та t. Кожний доданок ряду (2.9) задовольняє (КУ) (2.3), тому цим умовам буде задовольняти і сума ряду, тобто функція . Залишається підібрати коефіцієнти та так, щоб виконувались (ПУ) (2.2):

Формули (2.10) є розкладами в ряди Фур’є по синусах відповідно функцій та в інтервалі . Ці коефіцієнти знаходяться за формулами

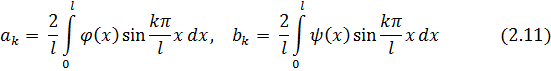
Коефіцієнти (2.11) підставимо в (2.9) і отримаємо розв’язок змішаної задачі (1), (2), (3).

Якщо позначити то розв’язок (2.9) можна записати у вигляді

Кожен член цього ряду є гармонічна функція з амплітудою , з частотою і фазою . В точках амплітуда коливань -ої гармоніки дорівнює нулеві. Ці точки називаються вузлами -ої гармоніки.

А в точках які називають збурення,амплітуда -ої гармоніки досягає найбільшого значення.

Зауваження 1. При розв`язанні крайової задачі методом відокремлення змінних суттєва однорідність граничних умов, причому ці умови можуть бути не тільки першого типу

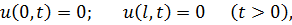
а й другого

чи третього (змішаного) типу

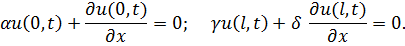
Якщо граничні умови ненульові, то заміною змінних задачу треба попередньо звести до випадку однорідних (нульових) граничних умов.

Наприклад, якщо задано граничні умови

то використовується заміна

Тут – довільно задана функція, що задовольняє вказані граничні умови, зокрема, можна покласти – нова шукана функція, що задовольняє однорідні граничні умови.

Звичайно, диференціальне рівняння і початкові умови при цьому дещо ускладнюються.

Зауваження 2. Якщо треба розв`язати крайову задачу для неоднорідного ДРЧП з однорідними граничними умовами, то її розв`язок шукають у вигляді функціонального ряду за власними функціями 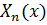відповідної однорідної задачі (метод розкладання за власними функціями). Можливий також інший підхід: якщо для неоднорідного ДРЧП, яким-небудь способом знайти частинний розв`язок , що задовольняє однорідні граничні і однорідні початкові умови, то введення нової шуканої функції за формулою приводить до відповідної крайової задачі для однорідного ДРЧП.

Для обґрунтування методу Фур’є необхідно показати, що ряди, у формі яких представлені розв’язки крайових задач, збігаються рівномірно і їх можна двічі почленно диференціювати. Щоб довести даний факт найзручніше скористатися ознакою Вейэштрасса [5,132].

Теорема 1. Нехай:

а) функція два рази неперервно диференційована на відрізку [ 0,l ] і має кузково-неперервну третю похідну (неперервну кусково-гладку другу похідну), а також задовольняє умови

б) функція неперервно диференційована на [ 0,l ], має кусково-неперервну другу похідну (неперервну кусково-гладку першу похідну) і задовольняє умови

Тоді функція – сума ряду (2.12) має неперервні другі похідні і задовольняє рівняння (2.1), умови (2.2) та (2.3).

Доведення. Інтегруючи частинами інтеграли у виразах для коефіцієнтів і з урахуванням умови (2.13) і (2.14), одержимо

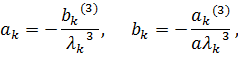
Підставляючи одержані вирази у ряд (2.12), маємо

Цей ряд мажорується збіжним числовим рядом

і тому збігається рівномірно і абсолютно в області .

Продиференціюємо почленно ряд (2.15) два рази по x, t,

Ці ряди мажоруються числовим рядом

З нерівності випливають такі нерівності:

третя похідна від функції і друга похідна від функції інтегровані з квадратом на проміжку [0,l] і тому збіжні ряди

Тоді, ґрунтуючись на нерівностях (2.18), можна стверджувати, що збігається ряд (17). Збіжність ряду (2.17) забезпечує рівномірну збіжність рядів (2.16) в області ..

Внаслідок рівномірної збіжності рядів (2.16) і (2.11), а також виконання умов (2.13) і (2.14), можна ці ряди перетворювати і, відповідно, сума ряду (2.15) є розв’язком задачі (2.1) – (2.3). Теорему доведено.

Зауваження. Умови (13) і (14) можна замінити умовами періодичності і непарності відповідних функцій.

Дата добавления: 2017-02-01